A long wire carrying a current i is bent to form a plane angle. The magnitude of magnetic field at height d, above the point of bending
√2μ0i4πd
3√2μ0i4πd
5√2μ0i4πd
7√2μ0i4πd
The correct Answer is:A
To solve the problem of finding the magnitude of the magnetic field at height d above the point of bending of a long wire carrying a current i that is bent to form a plane angle, we can follow these steps:
Step 1: Understand the Configuration
We have a long wire bent at a 90-degree angle. The current i flows through the wire, and we need to find the magnetic field at a point located at a height d above the point where the wire is bent.
Step 2: Identify the Sections of the Wire
The wire can be considered as two semi-infinite straight wires:
1. One part of the wire extends vertically (let's call it wire A).
2. The other part extends horizontally (let's call it wire B).
Step 3: Use the Formula for Magnetic Field Due to a Semi-Infinite Wire
The magnetic field B at a distance r from a straight wire carrying current I is given by the formula:
\(
B = \frac{\mu_0 I}{4 \pi r}
\)
where μ₀ is the permeability of free space.
Step 4: Calculate the Magnetic Field from Wire A
For wire A (the vertical wire), the distance from the point of interest (height d) to the wire is d. Thus, the magnetic field BA due to wire A at the point above the bending is:
\(
B_A = \frac{\mu_0 i}{4 \pi d}
\)
The direction of the magnetic field due to wire A can be determined using the right-hand rule. If the current flows upwards, the magnetic field will circulate around the wire, pointing towards the right (let's assume this is in the positive x-direction).
Step 5: Calculate the Magnetic Field from Wire B
For wire B (the horizontal wire), the distance from the point of interest to the wire is also d. Thus, the magnetic field BB due to wire B at the same point is:
\(
B_B = \frac{\mu_0 i}{4 \pi d}
\)
The direction of the magnetic field due to wire B can also be determined using the right-hand rule. If the current flows to the right, the magnetic field will point upwards (in the positive z-direction).
Step 6: Combine the Magnetic Fields
Since the magnetic fields from wire A and wire B are perpendicular to each other (one in the x-direction and one in the z-direction), we can use the Pythagorean theorem to find the resultant magnetic field B≠t:
\(
B_{net} = \sqrt{B_A^2 + B_B^2}
\)
Substituting the values of BA and BB:
\(
B_{net} = \sqrt{\left(\frac{\mu_0 i}{4 \pi d}\right)^2 + \left(\frac{\mu_0 i}{4 \pi d}\right)^2}
\)
\(
B_{net} = \sqrt{2 \left(\frac{\mu_0 i}{4 \pi d}\right)^2} = \frac{\mu_0 i}{4 \pi d} \sqrt{2}
\)
Step 7: Final Result
Thus, the magnitude of the magnetic field at height d above the point of bending is:
\(
B_{net} = \frac{\mu_0 i \sqrt{2}}{4 \pi d}
\)
We have a long wire bent at a 90-degree angle. The current i flows through the wire, and we need to find the magnetic field at a point located at a height d above the point where the wire is bent.
The wire can be considered as two semi-infinite straight wires:
1. One part of the wire extends vertically (let's call it wire A).
2. The other part extends horizontally (let's call it wire B).
The magnetic field B at a distance r from a straight wire carrying current I is given by the formula:
\(
B = \frac{\mu_0 I}{4 \pi r}
\)
where μ₀ is the permeability of free space.
For wire A (the vertical wire), the distance from the point of interest (height d) to the wire is d. Thus, the magnetic field BA due to wire A at the point above the bending is:
\(
B_A = \frac{\mu_0 i}{4 \pi d}
\)
The direction of the magnetic field due to wire A can be determined using the right-hand rule. If the current flows upwards, the magnetic field will circulate around the wire, pointing towards the right (let's assume this is in the positive x-direction).
For wire B (the horizontal wire), the distance from the point of interest to the wire is also d. Thus, the magnetic field BB due to wire B at the same point is:
\(
B_B = \frac{\mu_0 i}{4 \pi d}
\)
The direction of the magnetic field due to wire B can also be determined using the right-hand rule. If the current flows to the right, the magnetic field will point upwards (in the positive z-direction).
Since the magnetic fields from wire A and wire B are perpendicular to each other (one in the x-direction and one in the z-direction), we can use the Pythagorean theorem to find the resultant magnetic field B≠t:
\(
B_{net} = \sqrt{B_A^2 + B_B^2}
\)
Substituting the values of BA and BB:
\(
B_{net} = \sqrt{\left(\frac{\mu_0 i}{4 \pi d}\right)^2 + \left(\frac{\mu_0 i}{4 \pi d}\right)^2}
\)
\(
B_{net} = \sqrt{2 \left(\frac{\mu_0 i}{4 \pi d}\right)^2} = \frac{\mu_0 i}{4 \pi d} \sqrt{2}
\)
Thus, the magnitude of the magnetic field at height d above the point of bending is:
\(
B_{net} = \frac{\mu_0 i \sqrt{2}}{4 \pi d}
\)
Topper's Solved these Questions
Similar Questions
Alongwirecarry∈gacurrentiisbent→formapla≠∠α. F∈dthemag≠ticfieldBatap∮onthebisec→rofthis∠situatedatadistancexomthevertex.
View SolutionFind magnitude and direction of magnetic field at point P in the following cases.
(a)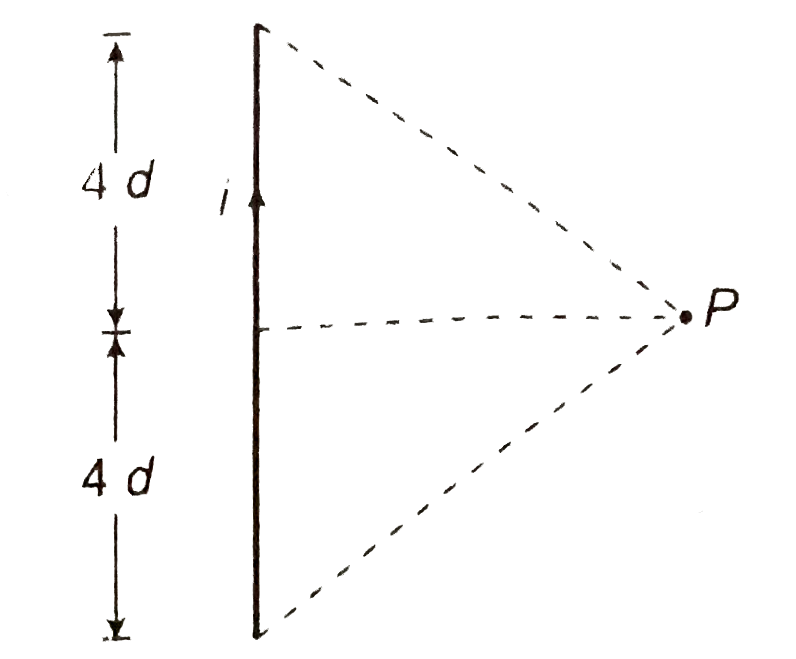
(b)
P is the centre of square.
(c)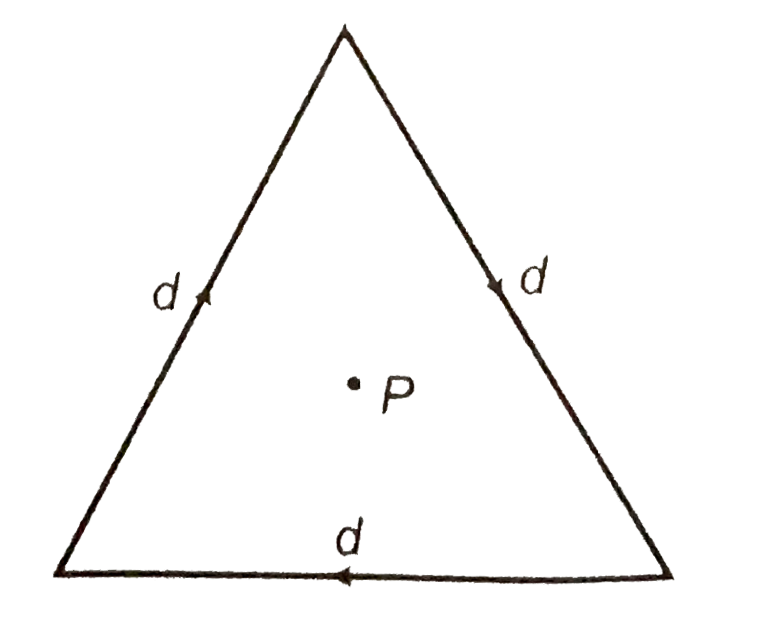
P is the centre of equilateral triangle.
(d)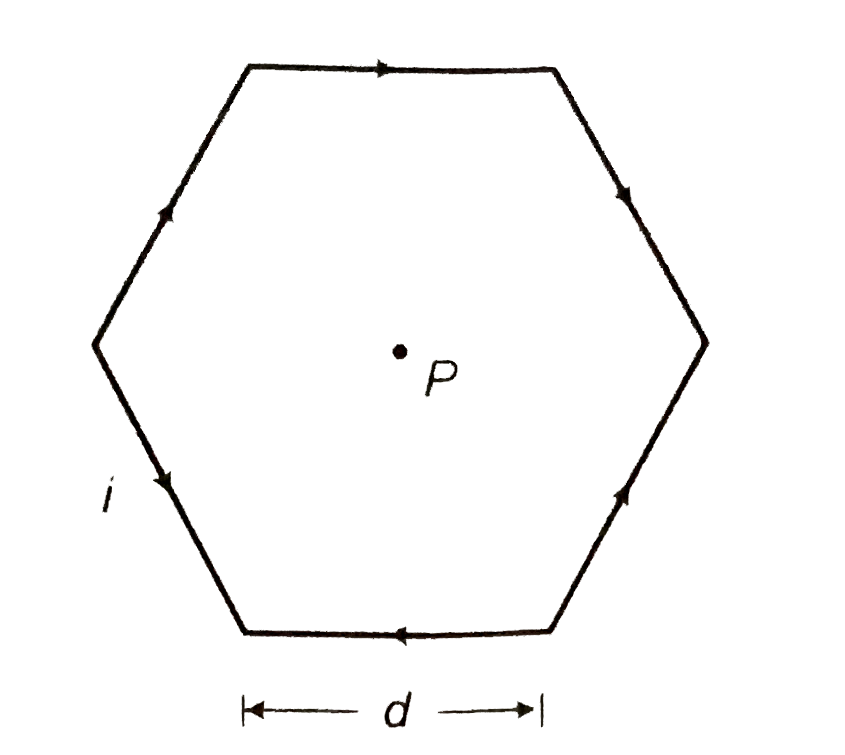
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)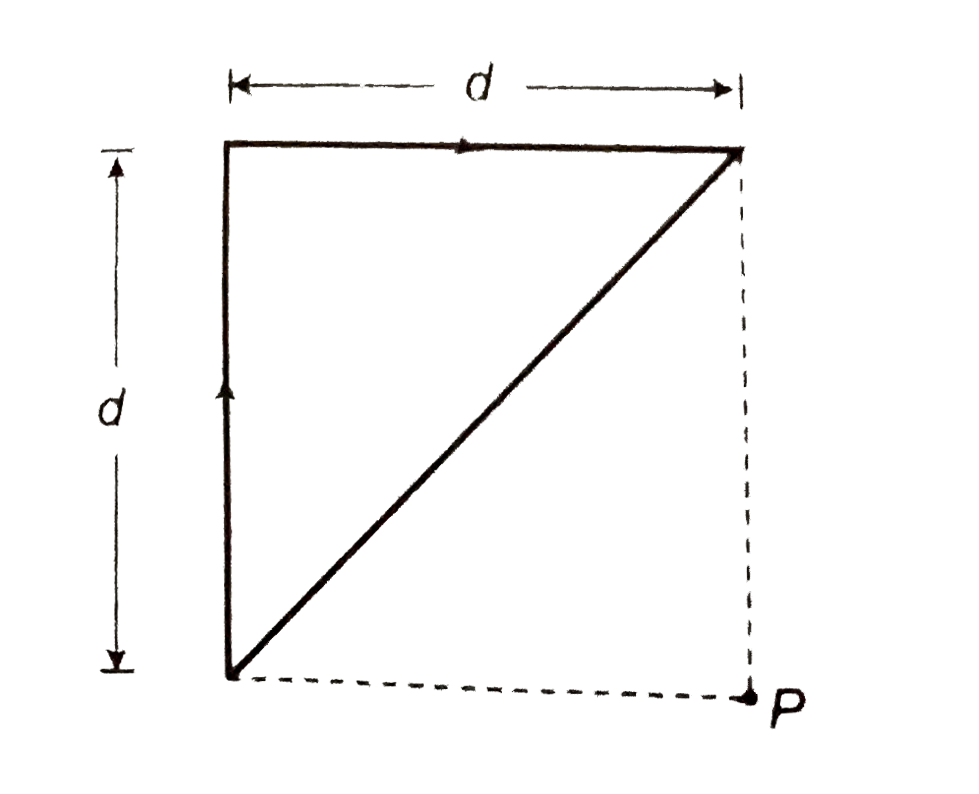
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.
View Solution
Knowledge Check
A long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
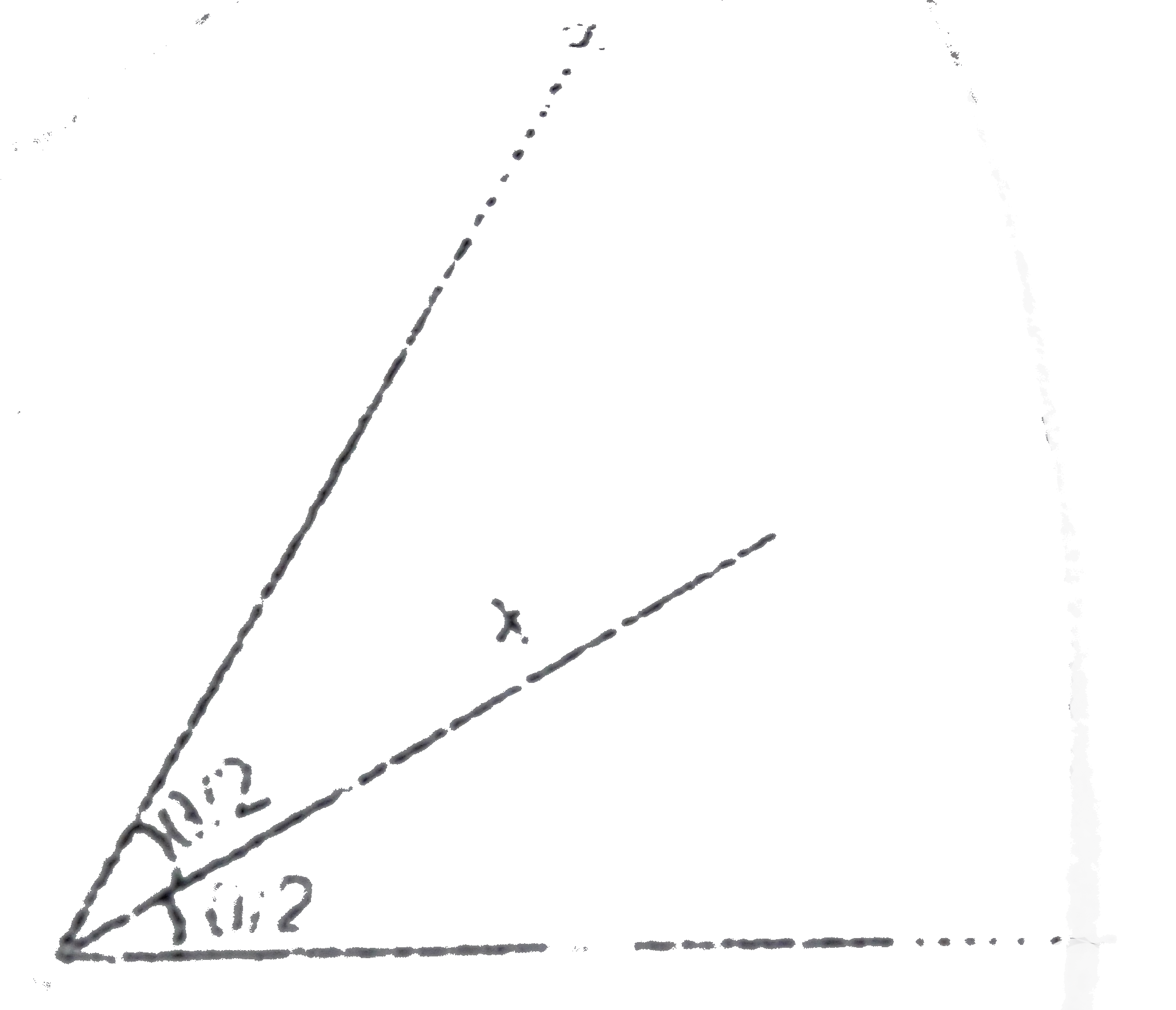 Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙
Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙A wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
Aπμ0ILBμ0I2LC2πμ0ILDμ0I2πLA wire of length L carrying a current I is bent into a circle. The magnitude of the magneitc field at the centre of the circle is
Aπμ0ILBμ0I2LC2πμ0ILDμ0I2πL
A conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
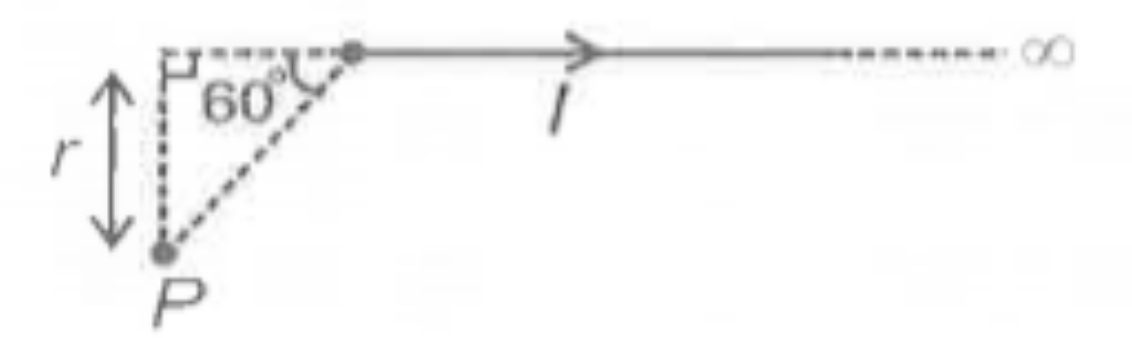
View SolutionA long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.

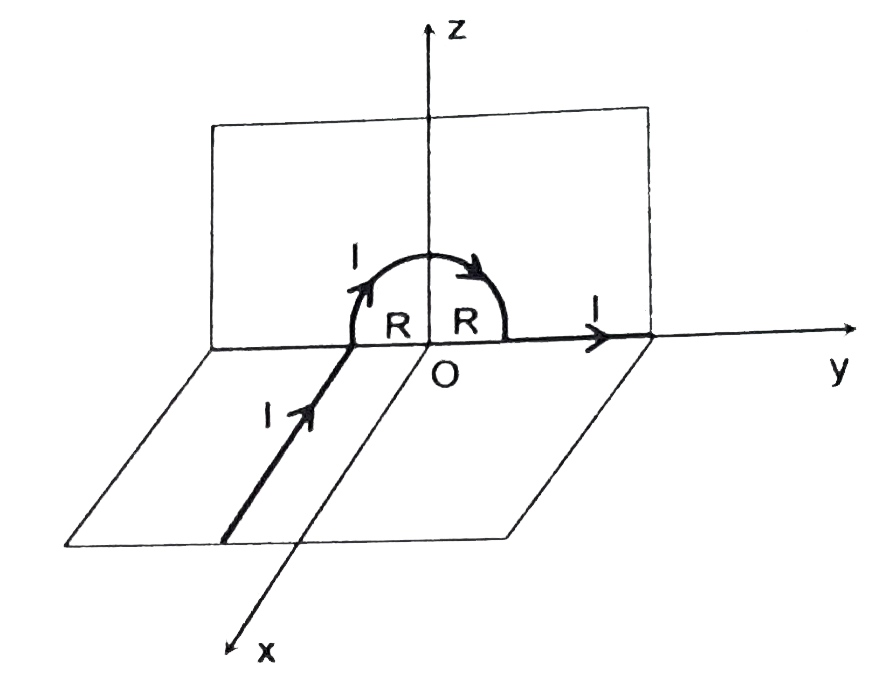
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
View SolutionA long wire carrying a current i=2A is bent at right angles . The magnetic field lying on a perpendicular normal to the plane of the wire draw through the point of bending at distance 1 m form it is ………….Tesla.
View SolutionA long conducting wire carrying a current I is bent at 120∘( see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is
(μ0 is the permeability of free space)

View Solution

