The magnetic field at O is

μ0I2R√(14+1π2)
μ0I2R√(12+1π2)
μ0IR√(14+1π2)
μ0IR√(14+1π)
The correct Answer is:A
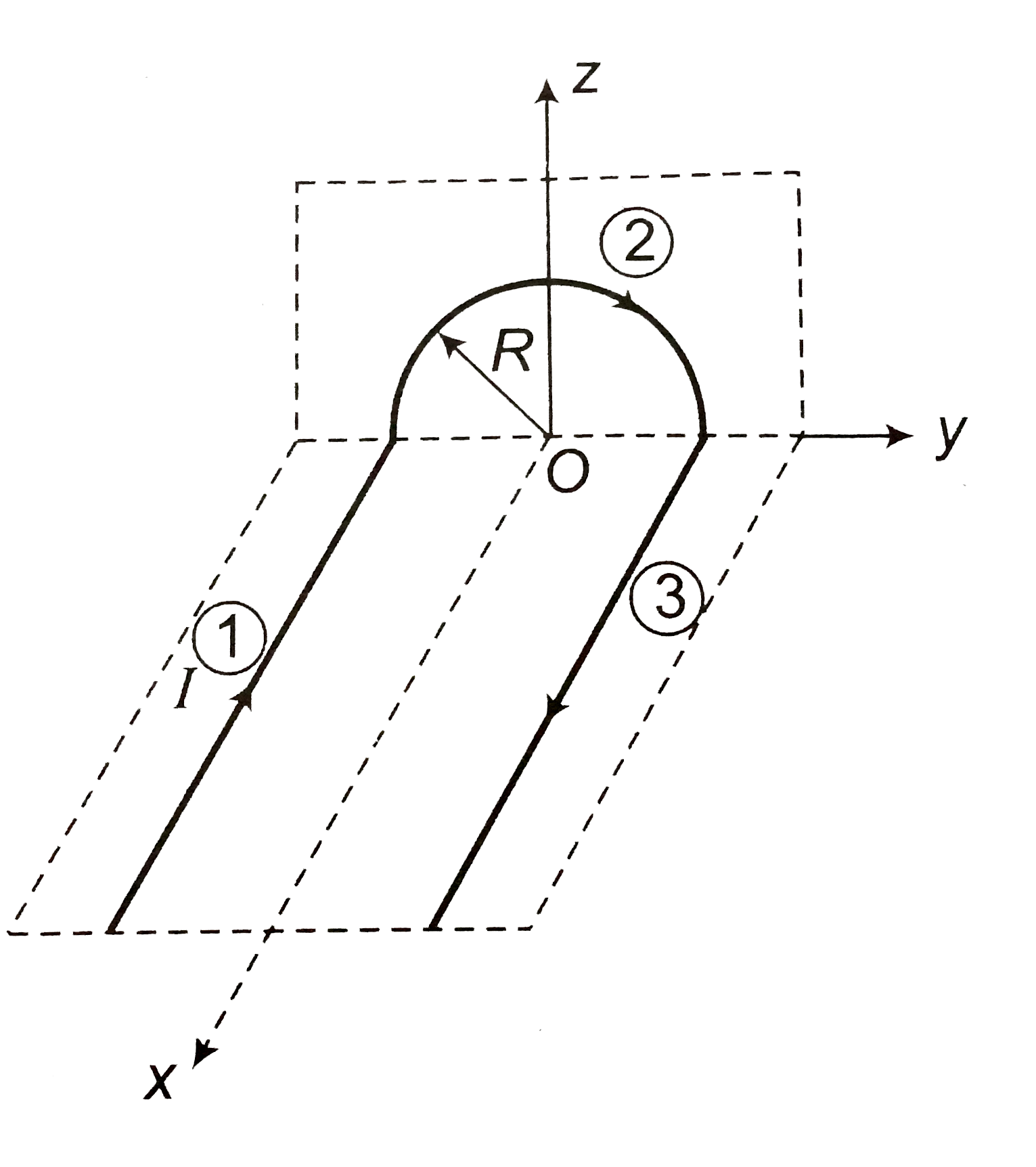
Magnetic field at O:
Wire ① is in x−y plane
B1=μ0I4πR, along −zaxis
Wire ② is in y−z plane
B2=μ0I4R, along −xaxis
Wire ③ is in x−y plane
B3=μ0I4πR, along −zaxis
→B0=−(B1+B2)ˆk−B2ˆi
∣∣→Bo∣∣=√(B1+B3)2+B22=√(μ0I2πR)2+(μ0I4R)2
=μ0I2R√1π2+14
Topper's Solved these Questions
Similar Questions
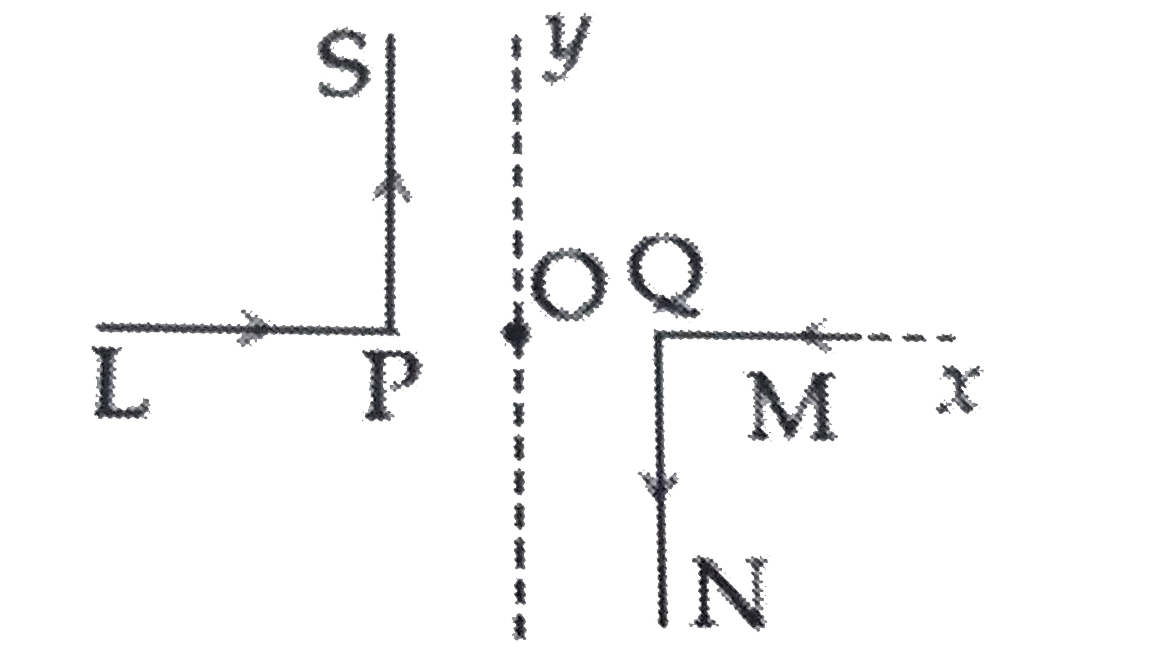
As shown in the figure two infinitely long, identical wires are bent by 90∘ and placed in such a way that the segments LP and QM are along the x-axis , while segments PS and QN are parallel to the Y-axis If OP=OQ=4 cm ,and the magnitude of the magnetic field at O is 10−4 T, and the magnitude of the current in each wire and the direction of the magnetic field at O will be
(μo=4π×10−7NA−2):
View SolutionA loop ABCD has current I = 10 A , as shown in the figure . AD and BC are circular arcs with centre at O, for both . The magnetic field at point O is

View Solution
Knowledge Check
the unit vector ˆi,ˆj and ˆk are as shown below. What will be the magnetic field at O in the following figure ?
 Aμ04πia(2−π2)ˆjBμ04πia(2+π2)ˆjCμ04πia(2+π2)ˆiDμ04πia(2+π2)ˆk
Aμ04πia(2−π2)ˆjBμ04πia(2+π2)ˆjCμ04πia(2+π2)ˆiDμ04πia(2+π2)ˆkThe magnetic field at O due to current in the infinite wire forming a loop as a shown in Fig.
 Aμ0I2πd(cosϕ1+cosϕ2)Bμ04π2Id(tanθ1+tanθ2)Cμ04πId(sinϕ1+sinϕ2)Dμ04πId(cosθ1+cosθ2)
Aμ0I2πd(cosϕ1+cosϕ2)Bμ04π2Id(tanθ1+tanθ2)Cμ04πId(sinϕ1+sinϕ2)Dμ04πId(cosθ1+cosθ2)The unit vectors ˆi,ˆj and ˆk are as shown below. What will be the magnetic field at O in the following figure
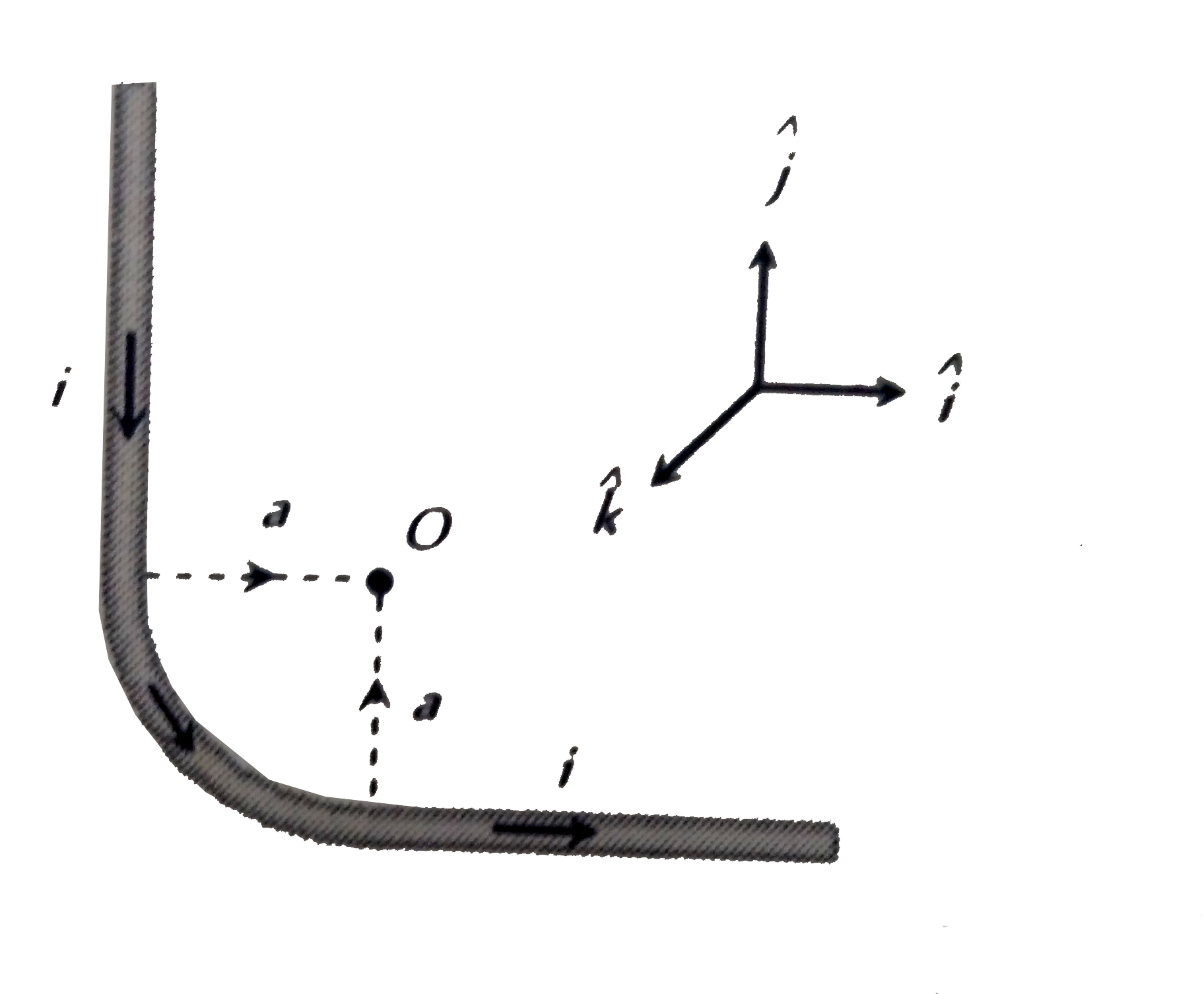 Aμ04πia(2−π2)ˆjBμ04πia(2+π2)ˆjCμ04πia(2+π2)ˆiDμ04πia(2+π2)ˆk
Aμ04πia(2−π2)ˆjBμ04πia(2+π2)ˆjCμ04πia(2+π2)ˆiDμ04πia(2+π2)ˆk
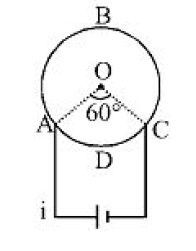
A cell is connected between the points A and C of a circular conductor ABCD of centre 'O'.∠AOC=60∘. IfB1andB2 are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio B1B2, is
View SolutionIn the given figure the magnitude of magnetic field at O is ( all three wires are quarter circular ares )

View SolutionTwo small magnets of each of magnetic moment M0 is placed parallel to each other (show in figure). The magnetic field at point O is

View SolutionA cell is connected between the points A and Cofa circular conductor ABCDA of centre O. ∠AOC=60∘. If B1, and B2, are the magnitudes of the magnetic fields at O due to currents in ABC and ADC respectively, the ratio B1/B2, is
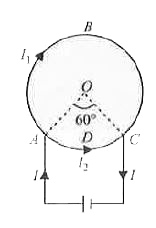
View SolutionFind magnetic field at O.
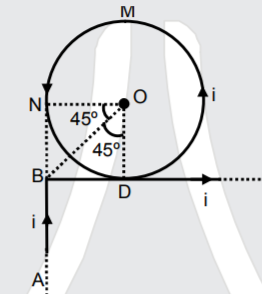
View Solution

