A mass of 2kg suspended by string of mass 6kg. A wave of wavelength 6 cm is produced at bottom of string. Wavelength of wave at top end of string will be
6 cm
18 cm
12 cm
24 cm
The correct Answer is:C
To solve the problem, we need to determine the wavelength of the wave at the top end of the string given the wavelength at the bottom end and the relationship between tension and wave speed in a string.
1. Identify Given Values:
- Mass of the suspended object (m1) = 2 kg
- Mass of the string (m2) = 6 kg
- Wavelength at the bottom of the string (λ1) = 6 cm
2. Calculate Tension at the Bottom of the String (T1):
- The tension at the bottom of the string (T1) is equal to the weight of the suspended mass.
T1=m1⋅g=2kg⋅g
(where g is the acceleration due to gravity, approximately 9.81m/s2, but we can keep it as g for our calculations).
3. Calculate Tension at the Top of the String (T2):
- The tension at the top of the string (T2) is equal to the weight of the suspended mass plus the weight of the string.
T2=(m1+m2)⋅g=(2kg+6kg)⋅g=8kg⋅g
4. Relate Wave Speeds and Wavelengths:
- The wave speed in a string is given by the formula:
v=√Tμ
where T is the tension and μ is the mass per unit length of the string. Since we are not given the mass per unit length, we can use the relationship between the wave speeds and wavelengths:
v1v2=λ1λ2
where v1 and v2 are the wave speeds at the bottom and top of the string, respectively.
5. Express Wave Speeds in Terms of Tension:
- Since the wave speed is proportional to the square root of tension, we can write:
v1v2=√T1T2
6. Substituting Values:
- From the previous steps:
v1v2=√2g8g=√28=√14=12
7. Relate Wavelengths:
- Now substituting this into the wavelength relationship:
λ1λ2=12
Rearranging gives:
λ2=λ1⋅2
8. Calculate Wavelength at the Top of the String:
- Substitute λ1 = 6 cm:
λ2=6cm⋅2=12cm
Final Answer:
The wavelength of the wave at the top end of the string is 12 cm.
- Mass of the suspended object (m1) = 2 kg
- Mass of the string (m2) = 6 kg
- Wavelength at the bottom of the string (λ1) = 6 cm
- The tension at the bottom of the string (T1) is equal to the weight of the suspended mass.
T1=m1⋅g=2kg⋅g
(where g is the acceleration due to gravity, approximately 9.81m/s2, but we can keep it as g for our calculations).
- The tension at the top of the string (T2) is equal to the weight of the suspended mass plus the weight of the string.
T2=(m1+m2)⋅g=(2kg+6kg)⋅g=8kg⋅g
- The wave speed in a string is given by the formula:
v=√Tμ
where T is the tension and μ is the mass per unit length of the string. Since we are not given the mass per unit length, we can use the relationship between the wave speeds and wavelengths:
v1v2=λ1λ2
where v1 and v2 are the wave speeds at the bottom and top of the string, respectively.
- Since the wave speed is proportional to the square root of tension, we can write:
v1v2=√T1T2
- From the previous steps:
v1v2=√2g8g=√28=√14=12
- Now substituting this into the wavelength relationship:
λ1λ2=12
Rearranging gives:
λ2=λ1⋅2
- Substitute λ1 = 6 cm:
λ2=6cm⋅2=12cm
The wavelength of the wave at the top end of the string is 12 cm.
Topper's Solved these Questions
Similar Questions
A block of mass M=2kg is suspended from a string AB of mass 6kg as shown in figure. A transverse wave pulse of wavelength λ0 is produced at point B. find its wavelength while reaching at point A.
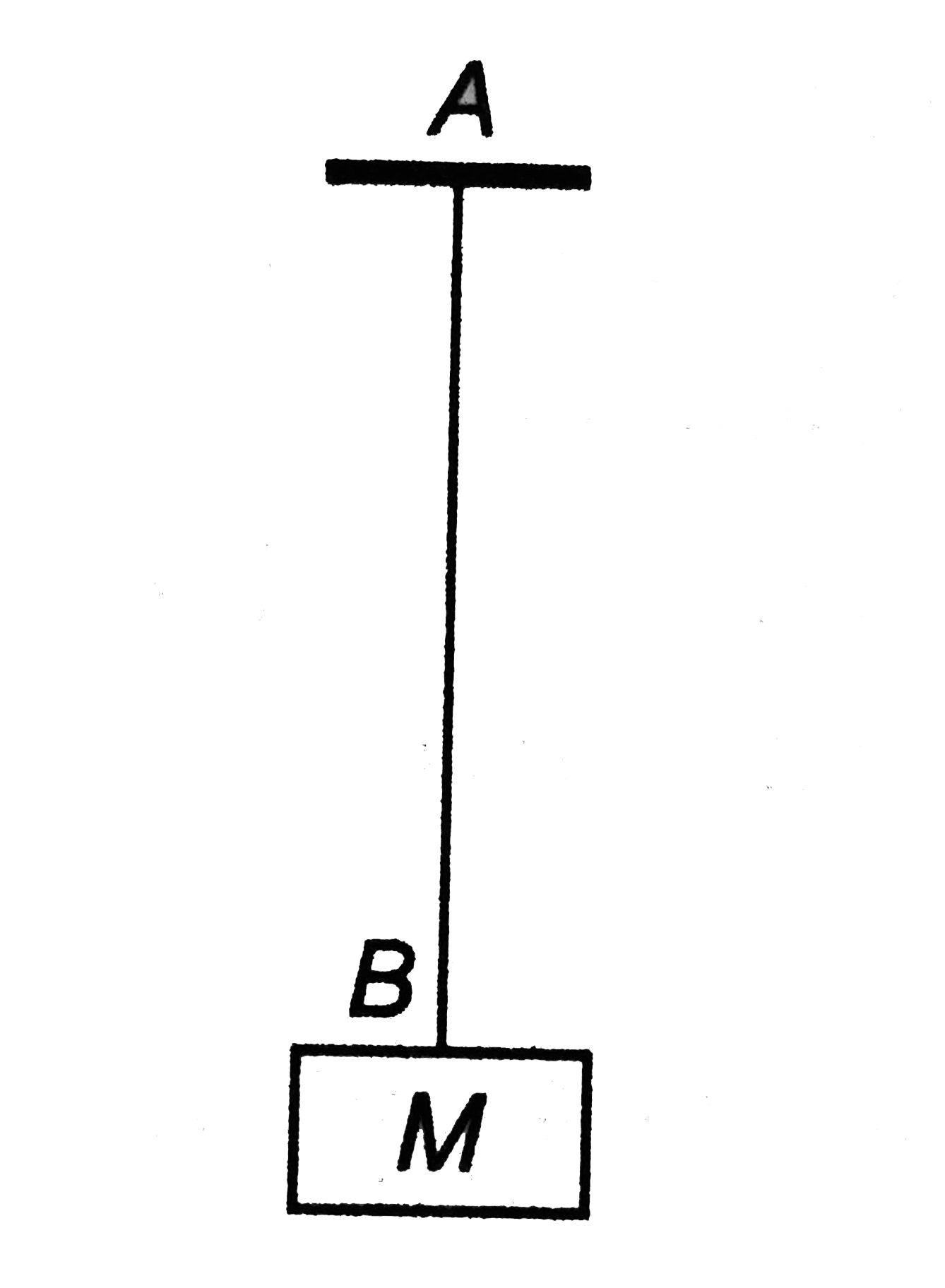
View SolutionA uniform rope of length 12m and mass 6kg hangs vertically from a rigid support. A block of mass 2kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06m is produced at the lower end of the rope. What is the wavelength of the pulse whwn it reaches the top of the rope?
View Solution
Knowledge Check
A string of mass 0.250 kg is under a tension of 2 N. The length of the stretched string is 2 m. A transverse wave disturbance starts at one end of the string . How long will the disturbance take to reach the other end ?
A1,5 sB1.5 sC1 sD0.5 sA mass of 1kg is suspended by a string A. Another string C is connected to its lower end (see figure). If a sudden jerk is given to C, then
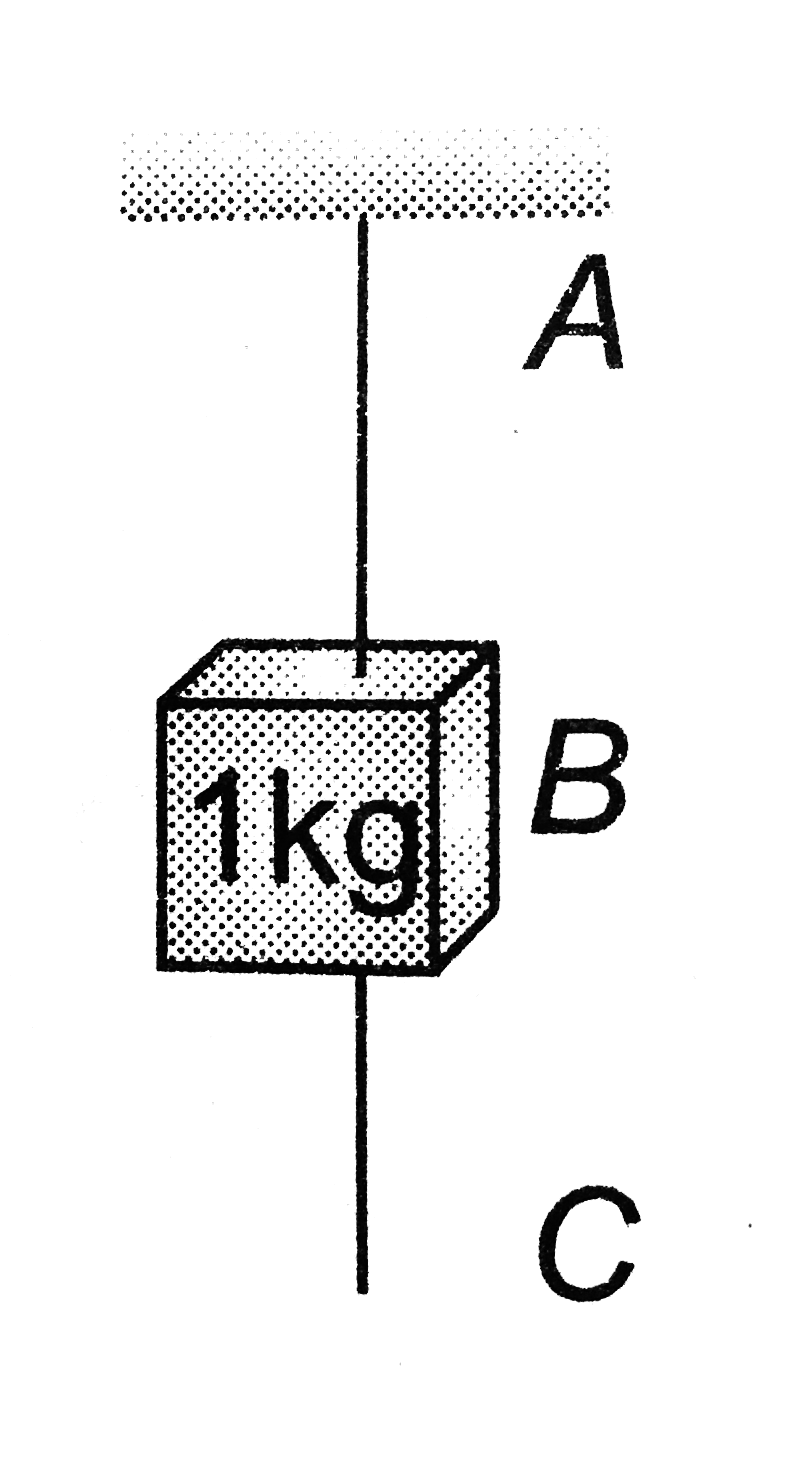 AThe portion AB of the string will breakBThe portion BC of the string will breakCNone of the string will breakDThe mass will start rotating
AThe portion AB of the string will breakBThe portion BC of the string will breakCNone of the string will breakDThe mass will start rotatingA standing wave is produced on a string on a string clamped at one end and free at the other. The length of the string
Amust be an integral multiple λ4Bmust be an integral multiple of λ2Cmust be an integral multiple of λDmay be an integral multiple of λ2
A block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.

View SolutionIn a string, stationary waves are produced by
View SolutionA standing wave with a number of loops is produced in a stringe fiex at both ends. In this case
View SolutionA mass m is suspended from the ceiling by a string with variable linear mass density (μ).A wave pulse is produced at the top of an oscillator which travels from top to bottom with constant wave speed. (x axis is positive downwards). Then.
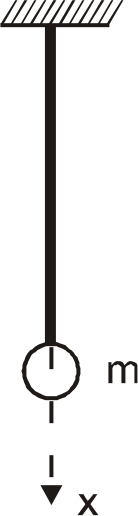
View Solution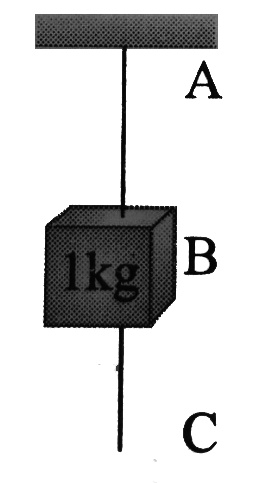
A mass of 1 kg is suspended by a string A. another string C is connected to its lower end (see figure). If the string C is stretched slowly, then
View Solution

