A standing wave with a number of loops is produced in a stringe fiex at both ends. In this case
all particles vibrate in phase
particles at all antinodes vibrate in phase
particles at alternate antinodes vibrate in phase
particles between two consecutive antinodes vibrate in phase
The correct Answer is:C
In standing wave , all particles within one loop are in the same phase but particles in adjacent loops are 180∘ out of phase. Hence particles at alternate antinodes vibrate in phase .
Topper's Solved these Questions
- STATIONARY WAVESBook:MARVEL PUBLICATIONChapter:STATIONARY WAVESExercise:MULTIPLE CHOICE QUESTIONS (HIGHER LEVEL )
Explore 7 Videos
- STATIONARY WAVESBook:MARVEL PUBLICATIONChapter:STATIONARY WAVESExercise:MULTIPLE CHOICE QUESTIONS ( STANDARD LEVEL )
Explore 65 Videos
- SEMICONDUCTORS Book:MARVEL PUBLICATIONChapter:SEMICONDUCTORS Exercise:MCQs
Explore 261 Videos
- SURFACE TENSION Book:MARVEL PUBLICATIONChapter:SURFACE TENSION Exercise:MULTIPLE CHOICE QUESTIONS . (TEST YOUR GRASP )
Explore 10 Videos
Similar Questions
A string 1 m long is fixed at one end. The other end is moved up and down with frequency 20 Hz. Due to this, a stationary wave with four complete loops, gets produced on the string. Find the speed of the progressive wave which produces the stationary wave. [Note: Remember that the moving end is a antinode.]
View SolutionThe equation of a standing wave, produced on a string fixed at both ends, is y=(0.4cm)sin[(0.314cm−1)x]cos[(600πs−1)t] What could be the smallest length of the string ?
View Solution
Knowledge Check
Four standing wave segments, or loops, are observed on a string fixed at both ends as it vibrates at a frequency of 140 Hz. What is the fundamental frequency of the string?
A23 HzB28 HzC35 HzD47 HzStationary waves are produced in 10 m long stretched string. If the string vibrates in 5 segments and wave velocity 20 m/s then the frequency is :-
A5HzB10 HzC2 HzD4 HzA stationary wave y=0.4sin2π40cos100πt is produced in string fixced of both ends. The minimum possible length of the string is given by
A10mB20√2mC20mD28m
Standing waves can be produced
View SolutionIn a standing wave on a string.
View SolutionStanding waves can be produced in
View SolutionDe-Broglie hypothesized that material particles have wave like properties. Figure shows a small particle in a box. The particle simply bounces back and forth at constant speed. As particles also have wave like properties it can be considered to be a wave reflecting back and forth from the ends of the box. The reflections will create a standing wave analogous to standing wave on a string tied at both ends. Since a standing wave confined to a region can have only selected wavelength, momentum of the particle is quantized. We can safely assume that such a particle only has kinetic energy. This energy must also be quantized.
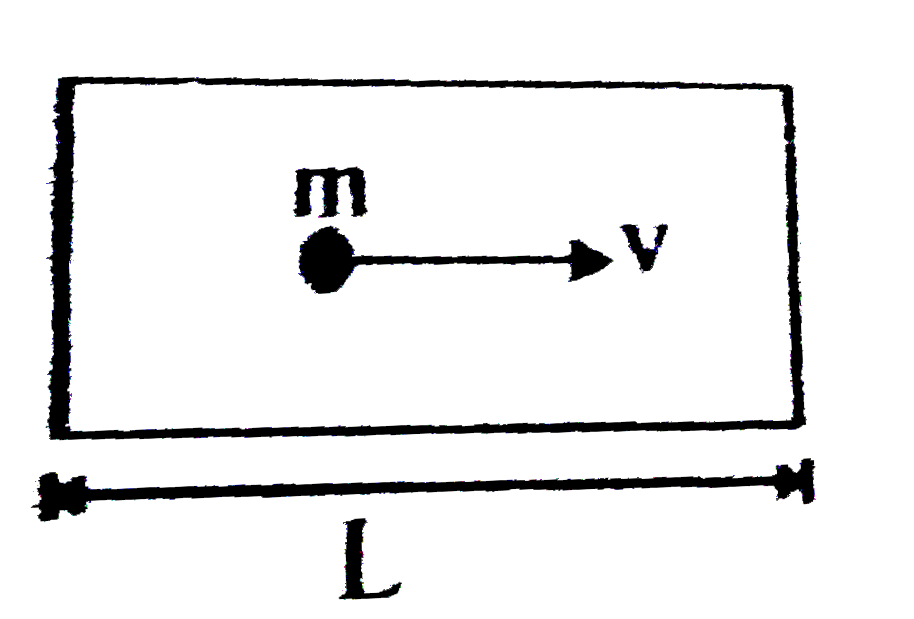
What is momentum of particle in n^(th) mode of standing wave ?
View SolutionA standing wave is produced on a string on a string clamped at one end and free at the other. The length of the string
View Solution

