The left block in filgure collides inelastically with the right block and sticks to it. Find the amplitude of the resulting simple harmonic motion.
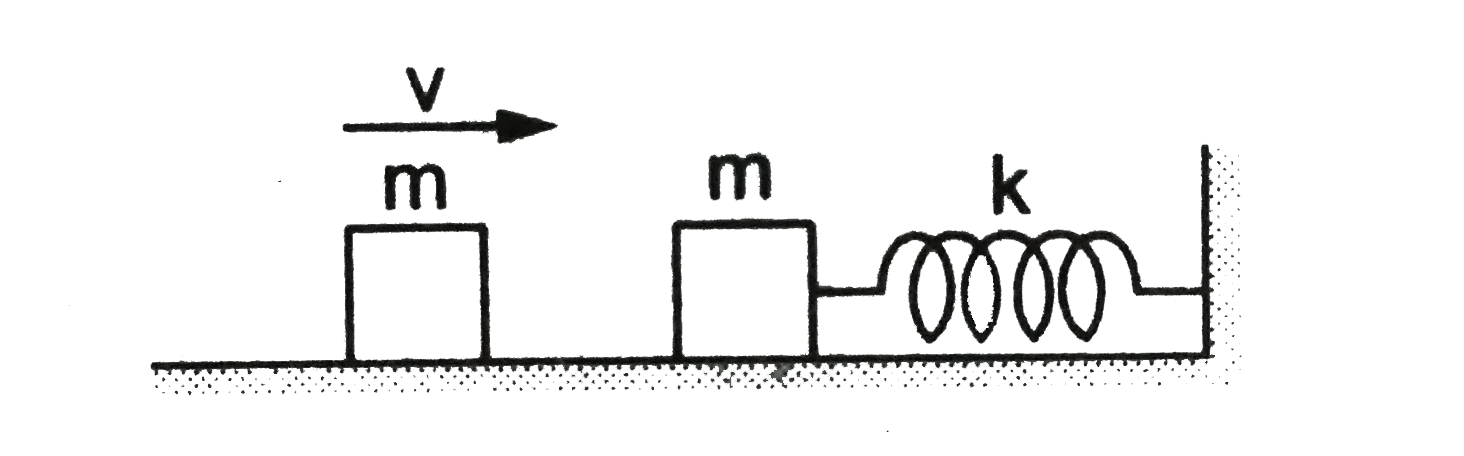
Assuming the collision to last for a small interval only, we can apply the principle of conservation momentum. The common velocity after the collision is v2. The kinectic energy =12(2m)(v2)2=14mv2. This is also the total energy of viberation as the spring isunstretched at this moment. If the amplitude is A, the total energy cen also be written as 12kA2. Thus,
12kA2=14mv2, giving A=√m2kv.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Solved Miscellaneous Problems
9 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise
24 Videos
- SEMICONDUCTORSBOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-3
30 Videos
Similar Questions
The left block in figure collides inelastically with the right block and sticks to it. Find the amplitude of the resulting simple harmonic motion.

View SolutionThe left block in figure collides inelastically with the right block and striks to it. Find the amplitude of the resulting simple harmonic motion
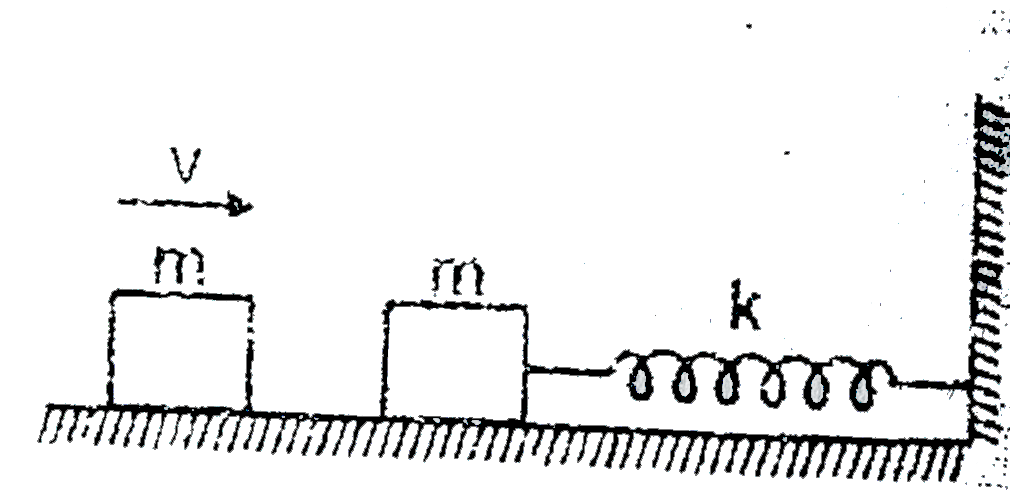
View Solution
Knowledge Check
A block is attached to a horizontal spring and oscillates back and forth on f frictionless horizontal surface at a frequency of 3.00Hz. The amplitude of the motion is 5.08×10−2m. At the point where the block has its maximum speed, it suddenly splits into two identical parts, only one part remaining attached to the spring. What is the amplitude and the frequency of the simple harmonic motion that exists after the block splits?
A5.08×10−2m,4.24HzB3.59×10−2m,4.24HzC2.54×10−2m,3.00HzD3.59×10−2m,6.00Hz
(a) The right block collides with left block and sticks to it. Find amplitude of the resulting SHM.

(b) The block starts from left wall and moves with constant speed v. All collisions are elastic. Find time period of periodic motion.

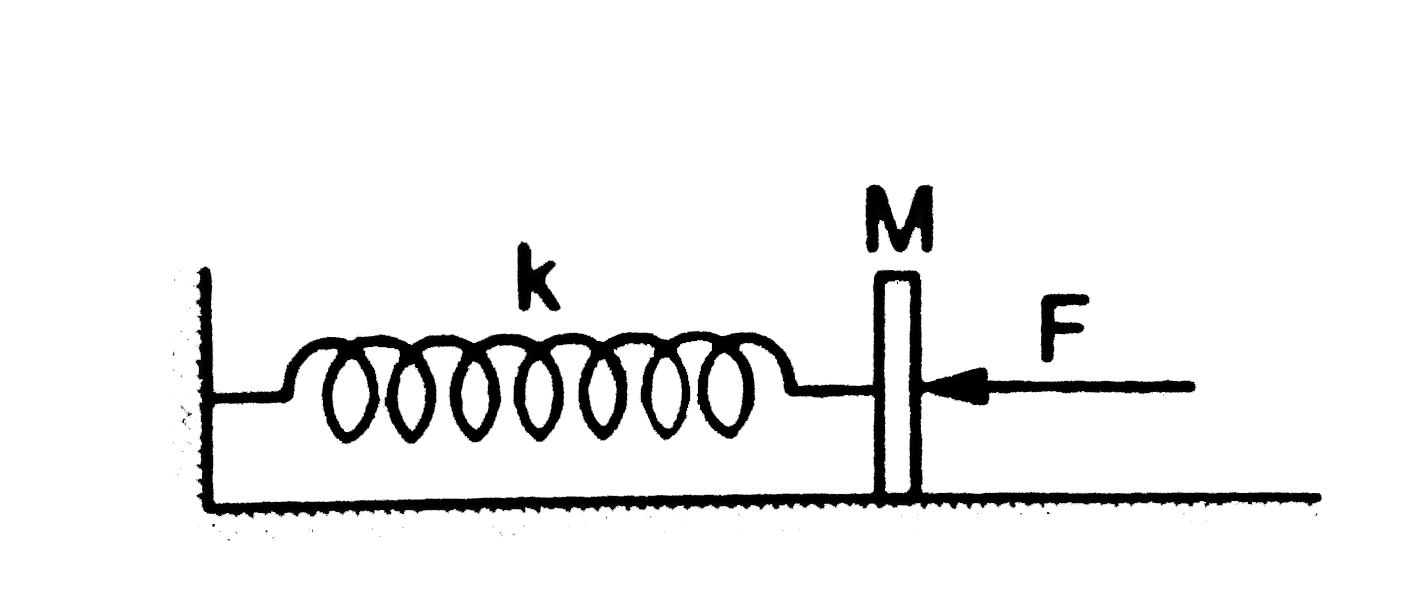
View SolutionIn figure, k=100N/m,M=1kg and F=10N

(a) Find the compression of the spring in the equilibrium position
(b) A sharp blow by some external agent imparts a speed of 2m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
(c) Find the time period of the resulting simple harmonic motion.
(d) Find the amplitude.
(e) Write the potential energy of the spring when the block is at the left estreme.
(f) Write the potential energy of the spring when the block is at the right extreme.
The answers of (b), (e) and (f) are different. Explain why this does not violate the principle of conservation of energy ?
View SolutionIn figue k=100Nm−1M=1kgandF=10N. a. Find the compression of the spring in the equilibrium position. b. A sharp blow by some xternal agent imparts a speed of 2ms−1 to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at ths instant. c. find the time period of the resulting simple harmonic motion. d. Find the ampitude. e. Write the potential energy of the spring when the block is at the left extreme. f. Write teh potential energy of the spring when teh block is at the right extreme.
The anwer of b, e, and f are different. Explain why this does not violate the principle of conservation of energy.
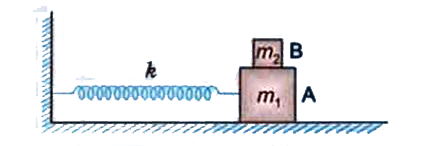
View SolutionA block A of mass m1 is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass m2 is placed on block A. The coefficient of static friction between the blocks is μ. The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?
View SolutionIn the figure shown, the block A of mass m collides with the identical block B and after collision they stick together. Calculate the amplitude of resulatant vibration.
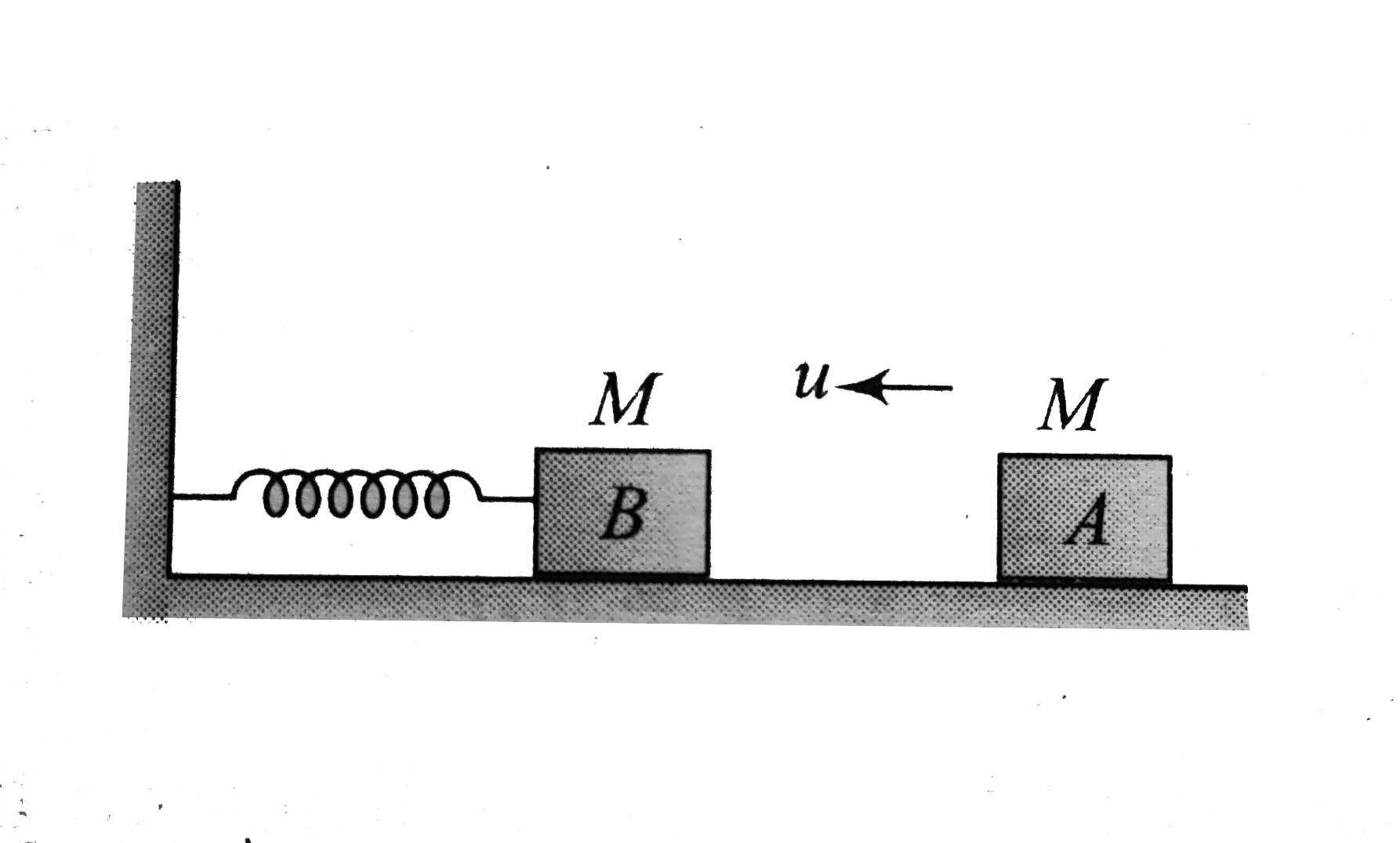
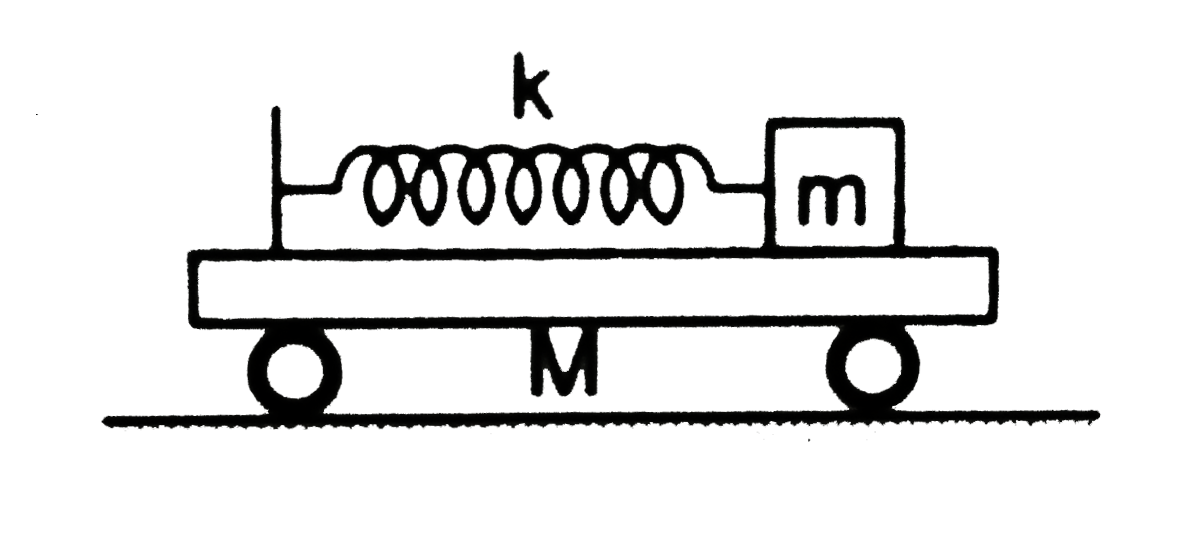
View SolutionAll the surfaces shown in figure are frictionless. The mass of the car is M, that of the block is mk and the spring has spring constant. Initialy the car and the block are at rest and the spring is stretched through a length x0 when the system is released. a. Find the amplitude of the simple harmonic motion of the blocks and of the car as seen from the road. b. Find the time periods of the two simple harmonic motions.
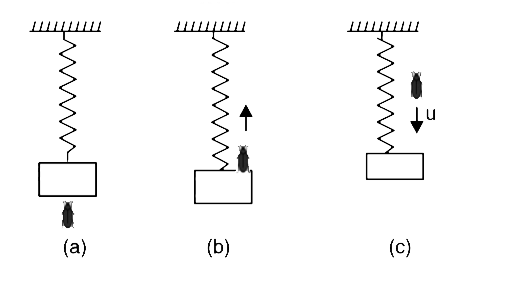
View SolutionA block of mass M is tied to a spring of force constant K and the system is suspended vertically. Consider three situations shown in fig. (a), (b) and (c).
(a) In fig. (a), an insect of mass M is clinging to the block and the system is in equilibrium. The insect leaves the block and falls. Find the amplitude of resulting oscillations.
(b) In fig. (b), an insect of mass M is resting on the top of the block and the system is in equilibrium. The insect suddenly jumps up with a speed u=g√MK and the block starts oscillating. Find amplitude of oscillation assuming that the insect never falls back on the block
(c) In fig. (c), an insect of mass M falls on the block this in equilibrium. The insect hits the block with velocity u=g√MK while moving downwards sticks to the block. Find the amplitude of oscillation.
View Solution
