A block of mass M is tied to a spring of force constant K and the system is suspended vertically. Consider three situations shown in fig. (a), (b) and (c).
(a) In fig. (a), an insect of mass M is clinging to the block and the system is in equilibrium. The insect leaves the block and falls. Find the amplitude of resulting oscillations.
(b) In fig. (b), an insect of mass M is resting on the top of the block and the system is in equilibrium. The insect suddenly jumps up with a speed u=g√MK and the block starts oscillating. Find amplitude of oscillation assuming that the insect never falls back on the block
(c) In fig. (c), an insect of mass M falls on the block this in equilibrium. The insect hits the block with velocity u=g√MK while moving downwards sticks to the block. Find the amplitude of oscillation.
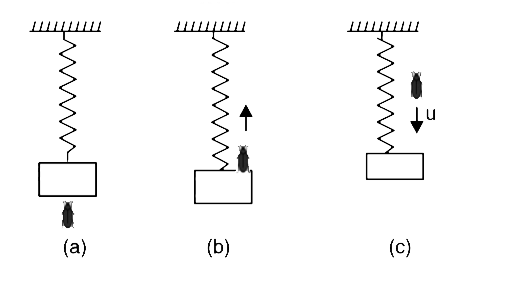
The correct Answer is:(a) MgK
(b) √2MgK
(c) √62MgK
Step by step video, text & image solution for A block of mass M is tied to a spring of force constant K and the system is suspended vertically. Consider three situations shown in fig. (a), (b) and (c). (a) In fig. (a), an insect of mass M is clinging to the block and the system is in equilibrium. The insect leaves the block and falls. Find the amplitude of resulting oscillations. (b) In fig. (b), an insect of mass M is resting on the top of the block and the system is in equilibrium. The insect suddenly jumps up with a speed u=gsqrt((M)/(K)) and the block starts oscillating. Find amplitude of oscillation assuming that the insect never falls back on the block (c) In fig. (c), an insect of mass M falls on the block this in equilibrium. The insect hits the block with velocity u=gsqrt((M)/(K)) while moving downwards sticks to the block. Find the amplitude of oscillation. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
An ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy

View SolutionLet →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .
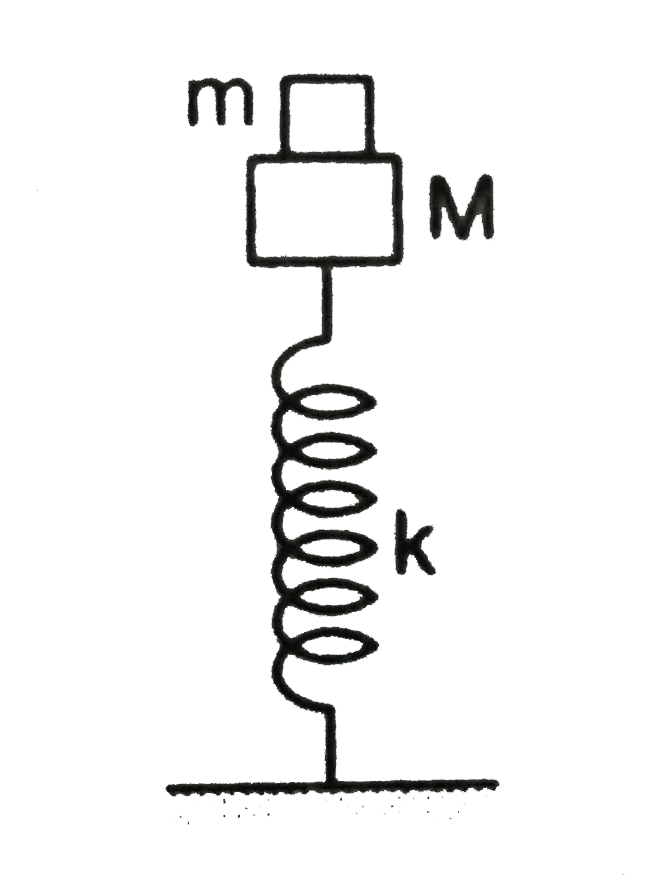
View SolutionA small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
View SolutionThree blocks A,B, and C are suspended as shown in fig. Mass of each of blocks A and B is m. If the system is in equilibrium, and mass of C is M then

View SolutionA mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring. The extension produced in the spring is given by
View SolutionA block of mass m is suspended from a spring and executes vertical SHM of time period T as shown in Fig. The amplitude of the SHM is A and spring is never in compressed state during the oscillation. The magnitude of minimum force exerted by spring on the block is
View SolutionA block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
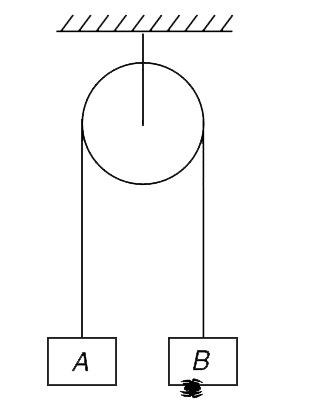
View SolutionIn the arrangement shown in the figure the system is in equilibrium. Mass of the block A is M and that of the insect clinging to block B is m. Pulley and string are light. The insect loses contact with the block B and begins to fall. After how much time the insect and the block B will have a separation L between them.
View SolutionThree blocks A,B and C are suspended as shown in the figure. Mass of each block A and C is m. if the system is in equilibrium and mass of B is M, then
View SolutionFig. 7. 187 (a) shows a system of two blocks of masses m and M(>m) placed on a surface , there is no friction between the blocks and the surface . A force F is applied to the system as shown resulting in the motion of the system .

Fig. 7.187 (b) also shows a system of blocks of masses m and M . Masses m and M have , respectively , the same values as in Fig . 7.187 (a) . There is no friction between the lower block and the surface on which the system is placed but friction is present at the constant of the two blocks . A force F, having the same value as in Fig. 7.187 (a) , is applied to the lower block resulting in the motion of the system such that both blocks move together with a common acceleration . Match Column-I and II.

View SolutionComparing the L-C oscillations with the oscillations of a spring-block system (force constant of spring=k and mass of block=m), the physical quantity mk is similar to
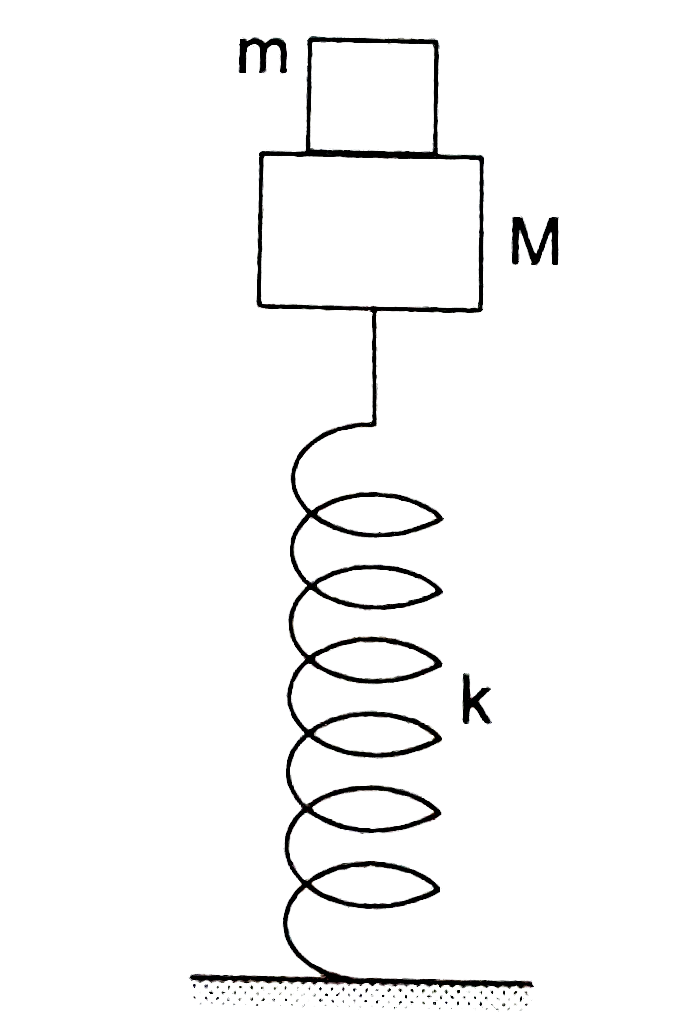
View Solutionएक स्प्रिंग को ऊर्ध्वाधर स्थिति में एक फर्श पर जड़कर रखा गया है (चित्र 21.E1) तथा इसपर M द्रव्यमान का एक ब्लॉक जड़ा हुआ है। इस ब्लॉक पर द्रव्यमान का एक दूसरा ब्लॉक रखा हुआ है। स्प्रिग के स्प्रिंग-नियताक k है। यह निकाय ऊर्ध्वाधर दोलन करता है। (a) जब ब्लॉक अपनी साम्यावस्था से x दूरी ऊपर है उस समय ऊपर बाले ब्लॉक पर परिणामी बल निकालें। (b) इस स्थिति में ऊपर वाले ब्लॉक पर नीचे बाले ब्लॉक द्वारा लगाया गया लबवत बल निकाले। इस लबवत बल का परिमाण किस स्थिति में न्यूनतम हगा? (c) दानो ब्लाकों को साथ-साथ दोलन करते रहने के लिए अधिकतम आयाम कितना हो सकता है
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
View SolutionAN oscillating block-spring system has a mechanical energy of 2.00J, an amplitude of 10.0cm, and a maximum speed of 0.800 m/s. Find (a) the spring constant, (b) the mass of the block and (c ) the frequency of oscillation.
View SolutionThree blocks A,B and C are suspended as shown in the figure. Mass of each block A and C is m. if the system is in equilibrium and mass of B is M, then

View Solution
