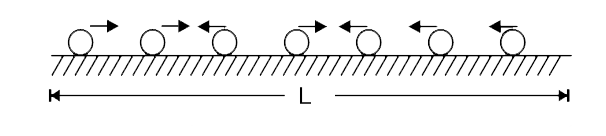
There are 40 identical balls travelling along a straight line on a smooth horizontal table. All balls have equal speed v and each one is travelling to right or left. All collisions between the balls is head on elastic. At some point in time all balls will have fallen off the table. The time at which this happens will definitely depend on initial positions of the balls. Over all possible initial positions of the balls, what is the longest amount of time that you would need to wait to ensure that the table has no more balls? Assume that length of the table is L.
The correct Answer is:Lv
Step by step video, text & image solution for There are 40 identical balls travelling along a straight line on a smooth horizontal table. All balls have equal speed v and each one is travelling to right or left. All collisions between the balls is head on elastic. At some point in time all balls will have fallen off the table. The time at which this happens will definitely depend on initial positions of the balls. Over all possible initial positions of the balls, what is the longest amount of time that you would need to wait to ensure that the table has no more balls? Assume that length of the table is L. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
An ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy

View SolutionLet →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .
View SolutionThree identical balls, ball I, ball II and ball III are placed on a smooth floor on a straight line at the separation of 10m between balls as shown in figure. Initially balls are stationary. But I is given velocity of 10m/s towards ball II, collision between balls I and II is inelastic with coefficient of restitution 0.5 but collision between balls II and III is perfectly elastic. What is the time interval between two consecutive collisions between ball I and II?

View SolutionFive balls are placed one after the other along a straight line as shown in the figure. Initially, all the balls are at rest. Then the second ball has been projected with speed v_(0) towards the third ball. Mark the correct statements, (Assume all collisions to be head-on and elastic.)
View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionTwo balls marked 1 and 2 of the same mass m and a third ball marked 3 of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball 1 moves with a velocity v1 towards ball 2. All collisions are assumed to be elastic. If M<m, the number of collisions between the balls will be.

View SolutionA smooth ball of mass M and radius R is lying on a smooth horizontal table. A smaller ball of radius r and mass m travelling horizontally on the table with velocity u hits the larger ball. Collision is elastic. During the interaction of the balls the larger ball does not lose contact with the table at any instant

(i) Calculate the velocity of the balls after collision.
(ii) Calculate the maximum possible interaction force between the balls during collision.
View SolutionTwo billiard balls undergo a head-on collision. Ball 1 is twice as heavy as ball 2. Initially, ball 1 moves with a speed v towards ball 2 which is at rest. Immediately after the collision, ball 1 travels at a speed of v/3 in the same direction. What type of collision has occured?
View SolutionTwo billiard balls undergo a head-on collision. Ball 1 is twice as heavy as ball 2. Initially, ball 1 moves with a speed v towards ball 2 which is at rest. Immediately after the collision, ball 1 travels at a speed of v/3 in the same direction. What type of collision has occured ?
View SolutionTwo billiard balls undergo a head-on collision. Ball 1 is twice as heavy as ball 2. Initially, ball 1 moves with a speed v towards ball 2 which is at rest. Immediately after the collision, ball 1 travels at a speed of v/3 in the same direction. What type of collision has occured ?
View SolutionTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is

View SolutionThree identical spherical balls A, B and C are placed on a table as shown in the figure along a straight line. B and Care at rest initially.

The ball A hits B head on with a speed of 10ms−1. Then after all collisions (assumed to be elastic) A and B are brought to rest and C takes off with a velocity of
View SolutionThree identical balls, ball I, ball II and ball III are placed on a smooth floor on a straight line at the separation of 10m between balls as shown in figure. Initially balls are stationary. But I is given velocity of 10m/s towards ball II, collision between balls I and II is inelastic with coefficient of restitution 0.5 but collision between balls II and III is perfectly elastic. What is the time interval between two consecutive collisions between ball I and II?

View SolutionTwo balls marked 1 and 2 of the same mass m and a third ball marked 3 of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball 1 moves with a velocity v1 towards ball 2. All collisions are assumed to be elastic. If M<m, the number of collisions between the balls will be.

View SolutionTwo balls marked 1 and 2 of the same mass m and a third ball marked 3 of mass M are arranged over a smooth horizontal surface as shown in the figure. Ball 1 moves with a velocity v_(1) towards ball 2. All collisions are assumed to be elastic. If Mltm , the number of collisions between the balls will be.
View Solution
