There particles A, B and C have masses m, 2m and m respectively. They lie on a smooth horizontal table connected by light inextensible strings AB and BC. The string are taut and <ABC=120∘. An impulse is applied to particle A along BA so that it acquires a velocity u. Find the initial speeds of B and C.

The correct Answer is:vB=2√3111u,vc=4u11
Step by step video, text & image solution for There particles A, B and C have masses m, 2m and m respectively. They lie on a smooth horizontal table connected by light inextensible strings AB and BC. The string are taut and lt ABC = 120^(@). An impulse is applied to particle A along BA so that it acquires a velocity u. Find the initial speeds of B and C. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
An ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy
View SolutionLet →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .
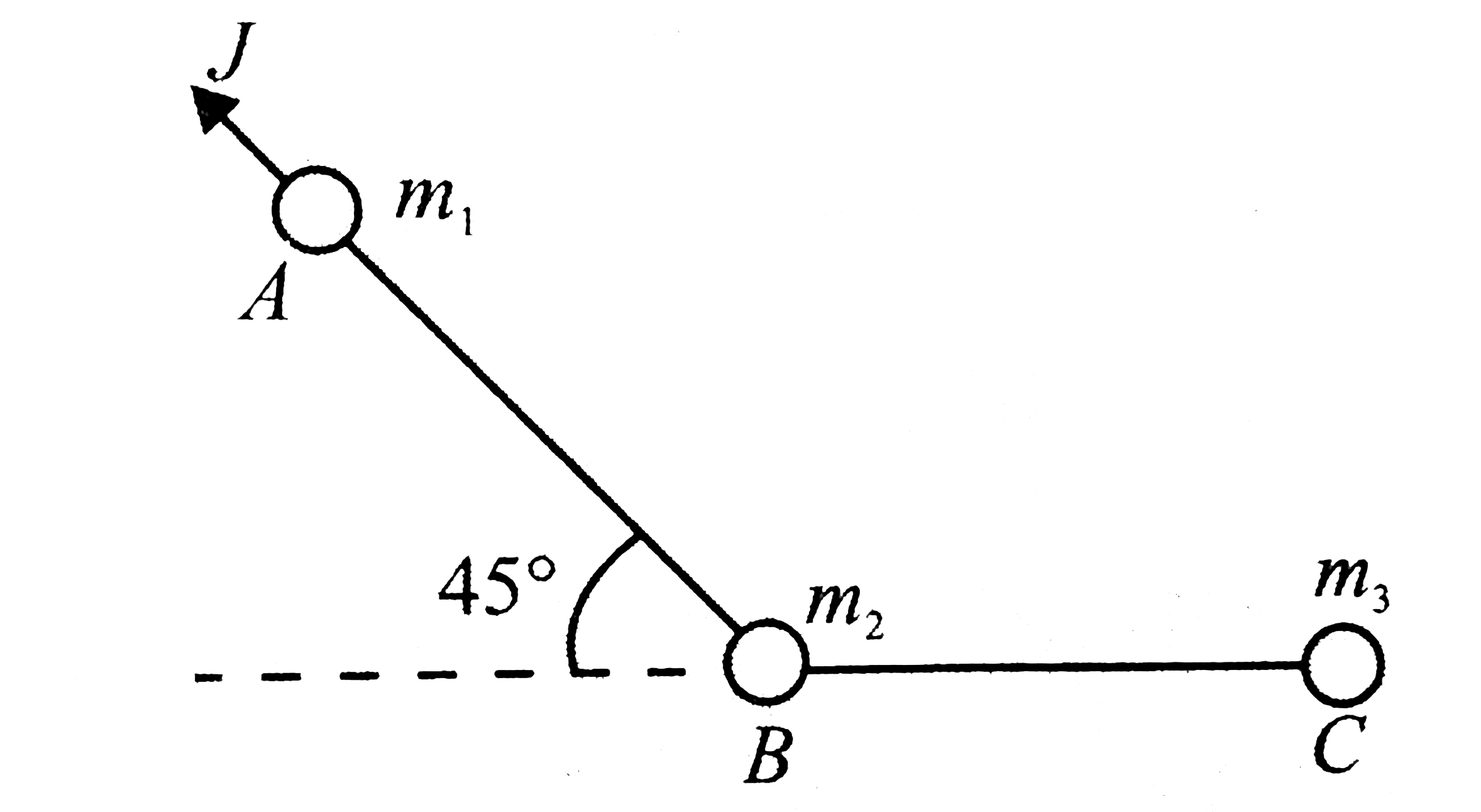
View SolutionThree particles A,B and C of respective masses m1,m2 and m3 lie on a smooth horizontal surface, and an fastened to two light inextensible strings as shown in Fig. The particle A is imparted an impulse J along −−→BA . Find the initial speed of each particle.
View SolutionThree identical particles A, B and C of mass m lie on a smooth horizontal table. Light inextensible strings which are just taut connect AB and BC and angleABC is 135° . An impulse J is imparted to the particle C in the direction BC. Mass of each particle is m. Choose the correct options.
View SolutionA particle of mass 2m is connected by an inextensible string of length 1.2m to a ring of mass m which is free to slide on a horizontal smooth rod. Initially the ring and the particle are at the same level with the string taut. Both are then released simultaneously. The distance in meter moved by the ring when the string becomes veritcal is :-
View SolutionTwo particles, each of mass m, are connected by a light inextensible string of lenthe 2l . Initially they lie on a smooth horizontal table at points A and B distant l apart. The particle at A is projected across the table with velocity u. Find the speed with which the second particle begins to move if the direction of u is :- (i) along BA. (ii) at an angle of 120^(@) with AB (iii) perpendicular to AB. In each case calculate (in teerms of m and u) the impulsive tension in the string.
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionTwo particles, each of m, are connected by a light inextensible string of length 2l. Initially they lie on a smooth horizontal table at points A and B distant l apart. The particle at A is projected across the table with velocity u. Find the speed with which the second particle begins to move if the direction of u is , (a) along BA, (b) at an angle of 120∘ with AB, (c) perpendicular to AB. In each case calculate (in terms of m and u) the impulse of tension in the string.
View SolutionTwo particle of equal mass m at A and B are connected by a rigid light rod AB lying on a smooth horizontal table. An impulse J is applied at A in the plane of the table and perpendicular at AB . The velocity of particle at A is
View SolutionTwo particle, each of mass m, are connected by a light inextensible string of length 2l. Initially they lie on a smooth horizontal table at points A ad B distant l apart the particle at A is projectd across the table with velocity u. find th speed with which the second particle begins to move if the direction. of u is : (a). along BA (b). at an angle of 120^(@) with AB (c) perpendicular to AB In each case also calculate (in terms of ma nd u) the impulsive tension in the string.
View SolutionTwo particles of equal mass m at A and B are connected by a rigid light rod AB lying on a smooth horizontal table. An impulse J is applied at A in the plane of the table and perpendicular at AB. Then the velocity of particle at A is :
View SolutionA = B = C = 4 kg. The table is smooth, the string is light and inextensible. The tension in the string connecting B and C is
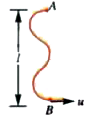
View SolutionA string AB of length 21 is fixed at A to a point on a smooth horizontal table. A particle - of mass m attached to B is initially at a distance I from A as shown in figure. The particle is projected horizontally with speed u at right angles to AB. Find the impulsive tension in the string when it becomes taut and the velocity of the particle immediately afterwards.
View SolutionThree particles A,B and C of respective masses m1,m2 and m3 lie on a smooth horizontal surface, and an fastened to two light inextensible strings as shown in Fig. The particle A is imparted an impulse J along −−→BA . Find the initial speed of each particle.

View SolutionThree identical particles A, B and C of mass m lie on a smooth horizontal table. Light inextensible strings which are just taut connect AB and BC and ∠ABC is 135° . An impulse J is imparted to the particle C in the direction BC. Mass of each particle is m. Choose the correct options.

View Solution
