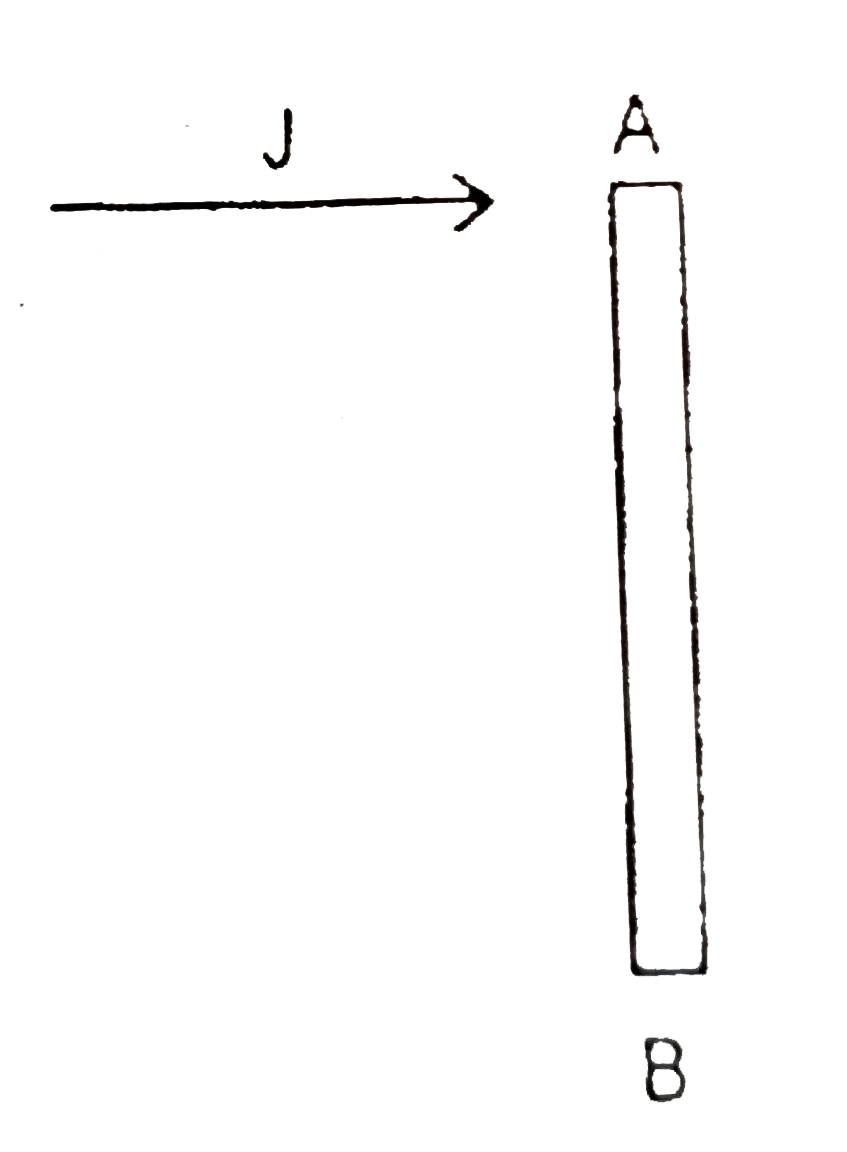
Two particles of equal mass m at A and B are connected by a rigid light rod AB lying on a smooth horizontal table. An impulse J is applied at A in the plane of the table and perpendicular at AB. Then the velocity of particle at A is :
J2m
Jm
2Jm
zero
The correct Answer is:B
To solve the problem, we need to analyze the situation involving two particles connected by a rigid rod and the effect of the applied impulse. Let's break down the solution step by step.
1. Understanding the System:
- We have two particles of equal mass m located at points A and B.
- They are connected by a rigid light rod AB on a smooth horizontal table.
- An impulse J is applied at point A perpendicular to the rod AB.
2. Defining the Impulse:
- The impulse J causes a change in momentum for the particle at A.
- Since the impulse is applied perpendicular to the rod, it will also create an angular motion about the center of mass of the system.
3. Calculating Angular Impulse:
- The angular impulse τ about the center of mass C can be calculated as:
τ=J⋅d
where d is the distance from the center of mass to point A. Since the masses are equal and the rod is uniform, the center of mass is at the midpoint, so d=l2.
4. Relating Angular Impulse to Angular Momentum:
- The change in angular momentum ΔL is equal to the angular impulse:
ΔL=J⋅l2
5. Moment of Inertia Calculation:
- The moment of inertia I of the system about the center of mass is given by:
I=m(l2)2+m(l2)2=2m(l2)2=ml22
6. Using the Relation of Angular Momentum:
- The angular momentum L can also be expressed as:
L=Iω
- Setting the angular impulse equal to the change in angular momentum gives:
J⋅l2=ml22ω
7. Solving for Angular Velocity ω:
- Rearranging the equation to solve for ω:
ω=Jml
8. Finding the Velocity of Particle at A:
- The linear velocity vA of particle A can be related to the angular velocity ω by:
vA=l2ω
- Substituting for ω:
vA=l2⋅Jml=J2m
9. Final Result:
- Therefore, the velocity of particle at A is:
vA=J2m
- We have two particles of equal mass m located at points A and B.
- They are connected by a rigid light rod AB on a smooth horizontal table.
- An impulse J is applied at point A perpendicular to the rod AB.
- The impulse J causes a change in momentum for the particle at A.
- Since the impulse is applied perpendicular to the rod, it will also create an angular motion about the center of mass of the system.
- The angular impulse τ about the center of mass C can be calculated as:
τ=J⋅d
where d is the distance from the center of mass to point A. Since the masses are equal and the rod is uniform, the center of mass is at the midpoint, so d=l2.
- The change in angular momentum ΔL is equal to the angular impulse:
ΔL=J⋅l2
- The moment of inertia I of the system about the center of mass is given by:
I=m(l2)2+m(l2)2=2m(l2)2=ml22
- The angular momentum L can also be expressed as:
L=Iω
- Setting the angular impulse equal to the change in angular momentum gives:
J⋅l2=ml22ω
- Rearranging the equation to solve for ω:
ω=Jml
- The linear velocity vA of particle A can be related to the angular velocity ω by:
vA=l2ω
- Substituting for ω:
vA=l2⋅Jml=J2m
- Therefore, the velocity of particle at A is:
vA=J2m
Topper's Solved these Questions
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 2 (Level - II)
25 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 3 (Level - I)
27 Videos
- 10 ROTATIONALBOOK - MOTIONCHAPTER - 10 ROTATIONALEXERCISE - Exercise - 1
77 Videos
- ALTERNATING CURRENTBOOK - MOTIONCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - 4 (LEVEL - II)
14 Videos
Similar Questions
Two particles each of mass M are connected by a massless rod. The rod is lying on the smooth horizontal surface. If one of the particle is given an impulse MV as shown in the figure then angular velocity of the system would be:

View SolutionTwo particles A and B, each of mass m, are connected by a light rod of length L lying on a smooth horizontal surface. A particle of mass m moving with speed v0 strikes to the end of rod and sticks to A as shown . Find
(a) the velocity of the center of mass,
(b) the angular velocity about the center of mass of system (A+B+ particle) and
(c) the linear speeds of A and B immediately after collision.

View Solution
Knowledge Check
Two particle of equal mass m at A and B are connected by a rigid light rod AB lying on a smooth horizontal table. An impulse J is applied at A in the plane of the table and perpendicular at AB. The velocity of particle at A is
AJ2mBJmC2JmDzeroTwo particles connected by a rigid light rod AB, lying on a smooth horizontal table. An impulse J is applied at A in the plane of thetable and perpendicular at AB. Then the velocity of particle at A is
AJ2mBJmC2JmDzeroA rod AB of mass M and length L lies on smooth horizontal table impulse J is applied to end A as shown in the figure immediately after imparting the impulse :
 AThe radius of curvature of trajectory of A as seen from the ground is 89L.BThe radius of curvature of trajectory of B as seen from the ground is 29L.CThe instantaneous axis of rotation is at a distance of L/6 from the mid point of the rod.Dthe mid point of the rod will move along a straight line.
AThe radius of curvature of trajectory of A as seen from the ground is 89L.BThe radius of curvature of trajectory of B as seen from the ground is 29L.CThe instantaneous axis of rotation is at a distance of L/6 from the mid point of the rod.Dthe mid point of the rod will move along a straight line.
Two particles (A and B) of masses m and 2m are joined by a light rigid rod of length L. The system lies on a smooth horizontal table. The particle (A) of mass m is given a sharp impulse so that it acquires a velocity u perpendicular to the rod. Calculate maximum speed of particle B during subsequent motion. By what angle θ will the rod rotate by the time the speed of particle B become maximum for the first time ?

View SolutionTwo particles A and B of equal mass m are attached by a string of length 2l and initially placed over a smooth horizontal table in the positoin shown in fig. particle B is projected across the table with speed u perpendicular to AB as shown in the figure. find the velocities of each particle after the string becomes taut and the magnitude of the impulse tension.
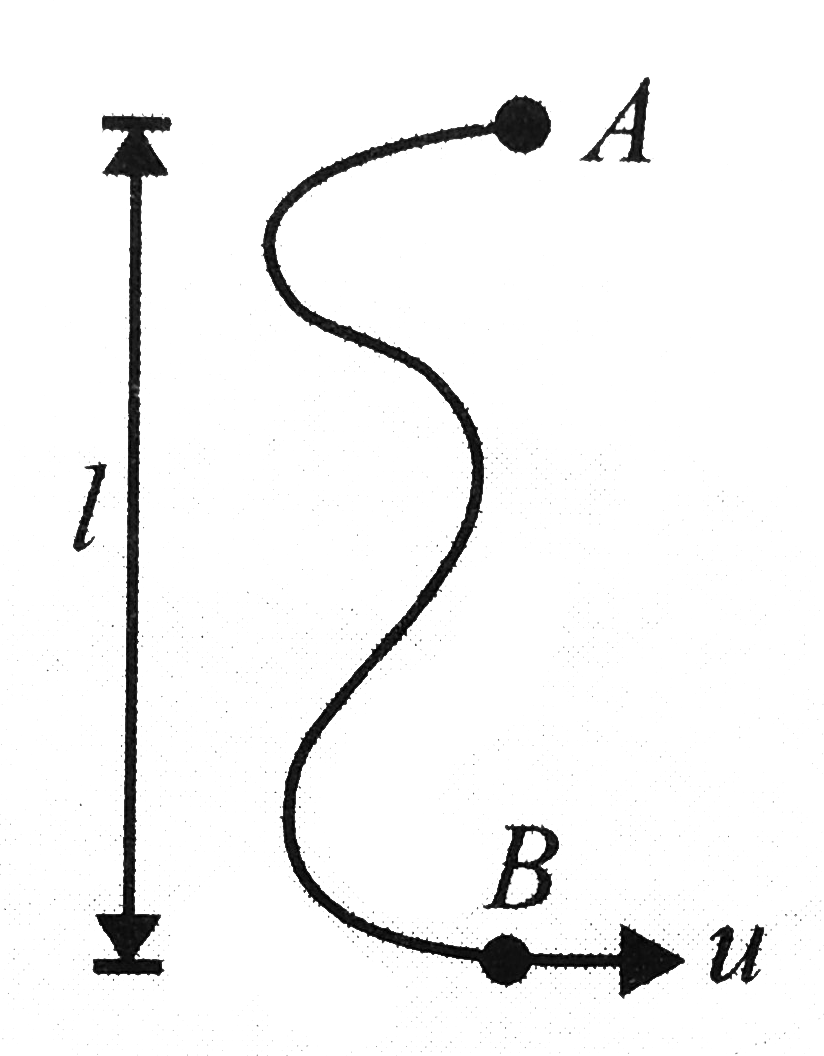
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionTwo particles, each of mass m, are connected by a light inextensible string of lenthe 2l. Initially they lie on a smooth horizontal table at points A and B distant l apart. The particle at A is projected across the table with velocity u. Find the speed with which the second particle begins to move if the direction of u is :-
(i) along BA.
(ii) at an angle of 120∘ with AB
(iii) perpendicular to AB. In each case calculate (in teerms of m and u) the impulsive tension in the string.
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
View Solution
