A uniform rod of mass and length is at rest on a smooth horizontal surface. An impulse is applied to the end , perpendicular to the rod in the horizontal direction. Speed of particlem at a distance from the centre towards of the rod after time is.
The correct Answer is:D
To find the speed of the particle P at a distance l6 from the center towards A of the rod after time t=πml12J, we can follow these steps:
Step 1: Determine the Linear Velocity of the Center of Mass (VCM)
The impulse J applied to the rod will impart a linear momentum to the center of mass. By the conservation of linear momentum, we have:
J=m⋅VCM
From this, we can solve for VCM:
VCM=Jm
Step 2: Determine the Angular Velocity (ω)
The impulse also causes the rod to rotate about its center of mass. The torque τ due to the impulse about the center of mass is given by:
τ=J⋅l2
Using the relation for torque and angular momentum, we have:
τ=I⋅ω
where I is the moment of inertia of the rod about its center, given by:
I=112ml2
Setting the two expressions for torque equal gives:
J⋅l2=112ml2⋅ω
Solving for ω:
ω=6Jml
Step 3: Determine the Angle of Rotation (θ)
The angle of rotation θ after time t can be found using the formula:
θ=ω⋅t
Substituting t=πml12J:
θ=(6Jml)⋅(πml12J)=π2
Step 4: Determine the Velocity of Particle P
The particle P is located at a distance l6 from the center of mass. It has two components of velocity:
1. The translational velocity VCM in the direction of motion.
2. The tangential velocity due to rotation, which is given by vtangential=ω⋅r, where r=l6.
Calculating the tangential velocity:
vtangential=ω⋅l6=(6Jml)⋅l6=Jm
Step 5: Total Velocity of Particle P
The total velocity VP of particle P is the vector sum of the translational and tangential velocities:
VP=√V2CM+v2tangential
Substituting the values we found:
VP=√(Jm)2+(Jm)2=√2(Jm)2=Jm√2
Final Answer
The speed of particle P at a distance l6 from the center towards A of the rod after time t=πml12J is:
VP=Jm√2
The impulse J applied to the rod will impart a linear momentum to the center of mass. By the conservation of linear momentum, we have:
The impulse also causes the rod to rotate about its center of mass. The torque τ due to the impulse about the center of mass is given by:
The angle of rotation θ after time t can be found using the formula:
The particle P is located at a distance l6 from the center of mass. It has two components of velocity:
2. The tangential velocity due to rotation, which is given by vtangential=ω⋅r, where r=l6.
The total velocity VP of particle P is the vector sum of the translational and tangential velocities:
The speed of particle P at a distance l6 from the center towards A of the rod after time t=πml12J is:
Similar Questions
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:
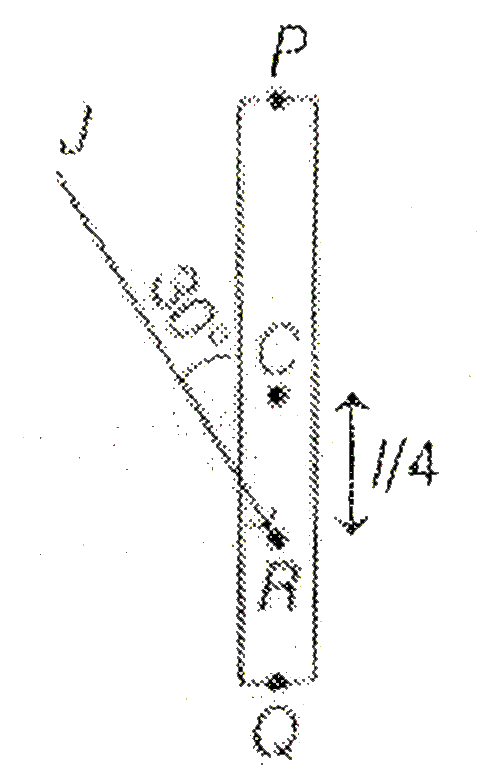
View Solution
Knowledge Check
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
A2JmBJ√2mCJmD√2JmA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse p is applied to the end B. The time taken by the rod to turn through a right angle is
A(2πmlpB(2π)(pmlCπml12pDπpmlA uniform rod AB of mass m and length l at rest on a smooth horizontal surface. An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 A2πmlPBπml3PCπml12PD2πml3P
A2πmlPBπml3PCπml12PD2πml3P
A uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.

Distance travelled by the centre of the rod, while rod rotates by 90∘
View SolutionA uniform rod of mass m and length l is at rest on smooth horizontal surface. An impulse P is applied to end B as shown.
The point about which rod rotates just after impulse being applied is located at
View SolutionA rod AB of mass M and length L lies on smooth horizontal table impulse J is applied to end A as shown in the figure immediately after imparting the impulse :
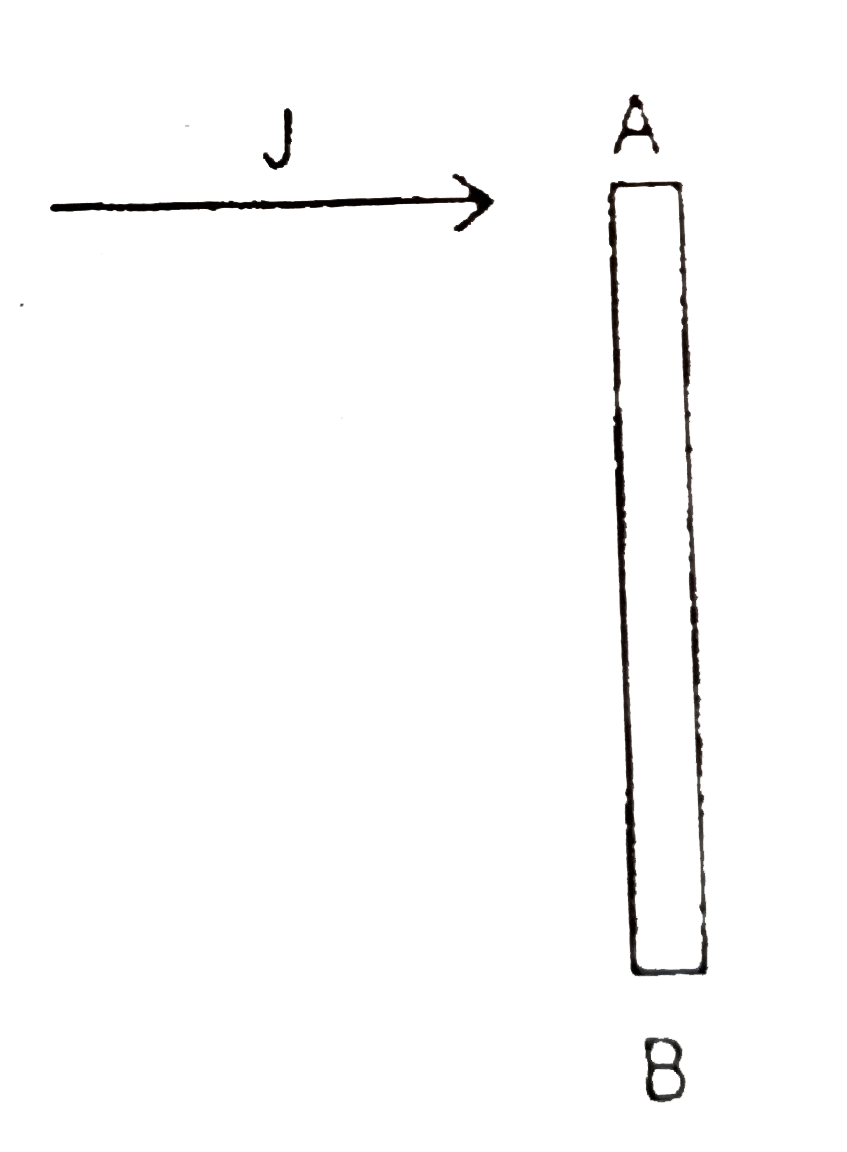
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View Solution
