A ball is projected downward from the top of a cliff of height h with an initial speed v.Another ball is simultaneously projected vertically up from the bottommost of the cliff with the same speed.When do they meet?
To solve the problem of when the two balls meet, we can follow these steps:
Step 1: Define the Variables
Let:
- h = height of the cliff
- v = initial speed of both balls
- t = time after projection when the balls meet
- g = acceleration due to gravity (approximately 9.81m/s2)
Step 2: Write the Equation for the Downward Projected Ball
The first ball is projected downward from the top of the cliff. The distance it travels after time t can be expressed using the second equation of motion:
S1=vt+12gt2
Here, S1 is the distance traveled by the first ball.
Step 3: Write the Equation for the Upward Projected Ball
The second ball is projected upward from the bottom of the cliff. The distance it travels after time t is given by:
S2=vt−12gt2
Here, S2 is the distance traveled by the second ball.
Step 4: Set Up the Equation for Meeting Point
Since the total distance covered by both balls when they meet must equal the height of the cliff, we can write:
S1+S2=h
Substituting the expressions for S1 and S2:
(vt+12gt2)+(vt−12gt2)=h
This simplifies to:
2vt=h
Step 5: Solve for Time t
Now, we can solve for t:
t=h2v
Final Result
The two balls will meet after a time t=h2v.
---
Let:
- h = height of the cliff
- v = initial speed of both balls
- t = time after projection when the balls meet
- g = acceleration due to gravity (approximately 9.81m/s2)
The first ball is projected downward from the top of the cliff. The distance it travels after time t can be expressed using the second equation of motion:
S1=vt+12gt2
Here, S1 is the distance traveled by the first ball.
The second ball is projected upward from the bottom of the cliff. The distance it travels after time t is given by:
S2=vt−12gt2
Here, S2 is the distance traveled by the second ball.
Since the total distance covered by both balls when they meet must equal the height of the cliff, we can write:
S1+S2=h
Substituting the expressions for S1 and S2:
(vt+12gt2)+(vt−12gt2)=h
This simplifies to:
2vt=h
Now, we can solve for t:
t=h2v
The two balls will meet after a time t=h2v.
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (objective)
14 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Comprehension (I)
3 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Video
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
A ball is prouected vertical up from the top of a cliff of height h with a speed v1 Another ball is projected vertically up with a speed v2 from the bottom of the cliff, after a time t0 from the instantof projection of the first ball, When will the balls meet?.
View SolutionTwo bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10 and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.
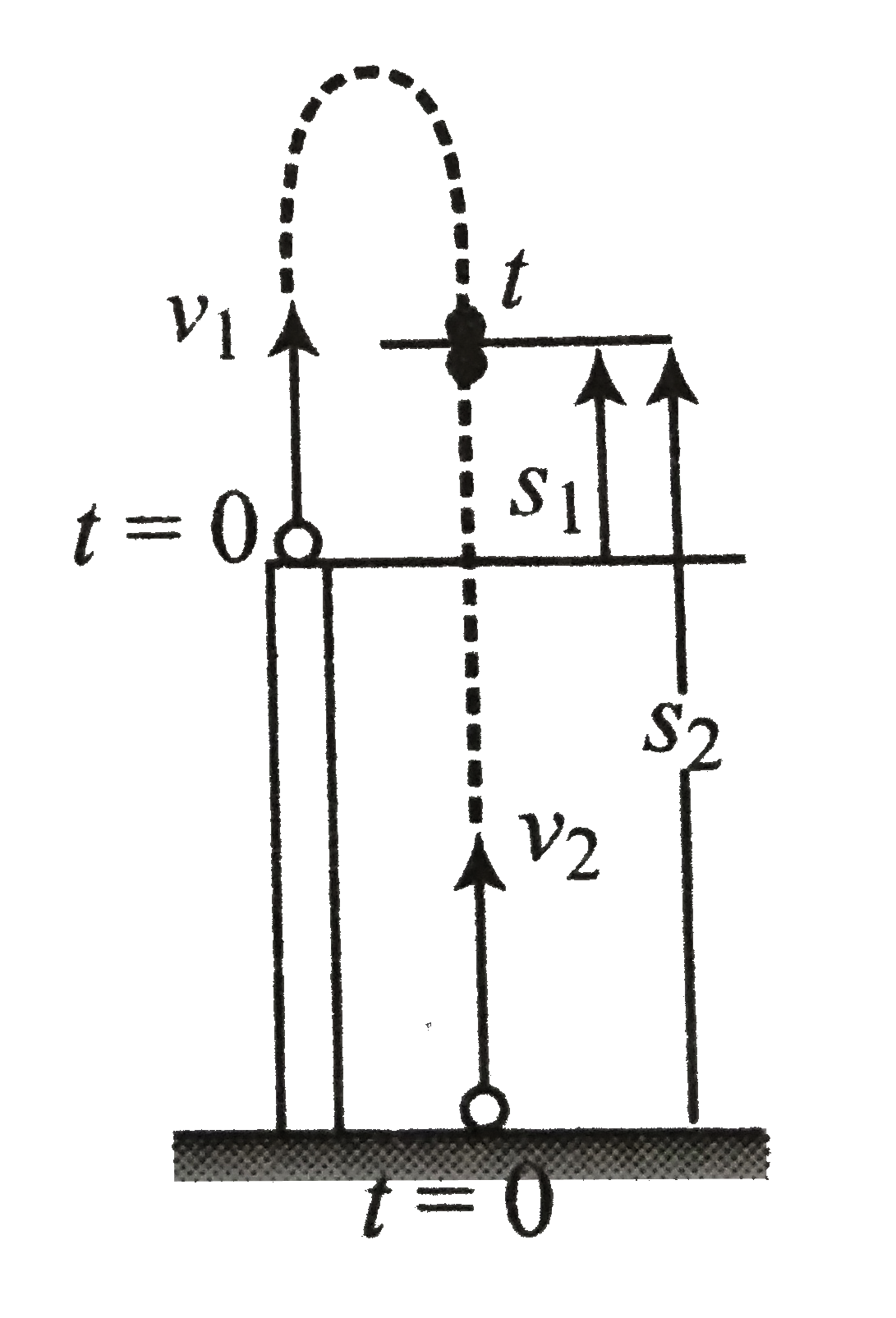
View Solution
Knowledge Check
A ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
A1.6 sB5 sC8 sD10 sA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
Avg[1+√1+2ghv2]Bvg[1+√1−2ghv2]Cvg(1+2ghv2)1/2Dvg(1−2ghv2)1/2From the top of a tower of height 200 m, a ball A is projected up with speed 10ms−1 and 2 s later, another ball B is projected vertically down with the same speed. Then
ABoth A and B will reach the ground simultaneouslyBBall A with hit the ground 2 s later than B hitting the groundCBoth the balls will hit the ground with the same velocityDBoth will rebound to the same height from the ground, if both have same coefficient of restitution.
A stone is released from the top of a cliff .Another particles is simultaneously projected v=10msec from the bottom of the cliff if they meet after 2 second find the height of the cliff.
View SolutionTwo paarticles 1 and 2 are projected simultaneusly with velocities v1 and v2, respectively. Particle 1 is projectected vertically up from the top of a cliff of heitht h and particle 2 is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
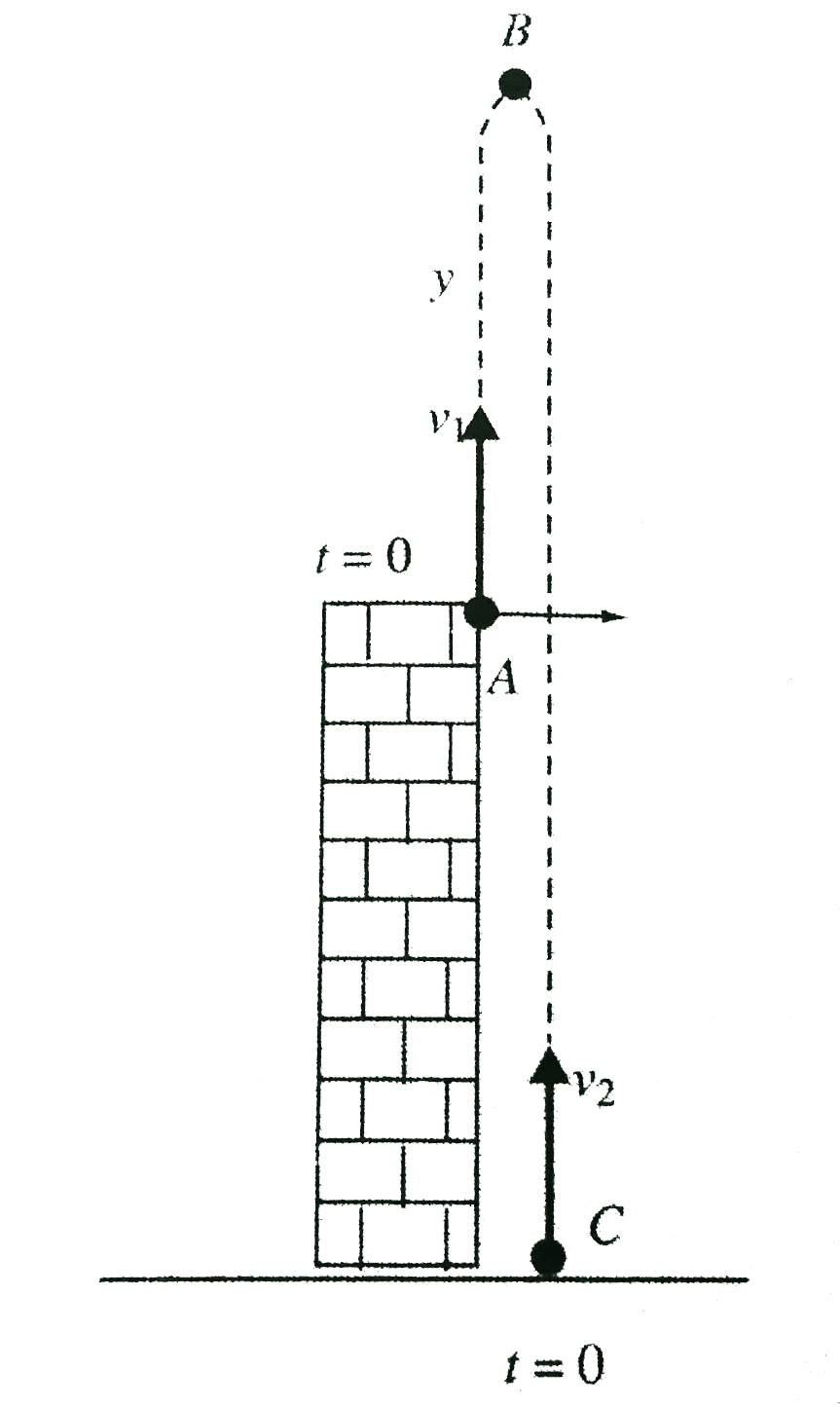 .
.
View Solution
A stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity 100m/s. Find when and where the two stones meet?
View SolutionFrom the top of a tower of height 200m, a ball A is projected up with 10ms−1. And 2s later another ball B is projected verticall down with the same speed. Then .
View SolutionA ball is projected from the ground at a speed of 10ms−1 making an angle of 30∘ with the horizontal. Another ball is simultaneously released from a point on the vertical line along the maximum height of the projectile. The initial height of the second ball is
(Take g=10ms−2)
View Solution
