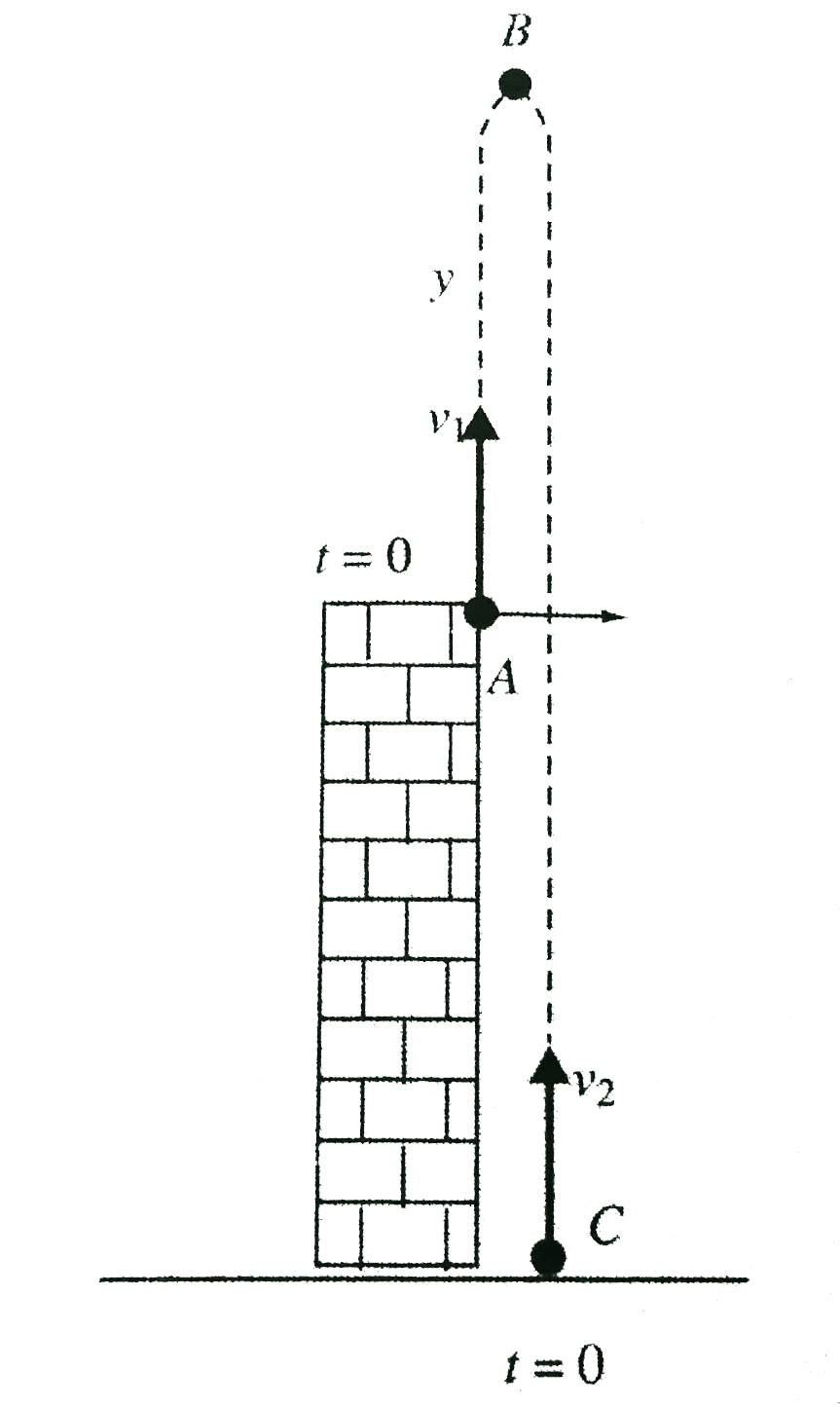
Two paarticles $1$ and $2$ are projected simultaneusly with velocities $v_{1}$ and $v_{2}$ , respectively. Particle $1$ is projectected vertically up from the top of a cliff of heitht $h$ and particle $2$ is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
.

Video Solution

Text Solution

Verified by Experts

The point of collision above the top of the cliff. Let the particle meet after time $t$ .
For first particle, $s = s_{1}, v_{0} = v_{1}, a = - g$ .
Then, $s_{1} = v_{1} t - \frac{1}{2} g t^{2}$ (ii)
For second particle, $s = s_{2}, v_{0} = v_{2}, a = - g$ .
Referring to.
$s_{2} - s_{1} = h$ (iii)
Substituting $s_{1}$ from (i), $s_{2}$ from (ii) in (iii), we have
$t = \frac{h}{(v_{2} - v_{1})}$
.
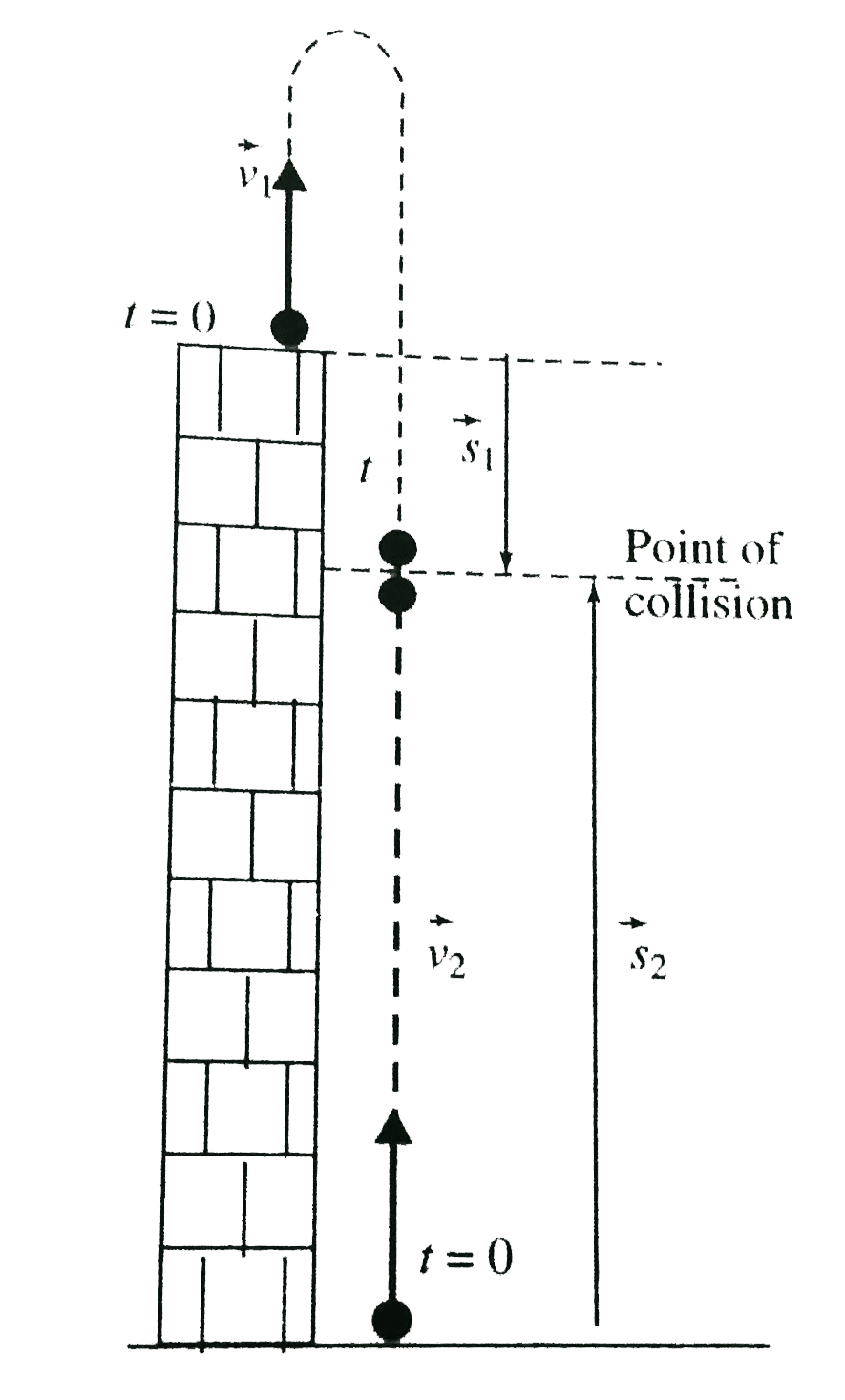
b. The point of collision of the paricle in between the top an battom of the cliff.
.
For the first particle, $s = - s_{1}, v_{0} = v_{1}$ and $a = - g$
Position-time relation for first particle,
$s_{1} = v_{1} t - \frac{1}{2} g t^{2}$
This gives $= \frac{1}{2} g t^{2} - v_{1} t$ (i)
Similarly, for the second particle, $s = 2_{2}, v_{0} = v_{2}$ , and $a = - g$ .
Then $S_{2} = v_{2} t - \frac{1}{2} g t^{2}$ (ii)
Referring to Find , $s_{1} + s_{2} = h$ , (iii)
$t = \frac{h}{(v_{2} - v_{1})}$
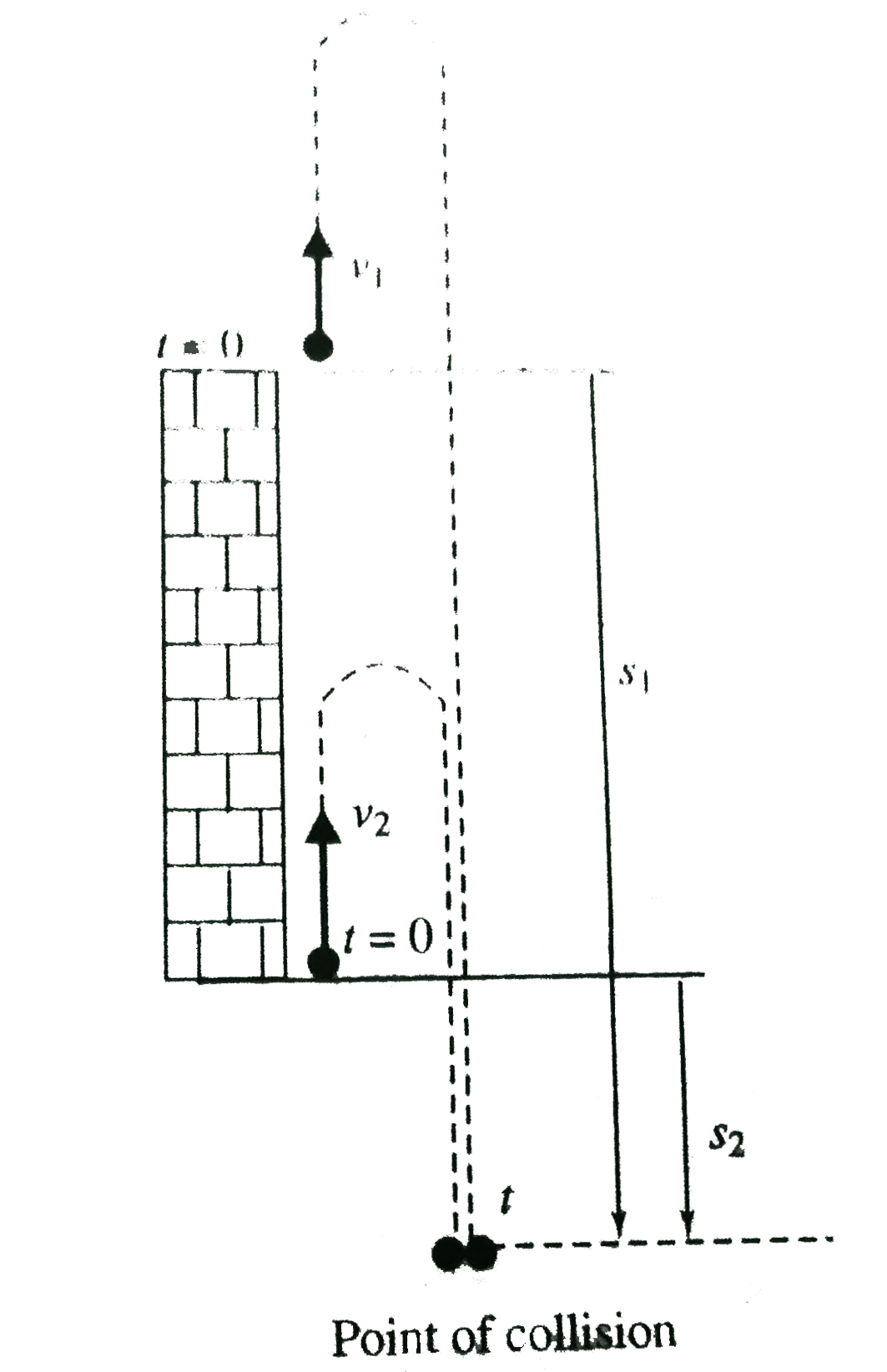
c. The point collision of the particles below the bottom of the cliff (let us assume a ditch at the base of base of the Cliff).
.
For article $1, s = - s_{1}, v_{0} = v_{1}$ , and $a = - g$ .
Position-time relation for first particl
$- s_{1} = v_{1} t - \frac{1}{2} g t^{2}$
This gives $S_{1} = \frac{1}{2} g t^{2} - v_{1} t$ (i)
Similarly, For particle (2), $= - s_{2}, v_{0} = v_{2}$ , and $a = - g$ .
We have $s_{2} = \frac{1}{2} g t^{2} - v_{2} t$ (ii)
Substituting $s_{1}$ from (i), $s_{2}$ From (ii) in (iii), we have
$t = \frac{h}{v_{2} - v_{1}}$ .

Updated on:21/07/2023

Arrange the different parts of the root vertically, from the top to the bottom.
ARegion of elongation $\to$ Root hair $\to$ Region of maturation $\to$ Region of meristematic activity $\to$ Root cap
BRegion of maturation $\to$ Root hair $\to$ Region of elongation $\to$ Region of meristematic activity $\to$ Root cap
CRegion of maturation $\to$ Region of elongation $\to$ Region of meristematic activity $\to$ Root cap $\to$ Root hair
DRoot cap $\to$ Region of meristematic activity $\to$ Region of elongation $\to$ Root hair $\to$ Region of maturation
From the top of a cliff 50m high, the angles of depression of the top and bottom of a tower are observed to be $30^{\circ}$ and $45^{\circ}$ The height of tower is
A50 m
B $50 \sqrt{3}$
C $50 (\sqrt{3} - 1)$
D $50 (1 - \frac{\sqrt{3}}{3})$ m