A stone is released from the top of a cliff .Another particles is simultaneously projected v=10msec from the bottom of the cliff if they meet after 2 second find the height of the cliff.
To find the height of the cliff from which a stone is released and where another particle is projected upwards, we can follow these steps:
1. Understand the Problem:
- A stone is released from the top of a cliff (initial velocity u1=0).
- Another particle is projected upwards from the bottom of the cliff with an initial velocity u2=10m/s.
- They meet after t=2s.
- We need to find the height H of the cliff.
2. Define the Variables:
- Let H be the height of the cliff.
- The displacement of the stone after t seconds is given by the equation of motion:
s1=u1t+12at2
- For the stone (falling down), u1=0 and a=g=10m/s2:
s1=0⋅t+12⋅10⋅t2=5t2
3. Calculate the Displacement of the Stone:
- After t=2s:
s1=5⋅(22)=5⋅4=20m
- Therefore, the stone falls 20 m downwards.
4. Calculate the Displacement of the Upward Particle:
- The displacement of the particle projected upwards is given by:
s2=u2t−12gt2
- For the upward particle, u2=10m/s and g=10m/s2:
s2=10⋅t−12⋅10⋅t2
- After t=2s:
s2=10⋅2−12⋅10⋅(22)=20−20=0m
- This means the upward particle reaches the maximum height at t=2s.
5. Relate the Heights:
- At the time they meet, the total height of the cliff H is the distance fallen by the stone plus the distance traveled by the upward particle:
H=s1+s2
- Since s2=0:
H=20+0=20m
6. Conclusion:
- The height of the cliff is H=20m.
- A stone is released from the top of a cliff (initial velocity u1=0).
- Another particle is projected upwards from the bottom of the cliff with an initial velocity u2=10m/s.
- They meet after t=2s.
- We need to find the height H of the cliff.
- Let H be the height of the cliff.
- The displacement of the stone after t seconds is given by the equation of motion:
s1=u1t+12at2
- For the stone (falling down), u1=0 and a=g=10m/s2:
s1=0⋅t+12⋅10⋅t2=5t2
- After t=2s:
s1=5⋅(22)=5⋅4=20m
- Therefore, the stone falls 20 m downwards.
- The displacement of the particle projected upwards is given by:
s2=u2t−12gt2
- For the upward particle, u2=10m/s and g=10m/s2:
s2=10⋅t−12⋅10⋅t2
- After t=2s:
s2=10⋅2−12⋅10⋅(22)=20−20=0m
- This means the upward particle reaches the maximum height at t=2s.
- At the time they meet, the total height of the cliff H is the distance fallen by the stone plus the distance traveled by the upward particle:
H=s1+s2
- Since s2=0:
H=20+0=20m
- The height of the cliff is H=20m.
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (subjective)
10 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (objective)
14 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Video
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
Two paarticles 1 and 2 are projected simultaneusly with velocities v1 and v2, respectively. Particle 1 is projectected vertically up from the top of a cliff of heitht h and particle 2 is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
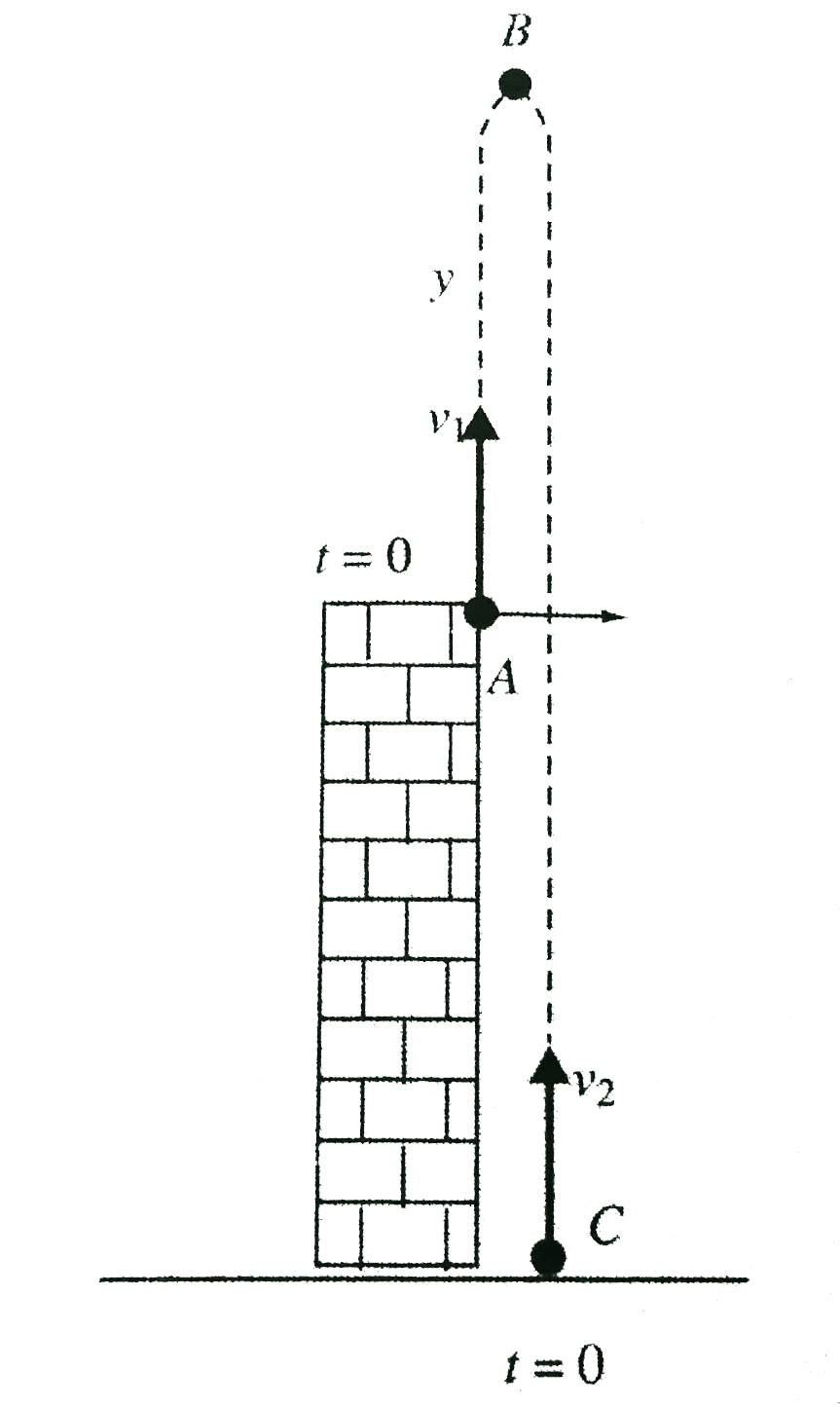 .
.
View SolutionA ball is projected downward from the top of a cliff of height h with an initial speed v.Another ball is simultaneously projected vertically up from the bottommost of the cliff with the same speed.When do they meet?
View Solution
Knowledge Check
A wooden block is dropped from the top of a cliff 100m high and simultaneously a bullet of mass 10 g is fired from the foot of the cliff upwards with a velocity of 100m/s. The bullet and wooden block will meet each other after a time:
A10 sB0.5 sC1 sD7 s
Two bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10 and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.
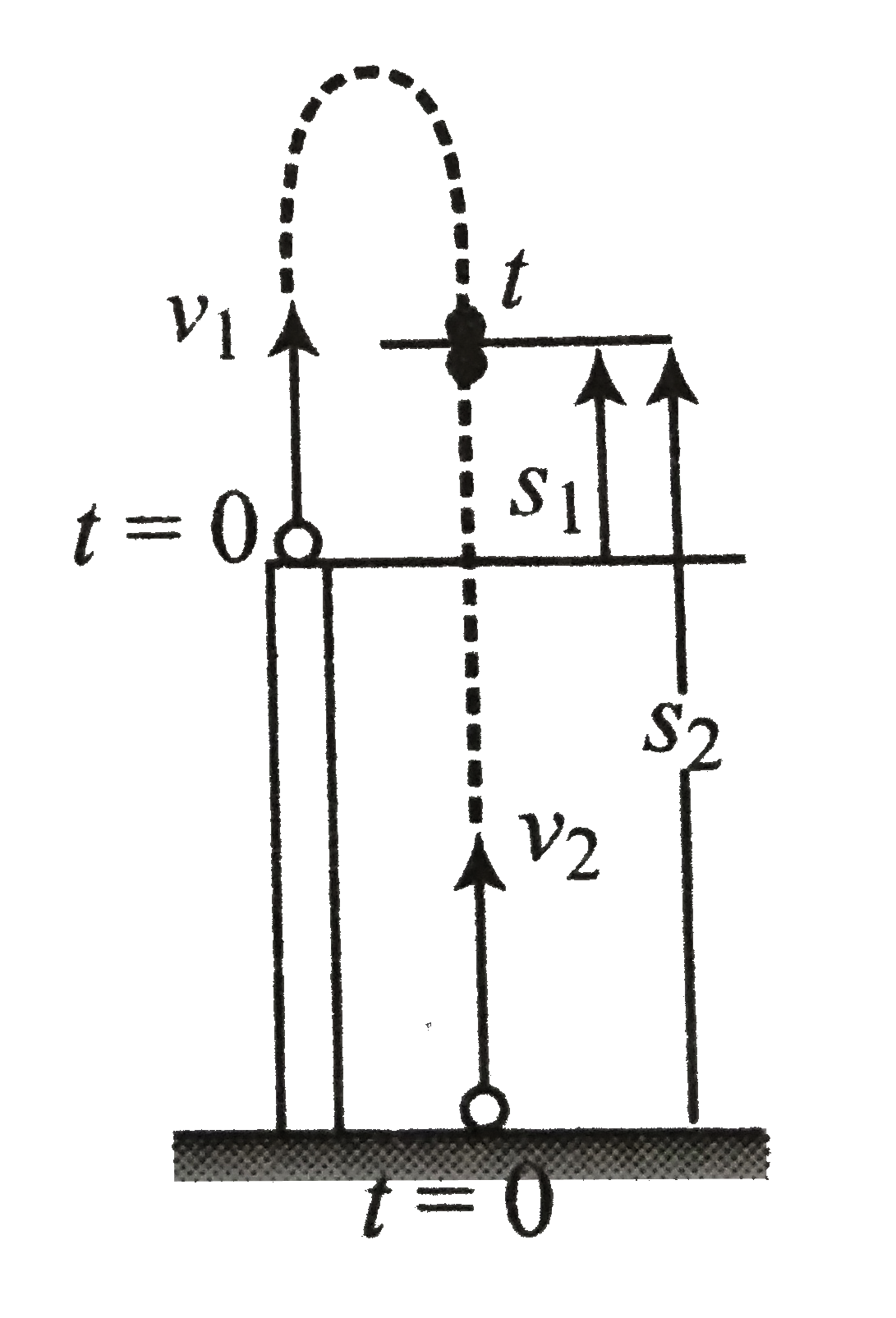
View SolutionA man on the deck of a ship is 10m above the water level. He observes that the angle of elevation of the top of a cliff is 45o and the angle of depression of the base is 30o . Calculate the distance of the cliff from the ship and the height of the cliff.
View SolutionA stone is dropped from the top of a cliff of height h. ''n'' seconds later, a second stone is projected downwards from the same cliff with a vertically downward velocity u. Show that the two stones will reach the bottom of the cliff together, if
8h(u−gn)2=gn2(2u−gn)2
what can you say about the limiting value of ''n'' ?
View SolutionA man on the deck of a ship 12 m above water level, observes that the angle of elevation of the top of a cliff is 60∘ and the angle of depression of the base of the is 30∘. Find the distance of the cliff from the ship and the height of the cliff. [use √3=1.732)
View SolutionAman on deck of a ship is 12 m above the water level. He observes that the angle of the elevation of the top of a cliff is 45∘ and the angle of depression of its base is 30∘. Calculate the distance of the cliff from the ship and the height of the cliff.
View SolutionTwo particles are simultaneously projected upwards from the top and bottom of a cliff of height = 20 m. If the speed of one is double that of the other and they meet after a time to 2 second, find their speed of projection.
View SolutionA ball is prouected vertical up from the top of a cliff of height h with a speed v1 Another ball is projected vertically up with a speed v2 from the bottom of the cliff, after a time t0 from the instantof projection of the first ball, When will the balls meet?.
View Solution
