With what minimum speed must a particle be projected from origin so that it is able to pass through a given point (30m,40m) ? Take g=10m/s2
26 m/s
30 m/s
20 m/s
10 m/s
The correct Answer is:b
40=30 tan α−(g(30))22u2(1+tan2α)
For real value of α
(6u2)2≥3600(900+8u2)
⇒u4−800u2≥900,00
(u2−400)2≥25,000
⇒u2−400≥5,00
u2≥900
⇒u≥30m/s
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Comprehension (I)
3 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Comprehension (II)
2 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (subjective)
10 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
A particle is projected from the origin in such a way that it passes through a given point P (a, b} What is the minimum requrired speed to do so?
View SolutionA body is projected from the ground with some speed at some angle with the horizontal. Taking the horizontal and vertical direction to be x and y axis respectively and the point of projection as origin, calculate the minimum speed (in ms−1) of projection so that it can pass through a point whose x and y coordinates are 30 m and 40 m respectively? Take g=10ms−2
View Solution
Knowledge Check
Track OABCD (as shown in figure ) is smooth. What minimum speed has to be given to a particle lying at point A, so that it can reach point C? (take g=10m/s2)
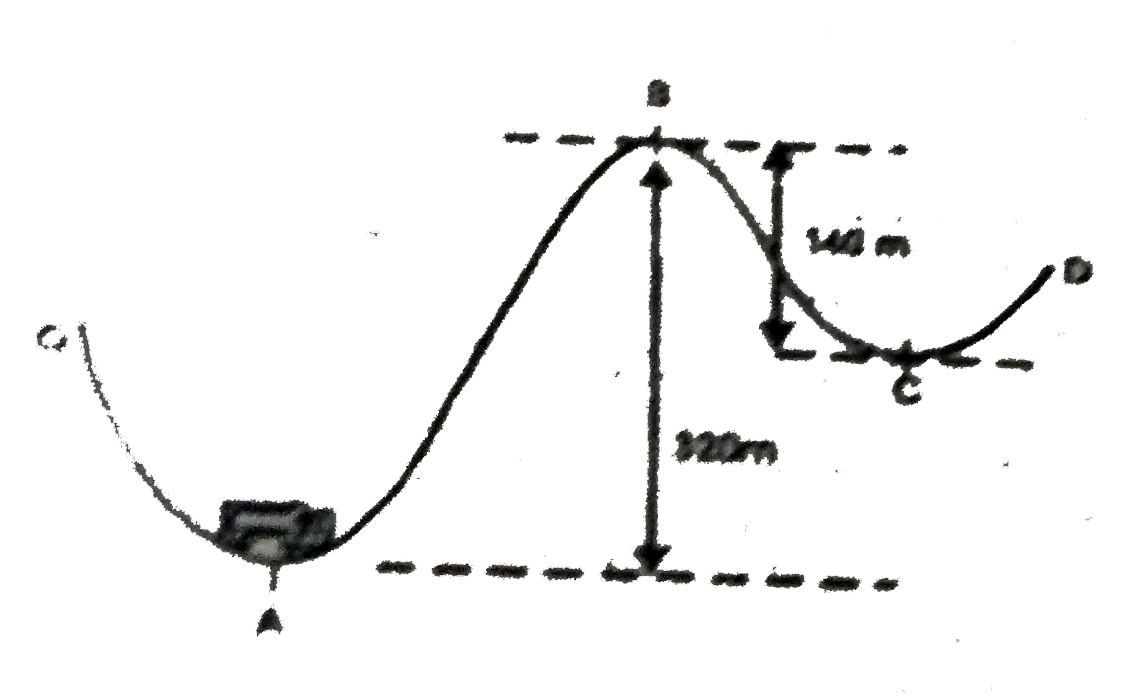 A60 m/sB100 m/sC70 m/sD80m/s
A60 m/sB100 m/sC70 m/sD80m/sA ball is projected vertically up with speed 20 m/s. Take g=10m/s2
AIt covers a distance of 5 m in 2nd second of its motionBThe displacement in 2nd and 3rd second are equalCThe distance covered in 2nd and 3rd second are equalDThe average speed for first 4 seconds is zeroA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
A10mB5mC2.5mD1m
How high must a body be lifted so that it gain P.E. equal to its KE while moving with a velocity of 30m/s?Take g=10m/s2
View SolutionA projectile is projected from top of a wall 20m height with a speed of 10m/s horizontally. Find range (g=10ms2)
View SolutionA particle is projected from ground with velocity 20(√2)m/s at 45∘. At what time particle is at height 15 m from ground? (g=10m/s2)
View SolutionWhat are the two angles of projection of a projectile projected with velocity of 30m/s, so that the horizontal range is 45m. Take, g=10m/s2.
View SolutionA particle is projected at an angle 60∘ with the horizontal with a speed 10m/s. Then, latus rectum is (Take g=10m/s2)

View Solution
