A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
(a) We have tan θ1=α and tan θ2=β
If the car accelerates for t1and decelerates for t2then t1=t2
t1=Vmaxα,t2=Vmaxβ
Where vmax is the Maximum velocity of the car
1α+1β=t1+t2Vmax
or Vmax=αβtα+β
(b)Distance covered in time t is the area under the curve
s=12(Vmax)t=αβt22(α+β)

Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Problem (objective)
14 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - Comprehension (I)
3 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
A car acceleration form rest at a constant rate α for some time, after which it decelerates at a constant rate β, to come to rest. If the total time elapsed is t evaluate (a) the maximum velocity attained and (b) the total distance travelled.
View Solution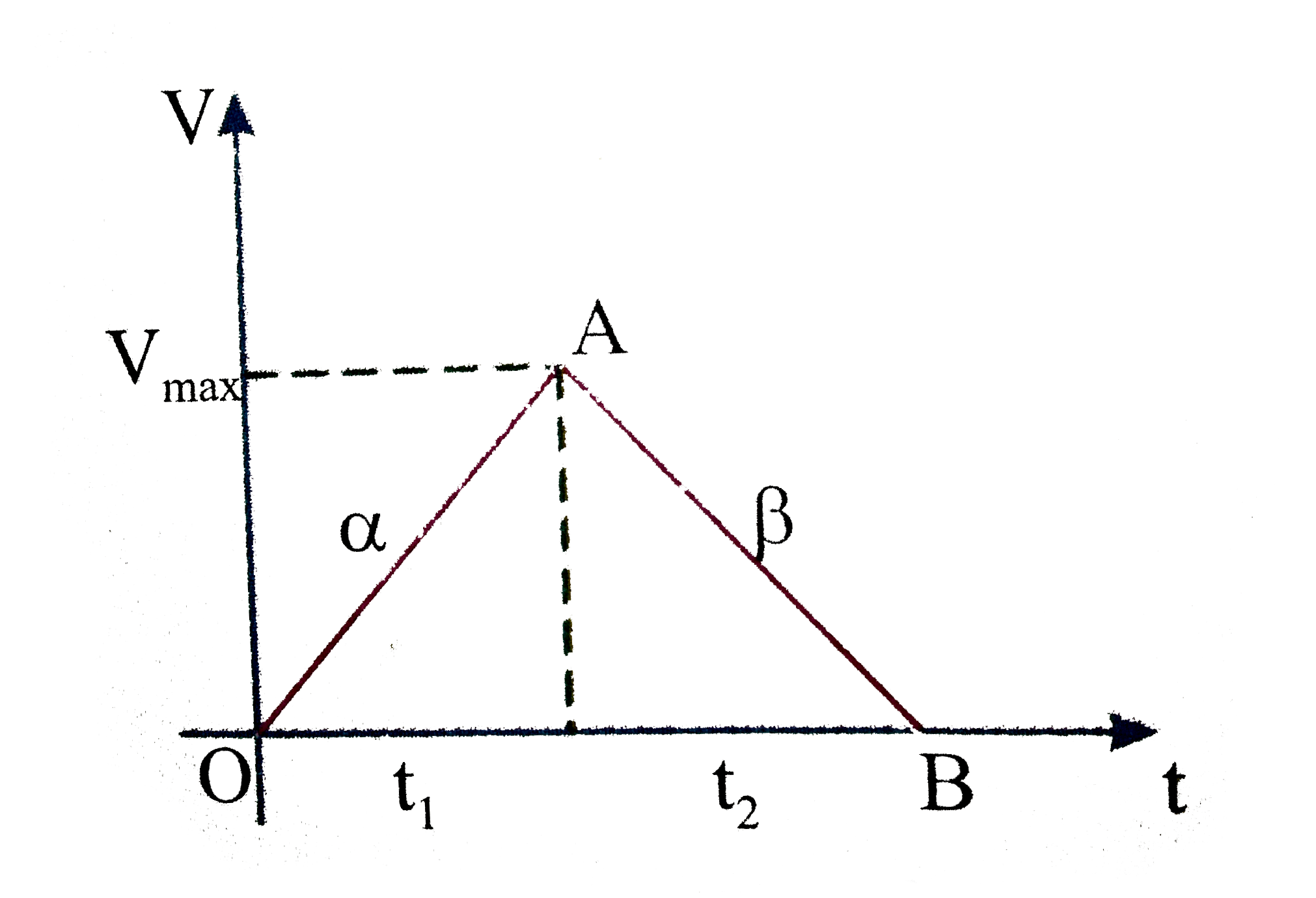
A bus accelerated from rest at a constant rate α for some time, after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t seconds. Then evaluate following parameters from the given graph
(a) the maximum velocity achieved.
(b) the total distance travelled graphically and
(c) Average velocity.
View Solution
Knowledge Check
A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aab(a+b)tBab(a−b)tCat2(a+b)Dtb2(a+b)A car accelerates from rest at a constant rate for some time after which it decelerates at a constant rate β to come to rest. If the total time elapsed is t, the maximum velocity acquired by the car is given by :
Aαβα+βtBα+βαβtCα2+β2βαDα+β2βαA car accelerates from rest at a constant rate α for sometime , after which it decelerates at a constant rate β and comes to rest. If T is the total time elapsed, the maximum velocity acquired by the car is
A(αβα+β)TB((α+βαβ)TC(α2+β2αβ)TD12αTβ
A car accelerates from rest at a constant rate α for some time, after which it decelerates at a constant rate β and ultimately comes to rest.If the total time-lapse is t, what is the total distance described and maximum velocity reached ?
View SolutionA car accelerates from rest at acionstant rate 36kmh∘ to comet to rest. If the total time elapsed id 1 hour, calculate (i) the maximum velocity attained by the car and (ii) the total distance travelled by car.
View SolutionA particle accelerates from rest at a constant rate for some time and attains a velocity of 8 m/sec. Afterwards it decelerates with the constant rate and comes to rest. If the total time taken is 4 sec, the distance travelled is
View SolutionA car accelerates from rest at a constant rate of 2ms−2 for some time. The it retatds at a constant rate of 4ms−2 and comes to rest. It remains in motion for 6s.
View SolutionA car accelerates from rest at constant rate of 2ms−2 for some time. Then it retards at a constant rate of 4ms−2 and comes to rest. It remains in motion for 3 seconds
View Solution
