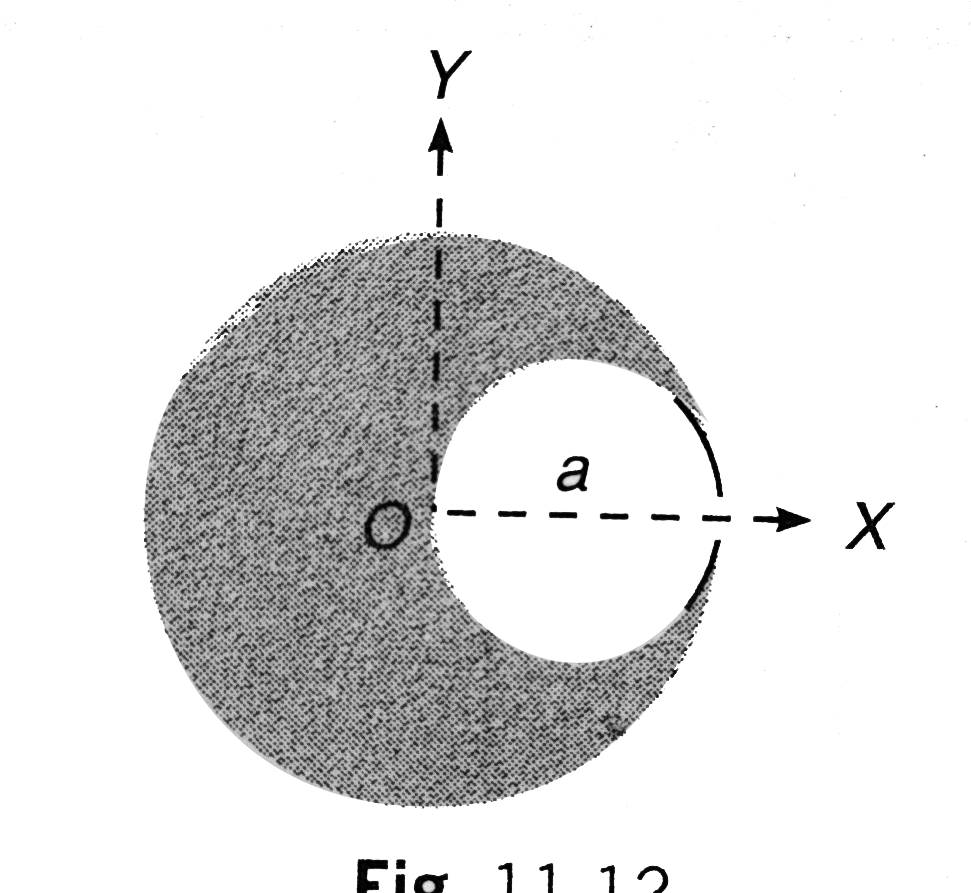
Find the position of center of mass of the uniform lamina shown in figure, if small disc of radius α2 is cut from disc of radius a.
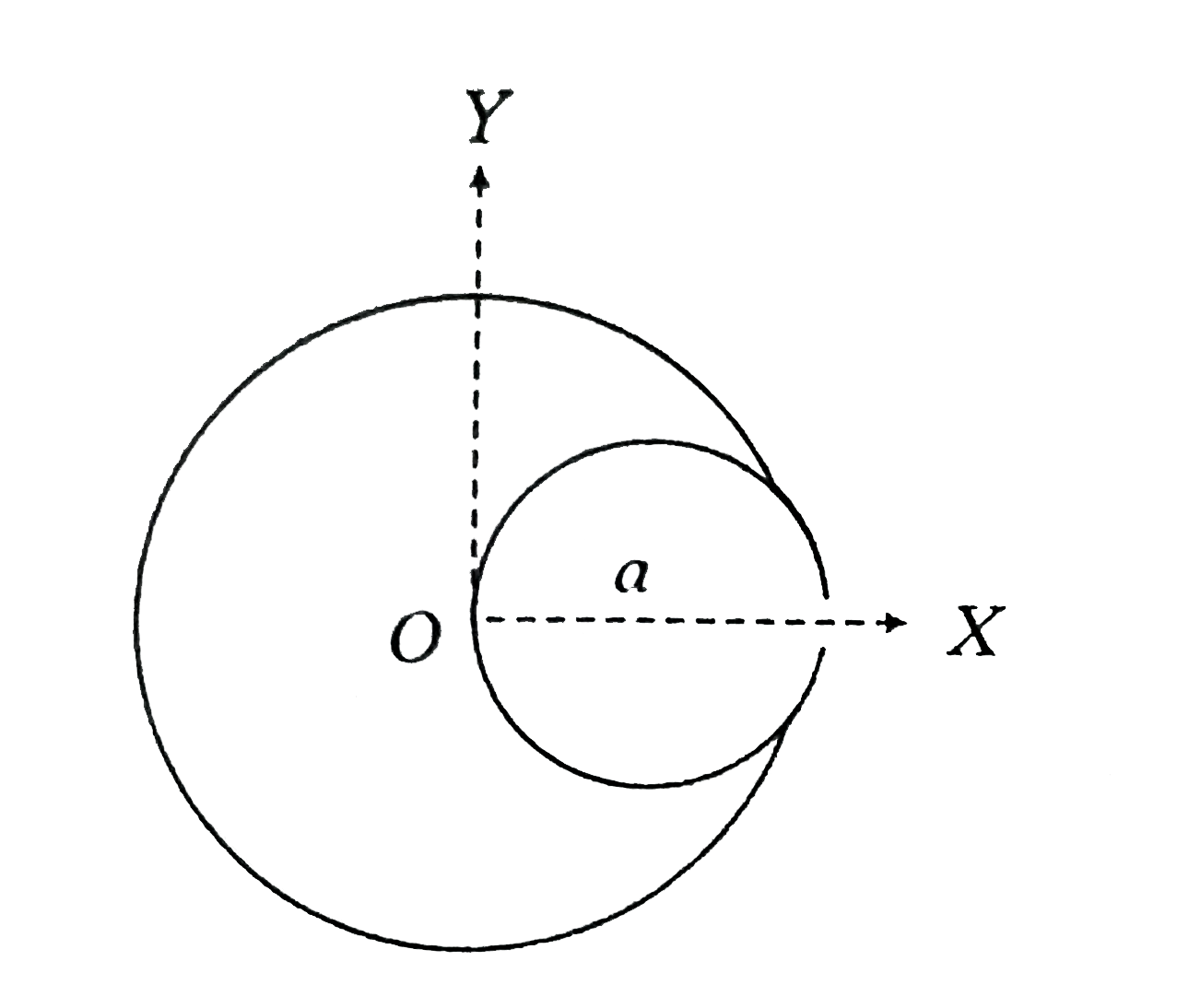
Video Solution
Text Solution
Here, A1 = area of complete circular disc = pia^2 A2 = area of small circular disc =π(a2)2 = πa2(x1,y1) = coordinates of centre of mass of large circular disc = (0, 0) and (x2,y2) = coordinates of centre of mass of small circular disc = (a2,0) Using xcm=A1x1−A2x2A1−A2 We get xcm=−πa24(a2)πa2−πa24=−1834a=−a6andycm=0asy1andy−2 both are zero. Therefor, coordinatesof CM of the circular disc shown in figure are (-a/6,0)
|
Similar Questions
Knowledge Check
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
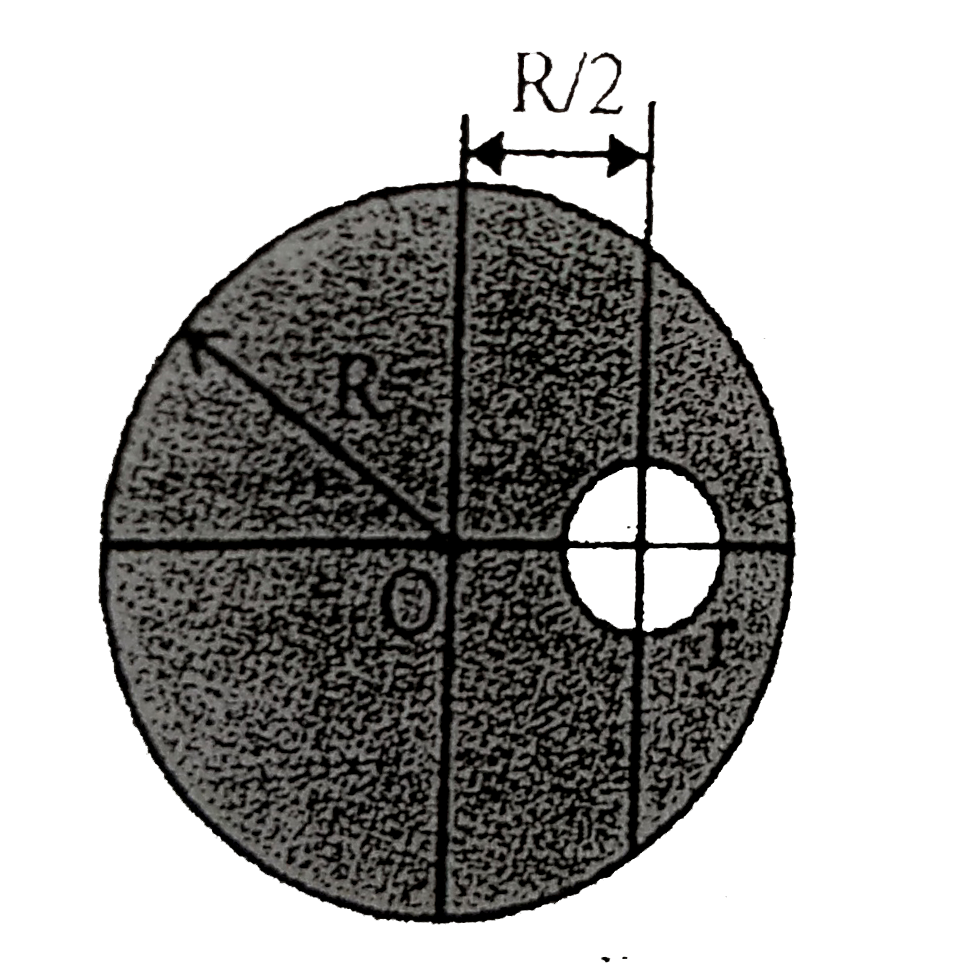 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of OFind moment of inertia of half disc of radius R2 and mass M about its centre. A smaller half disc of radius R1 is cut from this disc
 AM4(R21+R22)BM8(R21+R22)CM16(R21+R22)DM32(R21+R22)
AM4(R21+R22)BM8(R21+R22)CM16(R21+R22)DM32(R21+R22)Given a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
A3MR2/32B5MR2/16C1MR2/64Dnone of these
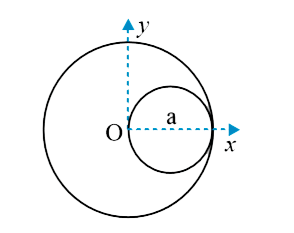
Find out the position of centre of mass of the uniform lamina as shown in figure.from center of cavity
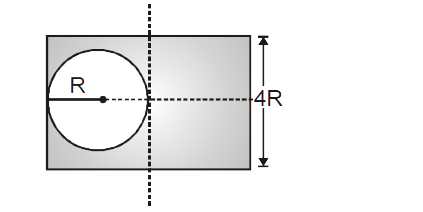
View SolutionFind the position of centre of mass of the uniform lamina shown in figure. If the mass density of the lamina is σ.

View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View SolutionFind the centre of mass of the disc shown in figure. . A square is removed from the disc as shown
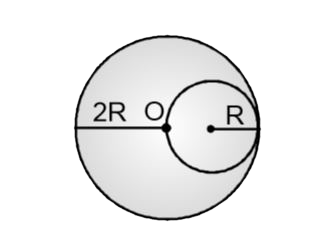
View SolutionA uniform disc having radius 2R and mass density σ as shown in figure. If a small disc of radius R is cut from the disc as shown. Then find out the moment of inertia of remaining disc around the axis that passes through O and is perpendicular to the plane of the page.
View Solution