A uniform disc having radius 2R and mass density $σ$ as shown in figure. If a small disc of radius R is cut from the disc as shown. Then find out the moment of inertia of remaining disc around the axis that passes through O and is perpendicular to the plane of the page.

Video Solution

Text Solution

Verified by Experts

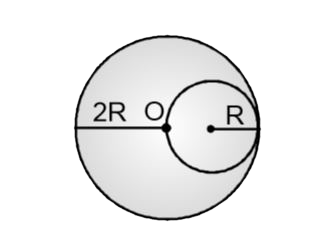
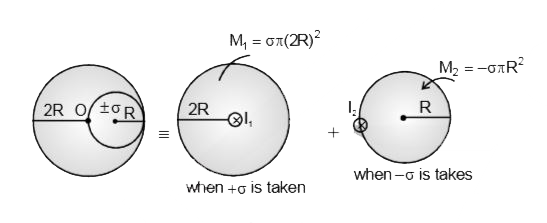
We assume that in remaning part a dise of radius R and mass density $\pm σ$ is placed . Then
Total Moment of Inertia $I = I_{1} + I_{2}$
$I_{1} = \frac{M_{1} {(2 R)}^{2}}{2}$
$I_{1} = \frac{σ π 4 R^{2} 4 R^{2}}{2} = 8 π σ R^{4}$
To calculate $I_{2}$ we use parallel axis theorem .
$I_{2} = I_{C M} + M_{2} R^{2}$
$I_{2} = \frac{M_{2} R^{2}}{2} + M_{2} R^{2}$
$I_{2} = \frac{3}{2} M_{2} R^{2} = \frac{3}{2} (- σ π R^{2}) R^{2} I_{2}$
$= - \frac{3}{2} σ π R^{4}$
Now $I = I_{1} + I_{2}$
$I = 8 π σ R^{4} = \frac{3}{2} σ π R^{4}$
$I = \frac{13}{2} σ π R^{4}$

Updated on:21/07/2023

The moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is
A $(M R^{2}$
B $\frac{3}{2} M R [^(2)$
C $\frac{M R^{2}}{2}$
D $\frac{5}{4} M R^{2}$
From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed as shown in figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

A $4 M R^{2}$
B $\frac{40}{9} M R^{2}$
C $40 M R^{2}$
D $\frac{37}{9} M R^{2}$
From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

A $4 M^{2}$
B $\frac{40}{9} M R^{2}$
C $10 M R^{2}$
D $\frac{37}{9} M R^{2}$