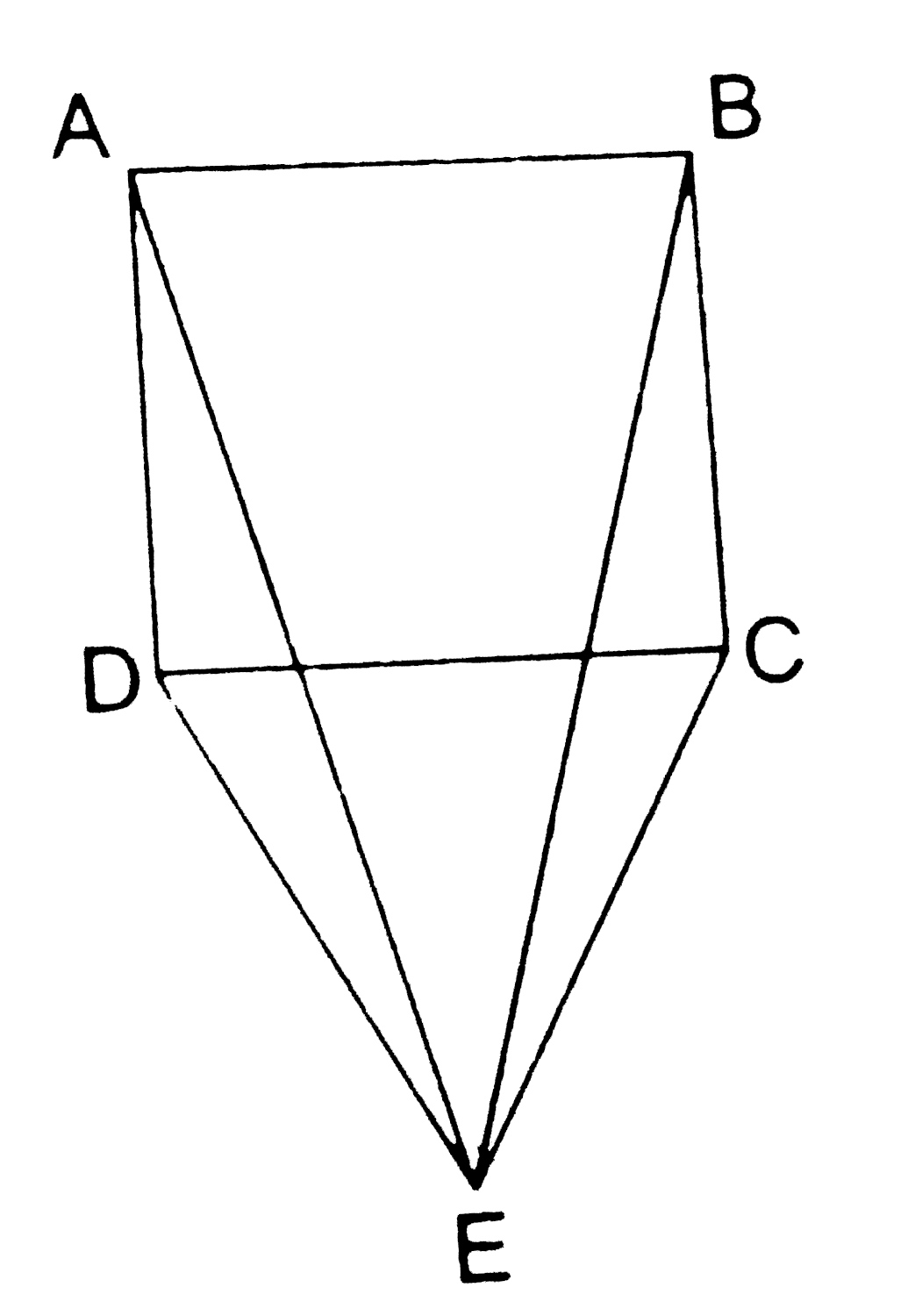
In the given figure,ΔCDE is an equlatel triangle triangle formed on a side CD of a square ABCD.Show that ΔADE≅ΔBCE.
Video Solution
Text Solution
Given in figure ΔCDE is an equilateral triangle formed on a side CD of a square ABCD.
To show ΔADE≅ΔBCE
Proof in ΔADEandΔBCE, DE=CE [sides of an equliateral triangle]
∠ADE=∠BCE
⎡⎢
⎢
⎢⎣∵∠ADC=∠BCD=90∘and∠EDC=∠ECD=60∘∴∠ADE=90∘+60∘=150∘and∠BCE=90∘+60∘=150∘⎤⎥
⎥
⎥⎦
and AD=BC [sides of a square]
∴ ΔADE≅ΔBCE [by SAS congruence rule ]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
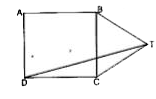
In the given diagram, ABCD is a square and Δ BCT is an equilateral triangle. ∠ BTD equals
 A30∘B15∘C45∘D35∘
A30∘B15∘C45∘D35∘An equilateral triangle CDE is constructed on a side CD of sqaure ABCD. The measure of ∠AEB can be __________.
A150∘B45∘C30∘D20∘In the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.
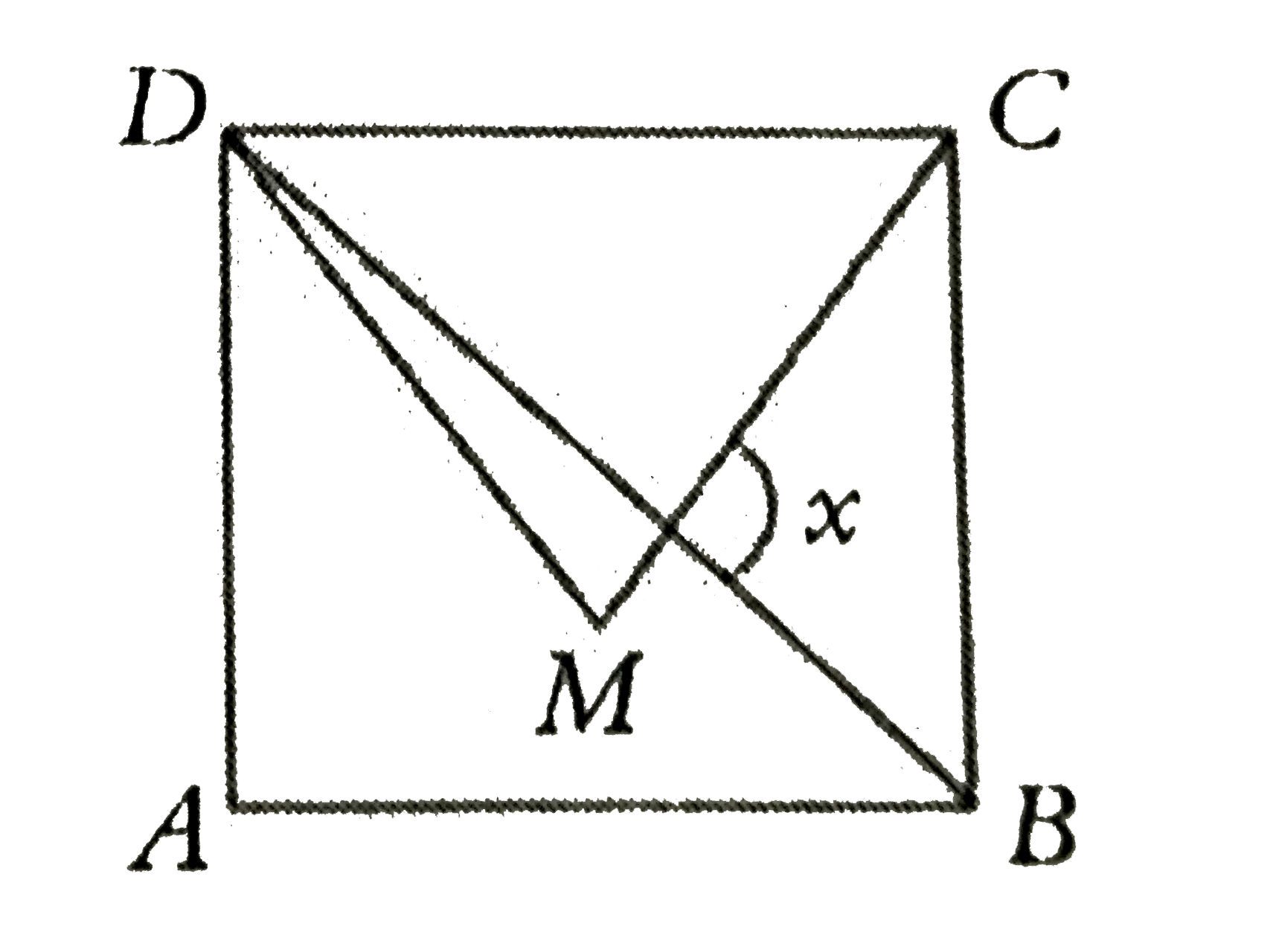 A75∘B90∘C105∘D60∘
A75∘B90∘C105∘D60∘
In the given figure, ABCD is a square and ΔBCT is an equilateral triangle. Find ∠BTD.
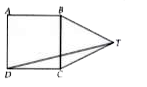
View SolutionObserve the given figure :
Say the sides of the triangle.
View SolutionIn the given figure equilateral triangle EDC surmounts the square ABCD. α=
View SolutionIn the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.

View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP Calculate
View Solution