CDE
is an equilateral
triangle formed on a side CD
of a square ABCD.
Show that ADE ≅BCE.
To show that triangle ADE is congruent to triangle BCE, we will use the SAS (Side-Angle-Side) congruence criterion. Here’s a step-by-step solution:
Step 1: Identify the Given Information
We have a square ABCD and an equilateral triangle CDE formed on side CD.
Step 2: Analyze the Angles
Since CDE is an equilateral triangle, all its angles are 60∘. Therefore:
- ∠DCE=60∘
- ∠CDE=60∘
Also, since ABCD is a square, we know:
- ∠DAB=90∘
- ∠ABC=90∘
Step 3: Find the Angles in Triangles ADE and BCE
Now, we can find the angles in triangles ADE and BCE:
- In triangle ADE:
∠ADE=∠DAB+∠DCE=90∘+60∘=150∘
- In triangle BCE:
∠BCE=∠ABC+∠CDE=90∘+60∘=150∘
Step 4: Identify the Sides
Next, we identify the lengths of the sides:
- AD is a side of the square ABCD.
- BC is also a side of the square ABCD.
- Since ABCD is a square, we have:
AD=BC
- DE is a side of the equilateral triangle CDE.
- CE is also a side of the equilateral triangle CDE.
- Since CDE is equilateral, we have:
DE=CE
Step 5: Apply the SAS Criterion
Now we have:
1. AD=BC (sides of the square)
2. DE=CE (sides of the equilateral triangle)
3. ∠ADE=∠BCE=150∘
By the SAS criterion, we can conclude that:
△ADE≅△BCE
Conclusion
Thus, we have shown that triangle ADE is congruent to triangle BCE using the SAS criterion.
---
We have a square ABCD and an equilateral triangle CDE formed on side CD.
Since CDE is an equilateral triangle, all its angles are 60∘. Therefore:
- ∠DCE=60∘
- ∠CDE=60∘
- ∠DAB=90∘
- ∠ABC=90∘
Now, we can find the angles in triangles ADE and BCE:
- In triangle ADE:
∠ADE=∠DAB+∠DCE=90∘+60∘=150∘
- In triangle BCE:
∠BCE=∠ABC+∠CDE=90∘+60∘=150∘
Next, we identify the lengths of the sides:
- AD is a side of the square ABCD.
- BC is also a side of the square ABCD.
- Since ABCD is a square, we have:
AD=BC
- CE is also a side of the equilateral triangle CDE.
- Since CDE is equilateral, we have:
DE=CE
Now we have:
1. AD=BC (sides of the square)
2. DE=CE (sides of the equilateral triangle)
3. ∠ADE=∠BCE=150∘
△ADE≅△BCE
Thus, we have shown that triangle ADE is congruent to triangle BCE using the SAS criterion.
Topper's Solved these Questions
Similar Questions
p AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionIn an equilateral triangle ABC if AD⊥BC, then AD2 = (a)CD2 (b) 2CD2 (c) 3CD2 (d) 4CD2
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=12ar(BAE)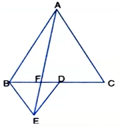
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
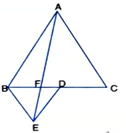
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=14ar(ABC)
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F Prove that: ar(FED)=18ar(AFC)
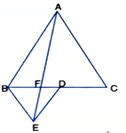
View SolutionIn Figure, ABC and BDE are two equilateral triangls such that D is the mid-point of BC.AE intersects BC in F. Prove that: ar ( BFE)= 2 ar (EFD)
View SolutionAny point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
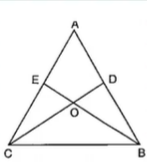
View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View Solution

