D, E, F
are the mid-point of
the sides BC, CA and AB
respectively of ABC.
Then DEF
is congruent to
triangle.
ABC
(b) AEF (c)
BFD, CDE
(d)
AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
Solution : FE=BD(mid-point theorem)
CD=DB(since D is the midpoint of BC)
Now in △sAFEandDEF
FE is common in both the triangles
DF=AE(from the mid-point theorem)
DE=AF(from the mid-point theorem)
This shows that triangles DEF and AFE are congruent to each other by SSS congruence.
Triangles DEF and BFD are also congruent to each other by SSS congruence.
△sDEFandCDE can be shown congruent to each other in a similar way by SSS congruence.
Hence , option (d) is correct.
Topper's Solved these Questions
Similar Questions
D, E, F are the mid-points of the sides BC, CA and AB respectively of a ABC . Determine the ratio of the areas of DEF and ABC .
View SolutionIf D,E,F are the mid-points of the sides BC,CAandAB respectively of a triangle ABC, prove by vector method that AreaofDEF=14(areaofABC).
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
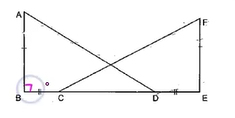 View Solution
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of aΔABC.Show that (i) BDEF is a parallelogram. (ii) ar (DEF)=14ar (ABC)(iii) ar (BDEF)=12ar (ABC)
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View SolutionLet ABC be an isosceles triangle in which AB=AC If D,E,F be the mid-points of the sides BC, CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
View SolutionIn ΔABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABCis divided into four congruent triangles by joining D, E and F.
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View Solution

