In a ABC,
if AB=AC and BC
is produced to D
such that ∠ACD=1000,
then ∠A=
200
(b) 400
(c)
600
(d)
800
To solve the problem step by step, we will analyze the given information and use properties of triangles.
Step 1: Understand the Given Information
We have a triangle ABC where AB=AC and BC is extended to point D such that ∠ACD=100∘.
Step 2: Identify the Angles
Since AB=AC, triangle ABC is an isosceles triangle. This means that the angles opposite the equal sides are also equal. Therefore, we can denote:
- ∠B=x
- ∠C=x
Step 3: Use the Linear Pair of Angles
We know that ∠ACD and ∠ACB form a linear pair. Thus, we can write:
∠ACB+∠ACD=180∘
Substituting the known value:
x+100∘=180∘
Step 4: Solve for x
Now, we can solve for x:
x=180∘−100∘=80∘
Thus, ∠B=80∘ and ∠C=80∘.
Step 5: Find Angle A
In triangle ABC, the sum of the angles is 180∘:
∠A+∠B+∠C=180∘
Substituting the values we found:
∠A+80∘+80∘=180∘
This simplifies to:
∠A+160∘=180∘
Now, solving for ∠A:
∠A=180∘−160∘=20∘
Conclusion
The value of ∠A is 20∘. Therefore, the correct option is (a) 20∘.
We have a triangle ABC where AB=AC and BC is extended to point D such that ∠ACD=100∘.
Since AB=AC, triangle ABC is an isosceles triangle. This means that the angles opposite the equal sides are also equal. Therefore, we can denote:
- ∠B=x
- ∠C=x
We know that ∠ACD and ∠ACB form a linear pair. Thus, we can write:
∠ACB+∠ACD=180∘
Substituting the known value:
x+100∘=180∘
Now, we can solve for x:
x=180∘−100∘=80∘
Thus, ∠B=80∘ and ∠C=80∘.
In triangle ABC, the sum of the angles is 180∘:
∠A+∠B+∠C=180∘
Substituting the values we found:
∠A+80∘+80∘=180∘
This simplifies to:
∠A+160∘=180∘
Now, solving for ∠A:
∠A=180∘−160∘=20∘
The value of ∠A is 20∘. Therefore, the correct option is (a) 20∘.
Topper's Solved these Questions
Similar Questions
In a ABC, if AB=AC and BC is produced to D such that ∠ACD=1000, then ∠A= 200 (b) 400 (c) 600 (d) 800
View SolutionIn a rhombus ABCD, if ∠ACB=40∘, then ∠ADB=(a) 70∘ (b) 45∘ (c) 50∘ (d) 60∘
View SolutionSide BC of a triangle ABC has been produced to a point D such that ∠1200. If ∠B=12∠A, then ∠A is equal to 800 (b) 750 (c) 600 (d) 900
View SolutionABCD is a cyclic quadrilateral such that ∠ADB=300and ∠DCA=800, the ∠DAB= 700 (b) 1000 (c) 1250 (d) 1500
View SolutionThe diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD=50∘, then ∠DPC= 70∘ (b) 90∘ (c) 80∘ (d) 100∘
View SolutionIn ABC, ∠B=∠C and ray AX bisects the exterior angle ∠DAC.If ∠DAX=700, then ∠ACB= 350 (b) 900 (c) 700 (d) 550
View SolutionIn Figure, if EC∣∣AB, ∠ECD=700AND ∠BDO=200 , then ∠OBD is: 200 (b) 500 (c) 600 (d) 700
View SolutionIf AB, BC and CD are equal chords of a circle with O as centre and AD diameter, then ∠AOB= 600 (b) 900 (c) 1200 (d) none of these
View SolutionLine segments AB and CD intersect at O such that AC∣∣DB. If ∠CAB=450and ∠CDB=550, then ∠BOD= 1000 (b) 800 (c) 900 (d) 1350
View SolutionIn Figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD=1460, find ∠AOB
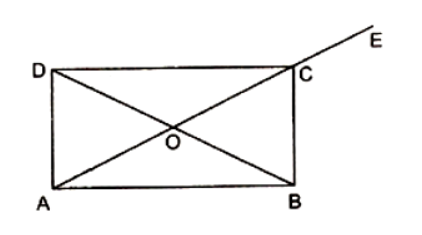
View Solution