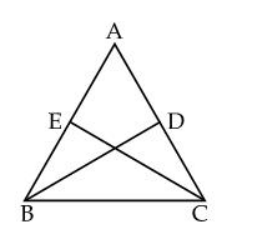
ABC is an isosceles triangle with AB =AC and BD,CE are its two medians. Show that BD=CE .
Given is an isosceles triangle in which AB =AC and BD,CE are its two medians.
To show BD=CE
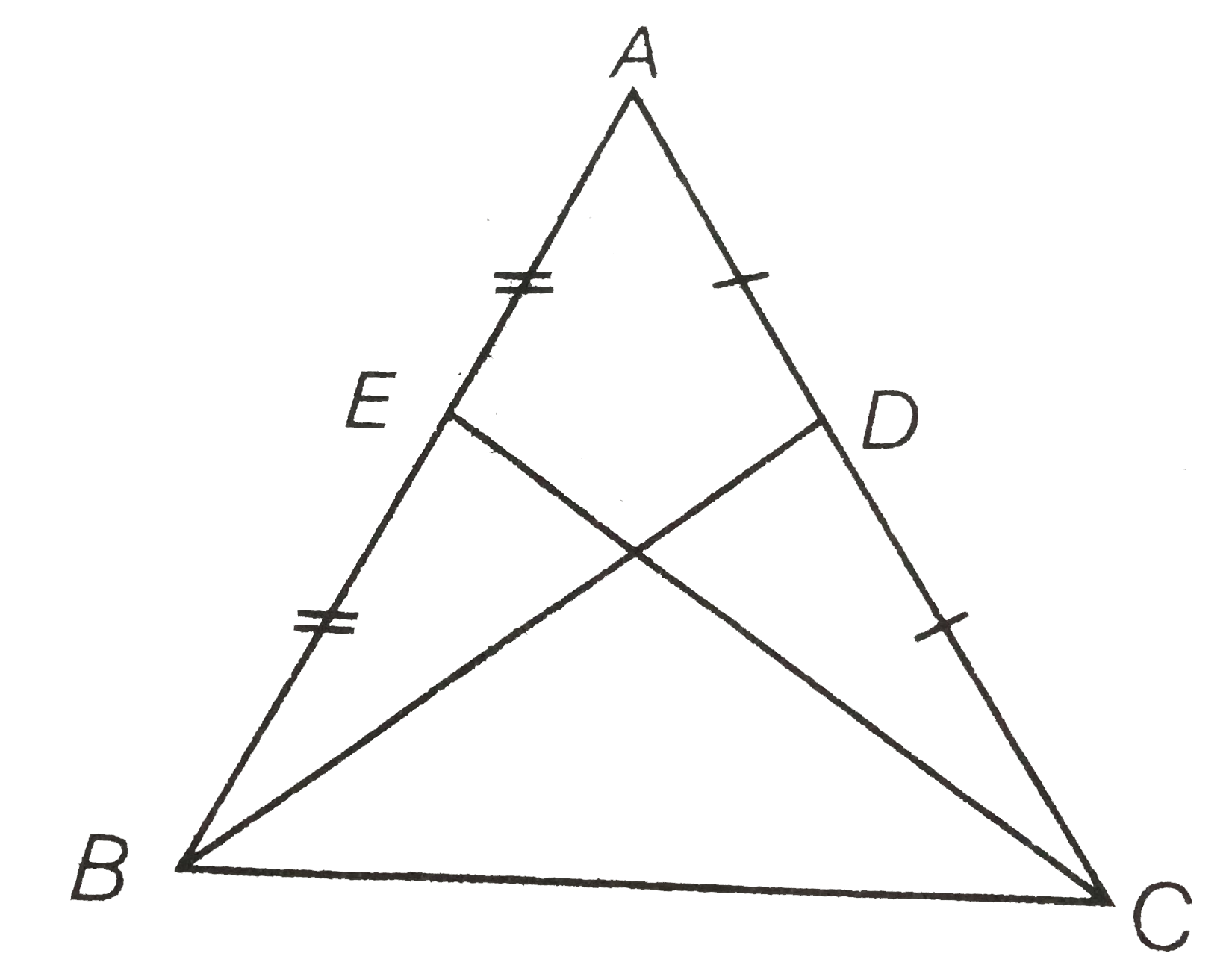
Proof In
and AD=AE
As D is the mid -Point of AC and E is the mid-Point of AB.
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABC is an isosceles triangle such that AB=ACand ADis the median to the base BCwith ∠ABC=35∘ . Then ∠BAD is
A35∘B55∘C70∘D110∘In figure, ABC is a right triangle, right angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD=3√52cm, find the length of CE:
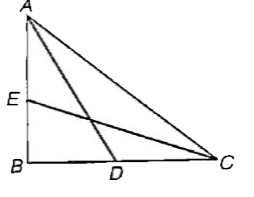 A2√5cmB2.5cmC5cmD4√2cm
A2√5cmB2.5cmC5cmD4√2cm
ABC is an isosceles triangle with AB=AC and D is a point on AC such that BC2=ACxCD. Prove that BD=BC
View SolutionIn the adjoining figure, ABC is an isosceles triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠A and ∠D
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
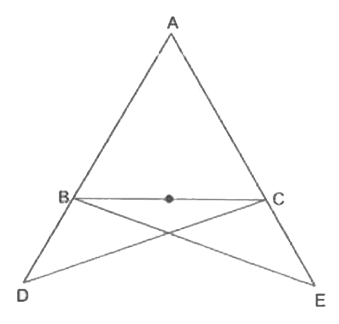
View SolutionIn the given figure, △ABC is an isosceles triangle in which AB - AC. If AB and AC are produced to D and E respectively such that BD = CE, prove that BE = CD. Hint. Show that △ACD=△ABE.
View SolutionΔABC is an isosceles triangle. AB = AC and BD is perpendicular on AC from vertex B, then BD2−CD2 is equal to-
View SolutionLet triangle ABC be an isosceles triangle with AB=AC. Suppose that the angle bisector of its angle B meets the side AC at a point D and that BC=BD+AD. Find angle A (in degrees).
View Solution