Consider a triangle ABC. The sides AB and AC are extended to points D and E respectively, such that AD=3ABandAE=3AC. Then one diagonal of BDEC divides the other diagonal in the ratio p:q then p+q=
Step by step video & image solution for Consider a triangle ABC. The sides AB and AC are extended to points D and E respectively, such that AD = 3AB and AE = 3AC. Then one diagonal of BDEC divides the other diagonal in the ratio p: q then p+q= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
కింది పటంలో ΔABC లో భుజాలు AB,AC లు వరుసగా P,Q బిందువులకు పొడిగించబడినవి. ఇంకనూ ∠PBC<∠QCB. అయిన AC >AB అని చూపండి.
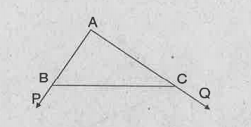 05:08View Solution
05:08View SolutionIn a ΔABC, let P and Q be points on AB and AC respectively such that PQ∣∣BC. Prove that the median AD bisects PQ.
04:48View SolutionIn a parallelogram ABCD, P is the mid point of the side AD. The line BP cuts the diagonal AC in the point Q. Then the ratio AQ:QC=
03:31View SolutionABCD is a parallelogram and P is themid point of the side AD. The line BP meets the diagonal AC in Q. Then the ratio AQ : QC =
02:15View SolutionIn ΔABC, point D and E are the points on sides AB and AC such that AB=5.6, AD=1.4, AC=7.2 and AE=1.8. Show that DE||BC.
03:43View SolutionIn triangle ABC, if P, Q, R divides sides BC, AC, and AB, respectively, in the ratio k:1 (in order). If the ratio (area ΔPQRarea ΔABC) is 13 then k is equal to
06:06View Solutionਚਿੱਤਰ 7.48 ਵਿੱਚ, △ABC ਦੀਆਂ ਭੁਜਾਵਾਂ AB ਅਤੇ AC ਨੂੰ ਕ੍ਰਮਵਾਰ ਬਿੰਦੂਆਂ P ਅਤੇ Q ਤੱਕ ਵਧਾਇਆ ਗਿਆ ਹੈ। ਨਾਲ ਹੀ, ∠PBC<∠QCB ਹੈ। ਦਿਖਾਓ ਕਿ AC > AB ਹੈ।
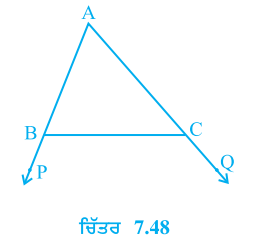 04:04View Solution
04:04View SolutionIn a right triangle ABC right-angled at B, if P and Q are points on the side AB and AC respectively, then___
04:15View Solution
