Two balls A and B of masses 100 gm and 250 gm respectively are connected by a stretched spring of negligible mass and placed on a smooth table. When the balls are released simultaneously the initial acceleration of B is 10 cm/sec2 west ward. What is the magnitude and direction of initial acceleration of the ball A -
25cm/sec2 East ward
25cm/sec2 North ward
25cm/sec2 West ward
25cm/sec2 South ward
The correct Answer is:A
To solve the problem step by step, we will use the concept of the center of mass and the relationship between the accelerations of the two connected masses.
Step 1: Understand the system
We have two balls, A and B, with masses:
- Mass of A (m1) = 100 gm = 0.1 kg
- Mass of B (m2) = 250 gm = 0.25 kg
They are connected by a spring and placed on a smooth table. When released, ball B has an initial acceleration of 10 cm/s² westward.
Step 2: Define the acceleration of the center of mass
The acceleration of the center of mass (a_cm) of a system of particles is given by the formula:
acm=m1a1+m2a2m1+m2
where a1 and a2 are the accelerations of masses A and B respectively.
Step 3: Set up the equation
Given:
- a2=−10cm/s2 (westward is taken as negative)
- acm=0 (since there are no external forces acting on the system)
Substituting the values into the equation for acm:
0=(0.1kg)a1+(0.25kg)(−10cm/s2)0.1kg+0.25kg
Step 4: Simplify the equation
The total mass m1+m2=0.1+0.25=0.35kg.
Now, substituting into the equation:
0=(0.1)a1−2.50.35
Step 5: Solve for a1
Multiplying both sides by 0.35 gives:
0=0.1a1−2.5
Rearranging gives:
0.1a1=2.5
Thus,
a1=2.50.1=25cm/s2
Step 6: Determine the direction
Since a2 was negative (westward), and the system's center of mass must remain stationary, the acceleration of ball A must be in the opposite direction (eastward).
Final Answer
The magnitude of the initial acceleration of ball A is 25 cm/s² and the direction is eastward.
---
We have two balls, A and B, with masses:
- Mass of A (m1) = 100 gm = 0.1 kg
- Mass of B (m2) = 250 gm = 0.25 kg
The acceleration of the center of mass (a_cm) of a system of particles is given by the formula:
acm=m1a1+m2a2m1+m2
where a1 and a2 are the accelerations of masses A and B respectively.
Given:
- a2=−10cm/s2 (westward is taken as negative)
- acm=0 (since there are no external forces acting on the system)
0=(0.1kg)a1+(0.25kg)(−10cm/s2)0.1kg+0.25kg
The total mass m1+m2=0.1+0.25=0.35kg.
0=(0.1)a1−2.50.35
Multiplying both sides by 0.35 gives:
0=0.1a1−2.5
Rearranging gives:
0.1a1=2.5
Thus,
a1=2.50.1=25cm/s2
Since a2 was negative (westward), and the system's center of mass must remain stationary, the acceleration of ball A must be in the opposite direction (eastward).
The magnitude of the initial acceleration of ball A is 25 cm/s² and the direction is eastward.
Topper's Solved these Questions
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-I)
Explore 40 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 2 (Level-II)
Explore 28 Videos
- CENTRE OF MASSBook:MOTIONChapter:CENTRE OF MASSExercise:Exercise - 4 Level-II
Explore 20 Videos
- Capacitance Book:MOTIONChapter:Capacitance Exercise:EXERCISE -4 LEVEL II
Explore 19 Videos
- CIRCULAR MOTIONBook:MOTIONChapter:CIRCULAR MOTIONExercise:EXERCISE - 4
Explore 16 Videos
Similar Questions
Two blocks A and B of masses m and 2m, respectively , are connected by a massless spring of force constant k and are placed on a smooth horizontal plane. The spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is

View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View Solution
Knowledge Check
Two balls A and B of masses 100gm and 250 gm respectively are connected by a stretched spring of negligible mass and placed on a smooth table. When the balls are released simultaneously the initial acceleration of B is 10 cm/sec2 west ward. What is the magnitude and direction of initial acceleration of the ball A-
A25 cm/sec2 EastwardB26 cm/sec2 North wardC27 cm/sec2 West wardD28 cm/sec2 South wardTwo blocks A and With mass 4 kg and 6 kg respectively are connected by a stretched spiring of negligible mass as in figure. When the two blocks are released simultaneously the initial acceleration of B is 1.5m/s2 westward. The acceleration of A is :
 A1m/s2 westwardB2.25m/s2 eastwardC1m/s2 eastwardsD2.75m/s2 westwards
A1m/s2 westwardB2.25m/s2 eastwardC1m/s2 eastwardsD2.75m/s2 westwardsTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correct
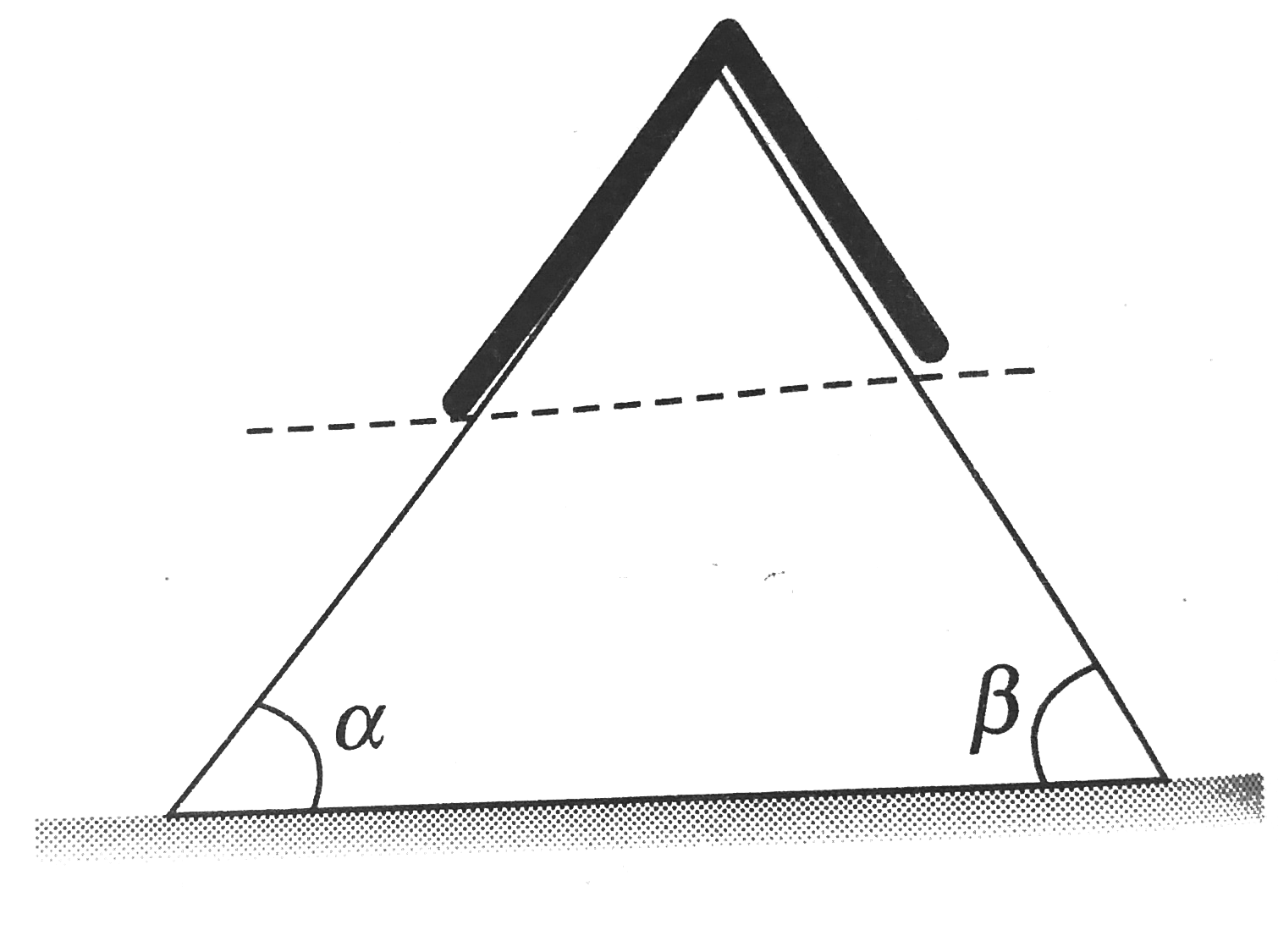
A uniform of rope length L and mass M is placed on a smooth fixed wedge as shown. Both ends of rope are at same horizontal level. The rope is initially released from rest, then the magnitude of initial acceleration of rope is.
View SolutionTwo blocks A and B of masses 2m and respectively, are connected by a massless and inextensible string. The whole system is suspended by a masslessspring as shown in the figure. The magnitude of acceleration of A and B, immediately after the string is cut, are respectively

View SolutionTwo blocks A and B of masses 2m and respectively, are connected by a massless and inextensible string. The whole system is suspended by a masslessspring as shown in the figure. The magnitude of acceleration of A and B, immediately after the string is cut, are respectively

View SolutionTwo blocks A and B of masses 2m and respectively, are connected by a massless and inextensible string. The whole system is suspended by a masslessspring as shown in the figure. The magnitude of acceleration of A and B, immediately after the string is cut, are respectively

View SolutionTwo blocks A and B of masses 3 m and m respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. The magnitudes of acceleration of A and B immediately after the string is cut, are respectively:
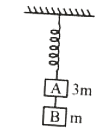
View Solution