A uniform of rope length L and mass M is placed on a smooth fixed wedge as shown. Both ends of rope are at same horizontal level. The rope is initially released from rest, then the magnitude of initial acceleration of rope is.
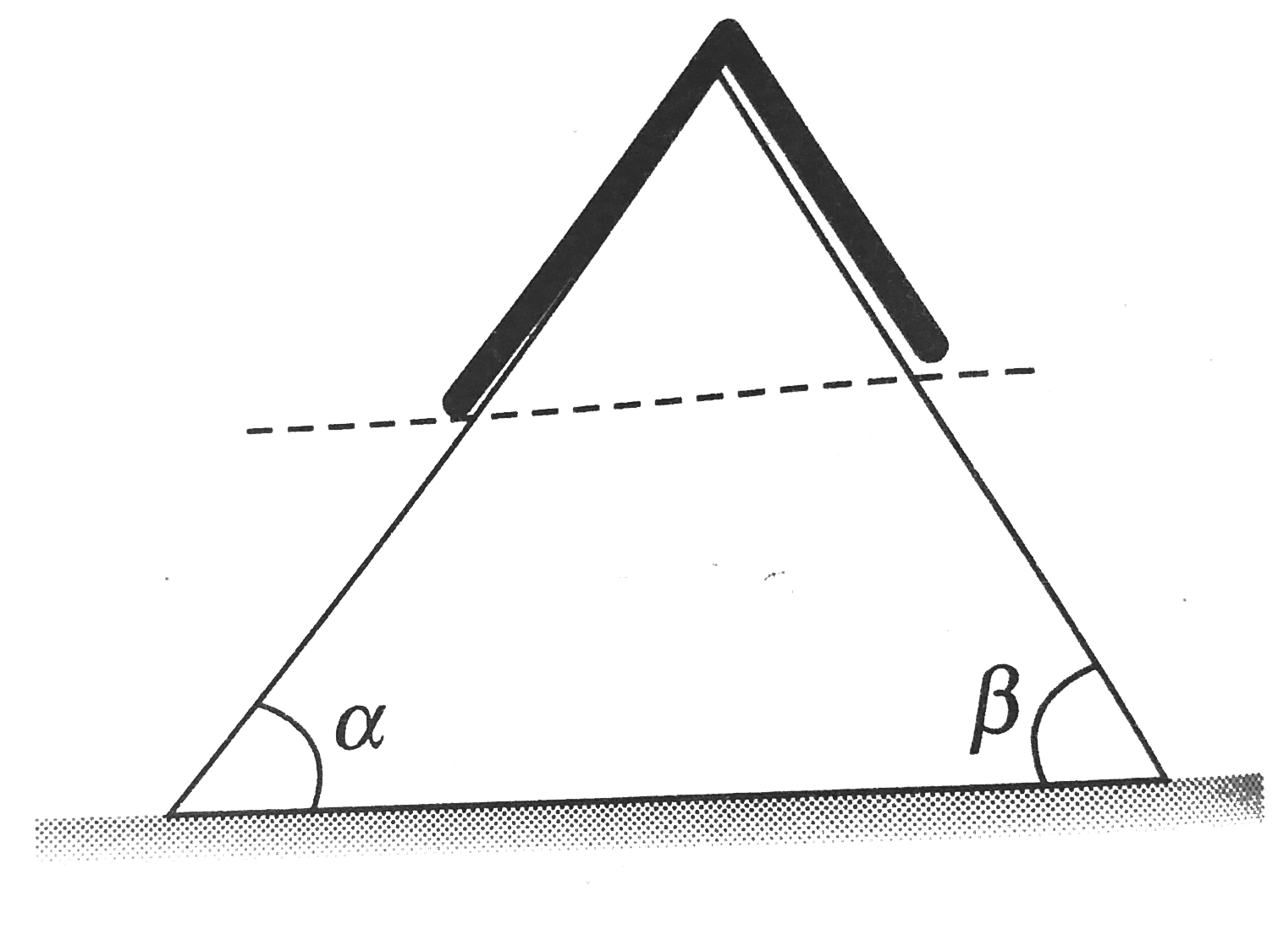
zero
m(cosα−cosβ)g
m(tanα−tanβ)g
none of these
The correct Answer is:A
Let L1 and L2 be the portions (of length) of rope on
left and right surface of wedge as shown :. Magnitude of acceleration of rope a=ML[L1sinα−L2sinβ]gM=0
(:. L1sinα=L2sinβ . 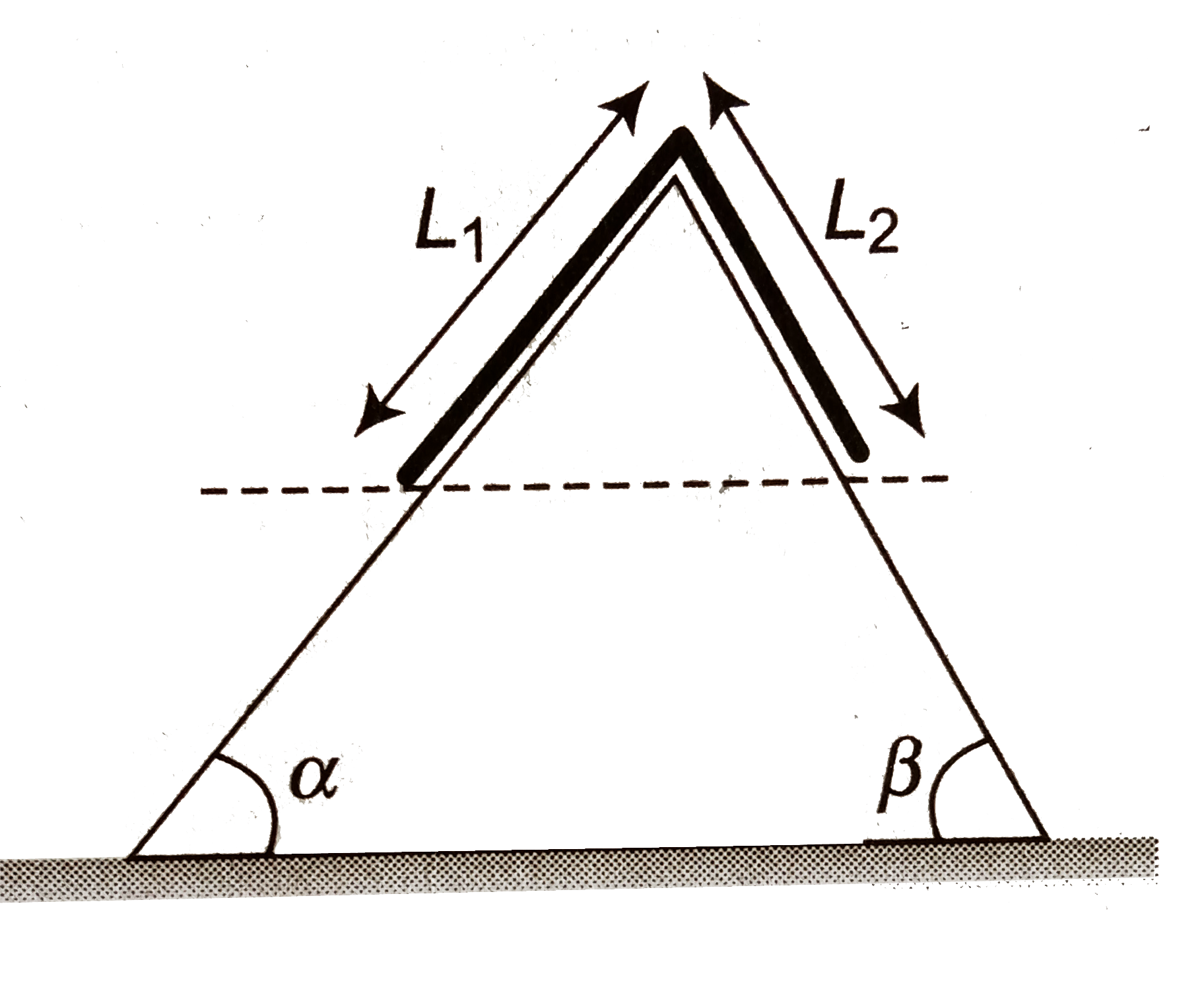
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Basic Concept Of Static And Kinetic Frictions
Explore 45 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Dynamics Of Circular Motion
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Equilibrium Of A Particle
Explore 19 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
A uniform rope of length of length L is pulled by a force F on a smooth surface. Find tension in the rope at a distance x from the end where force is applied.
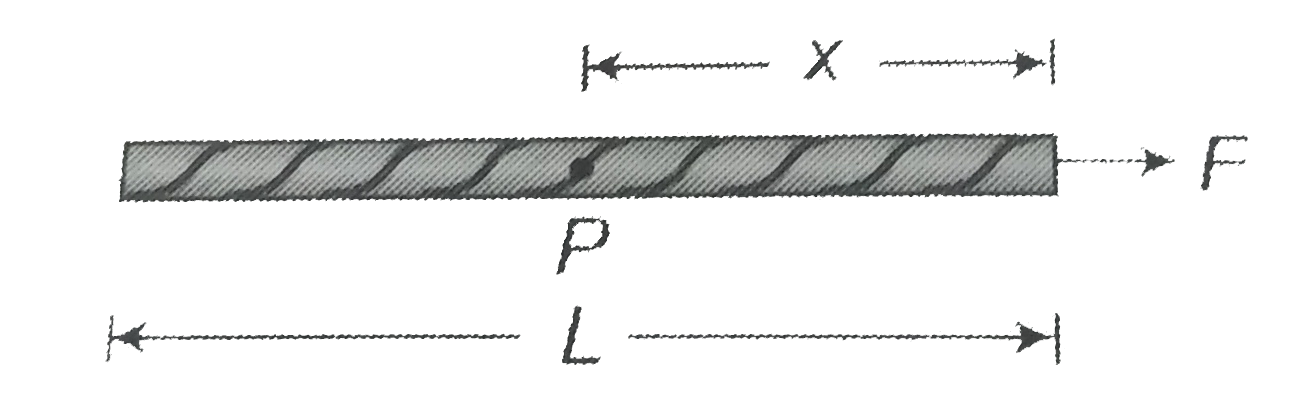
View SolutionA uniform rope of length L is pulled by a constant force F. What is the tension in the rope at a distance l from the end where it is applied?
View Solution
Knowledge Check
A uniform of rope length L and mass M is placed on a smooth fixed wedge as shown. Both ends of rope are at same horizontal level. The rope is initially released from rest, then the magnitude of initial acceleration of rope is.
 AzeroB(cosα−cosβ)gC(tanα−tanβ)gD(sinα−sinβ)g
AzeroB(cosα−cosβ)gC(tanα−tanβ)gD(sinα−sinβ)gA unofrom rope of mass m is placeced on a smooth fixed sphere of radius R as shown in the figure .Find the tension T in the rope when it is in a horizontal plane at a vertical distance h=R/2 below the top of the sphere .
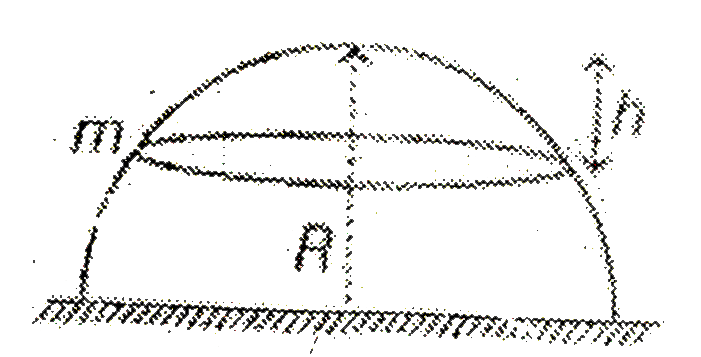 Amg2πBmg2C√3mg2D√3mg2π
Amg2πBmg2C√3mg2D√3mg2πA uniform rope of length l and mass m lies on a smooth horizontal table with its length perpendicular to the edge of the table and a small part of the rope having over the edge. The rope starts sliding from rest under the weight of the over hanging end. The velocity of the rope when the length of the hanging part is . x
A√gxlB√gx2lCgxlDgx2l
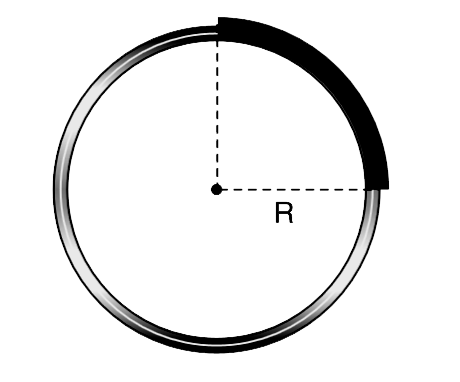
A uniform rope of length πR2 has been placed on fixed cylinder of radius R as shown in the fig. One end of the rope is at the top of the cylinder. The coefficient of friction between the rope and the cylinder is just enough to prevent the rope from sliding. Mass of the rope is M.
(a) At what position, the tension in the rope is maximum?
(b) Calculate the value of maximum tension in the rope.
View SolutionA uniform rope of length L and mass m is held at one end and whirled in a horizontal circle with angular velocity ω .
Ignore gravity. Find the time required for a transverse wave to travel from one end of the rope to the other.
View SolutionA uniform rod of length L and weight W is suspended horizontally by two vertical ropes as shown. The first rope is attached to the left end of the rod while the second is attached to the left end of the rod while the second rope is attached a distance L/4 from the right end. The tension in the second rope is.
 .
.
View SolutionA rope of length L and mass M is being pulled on a rought horizontal floor by a contact horizontal force F=mg. The force is acting at one end of the rope in the same direction as the length of the rop. The coefficient of kinetic friction between rope and floor is 1/2. Then the tension at the midpoint of the rop is
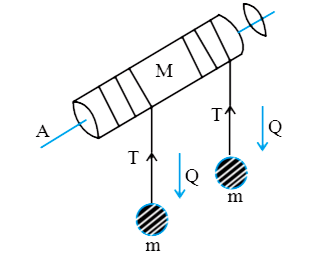
View SolutionA uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
View Solution

