Question

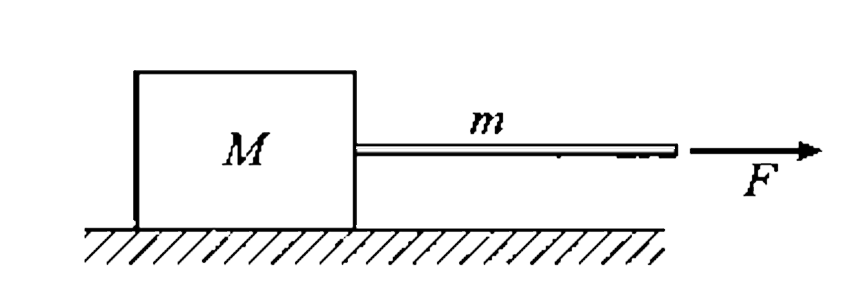
A block of mass $M$ is pulled along a horizontal frictionless surface by a rope of mass $m$ . Force P is applied at one end of rope. The force which the rope exerts on the block is:

Options

A. `(P)/((M-m))`
B. `(P)/(M(m+M))`
C. `(PM)/((m+M))`
D. `(PM)/((M-m))`

Answer

C

Explanation

To solve the problem of finding the force that the rope exerts on the block, we can follow these steps:

Step 1: Understand the System
We have a block of mass \( M \) and a rope of mass \( m \) on a frictionless surface. A force \( P \) is applied to one end of the rope. We need to find the force \( F_b \) that the rope exerts on the block.

Hint: Identify all the components involved, including the applied force, the masses of the block and rope, and the direction of forces.

Step 2: Set Up the Free Body Diagram
Draw a free body diagram for the rope. The forces acting on the rope are:
- The applied force \( P \) acting in the direction of the rope.
- The force \( F_r \) exerted on the rope by the block (which acts in the opposite direction).

Hint: Visualizing the forces will help you understand how they interact with each other.

Step 3: Apply Newton's Second Law to the Rope
According to Newton's second law, the net force acting on the rope is equal to the mass of the rope times its acceleration \( A \). The equation can be written as:
\( P - F_r = m \cdot A \)

Hint: Remember that the net force is the difference between the applied force and the force exerted by the block.

Step 4: Determine the Acceleration of the System
The total mass of the system (block + rope) is \( M + m \). The acceleration \( A \) of the entire system can be expressed as:
\( A = \frac{P}{M + m} \)

Hint: The acceleration is the same for both the block and the rope since they are connected.

Step 5: Substitute Acceleration into the Equation
Substituting \( A \) into the equation from Step 3 gives:
\( P - F_r = m \cdot \frac{P}{M + m} \)

Hint: This substitution allows us to relate the forces directly to the applied force \( P \).

Step 6: Solve for the Force Exerted by the Rope on the Block
Rearranging the equation to solve for \( F_r \):
\( F_r = P - m \cdot \frac{P}{M + m} \)
Factoring out \( P \) gives:
\( F_r = P \left(1 - \frac{m}{M + m}\right) = P \left(\frac{M}{M + m}\right) \)

Hint: Factoring out common terms simplifies the expression.

Step 7: Relate \( F_r \) to \( F_b \)
According to Newton's third law, the force exerted by the rope on the block \( F_b \) is equal in magnitude to the force \( F_r \):
\( F_b = F_r = \frac{M \cdot P}{M + m} \)

Hint: Remember that action and reaction forces are equal and opposite.

Final Answer
The force which the rope exerts on the block is:
\( F_b = \frac{M \cdot P}{M + m} \)