A uniform rope of length L is pulled by a constant force F. What is the tension in the rope at a distance l from the end where it is applied?
To find the tension in a uniform rope of length L being pulled by a constant force F at a distance l from the end where the force is applied, we can follow these steps:
1. Understand the System:
- We have a uniform rope of length L and mass M.
- A constant force F is applied at one end of the rope.
2. Determine the Mass of the Segment:
- The mass per unit length of the rope is given by:
Mass per unit length=ML
- The mass of the segment of the rope from the end where the force is applied to a distance l is:
m′=ML⋅l
3. Apply Newton's Second Law:
- The entire rope accelerates due to the force F. The acceleration a of the rope can be expressed as:
a=FM
4. Consider the Segment of the Rope:
- For the segment of the rope of length l, the net force acting on it can be expressed as:
F−T=m′a
- Here, T is the tension at the distance l from the end where the force is applied.
5. Substituting Values:
- Substitute m′ and a into the equation:
F−T=(ML⋅l)⋅(FM)
- Simplifying this gives:
F−T=F⋅lL
6. Solve for Tension T:
- Rearranging the equation to isolate T:
T=F−F⋅lL
- Factor out F:
T=F(1−lL)
Final Result:
The tension in the rope at a distance l from the end where the force is applied is:
T=F(1−lL)
- We have a uniform rope of length L and mass M.
- A constant force F is applied at one end of the rope.
- The mass per unit length of the rope is given by:
Mass per unit length=ML
- The mass of the segment of the rope from the end where the force is applied to a distance l is:
m′=ML⋅l
- The entire rope accelerates due to the force F. The acceleration a of the rope can be expressed as:
a=FM
- For the segment of the rope of length l, the net force acting on it can be expressed as:
F−T=m′a
- Here, T is the tension at the distance l from the end where the force is applied.
- Substitute m′ and a into the equation:
F−T=(ML⋅l)⋅(FM)
- Simplifying this gives:
F−T=F⋅lL
- Rearranging the equation to isolate T:
T=F−F⋅lL
- Factor out F:
T=F(1−lL)
The tension in the rope at a distance l from the end where the force is applied is:
T=F(1−lL)
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - SWOE
44 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
A uniform rope of length L is pulled by a constant force F. What is the tension in the ropww at a distance l from the end where it is applied?
View SolutionA uniform rope of length L , resting on frictionless horizontal table is pulled at one end by a force F . What is the tension in the rope at a distance x from the end where the force is applied ?
[ Hint : Consider the motion of the entire rope and the motion of x length of rope using P = ma formula and third law of motion ]
View Solution
Knowledge Check
A rope of length 4 m having mass 1.5 kg/m lying on a horizontal frictionless surface is pulled at one end by a force of 12N. What is the tension in the rope at a point 1.6 m from the other end?
A5NB4.8NC7.2ND6NA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
AZeroBF should be equal to the weight of A and BCF(L-x)/LDF(L-x)M
A uniform rope of length of length L is pulled by a force F on a smooth surface. Find tension in the rope at a distance x from the end where force is applied.
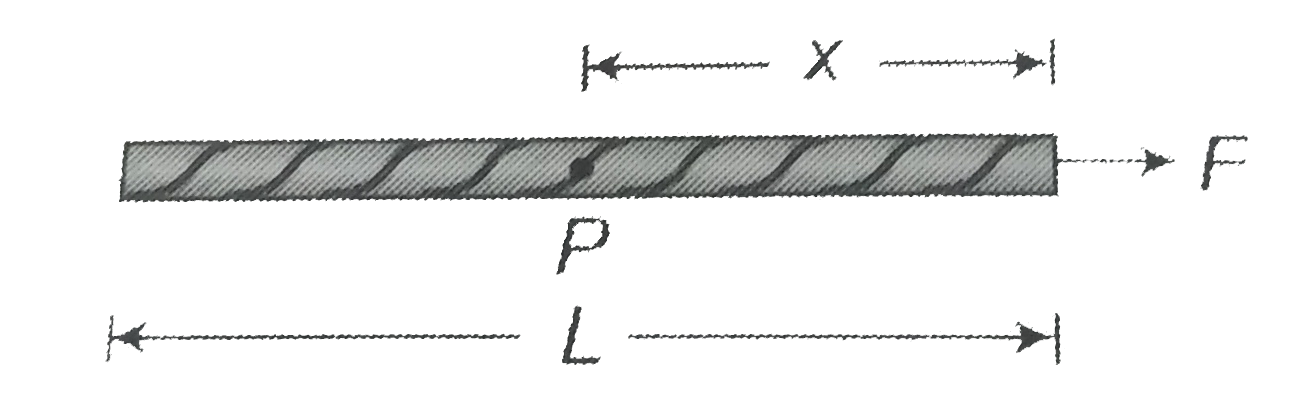
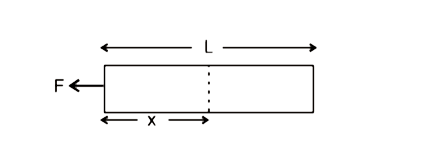
View SolutionA horizontal force is applied on a uniform rod of length L kept on a frictionless surface. Find the tension in rod at a distance 'x' from the end where force is applied
View SolutionA uniform rope of mass M and length L, on which a force F is applied at one end, then find stress in the ropw at a distance x form the end where force is applied?
View SolutionA heavy block of mass M hangs in equilibrium at the end of a rope of mass m and length l connected to a celling. Determine the tension in the rope at a distance x from the ceiling.
View SolutionA homogeneous rod of length L is acted upon by two forces F1andF2 applied to its ends and directed opposite to each other. With what force F will the rod be stretched at the cross section at a distance l from the end where F1 is applied?
View SolutionA uniform rope of mass m and length L is attached to the ceiling of a lift. The other end of the rope is attached to a block of mass M. The lift is moving up with a constant acceleration a0. Find the tension in the rope at a distance x from the ceiling as shown in the diagram.

View Solution
