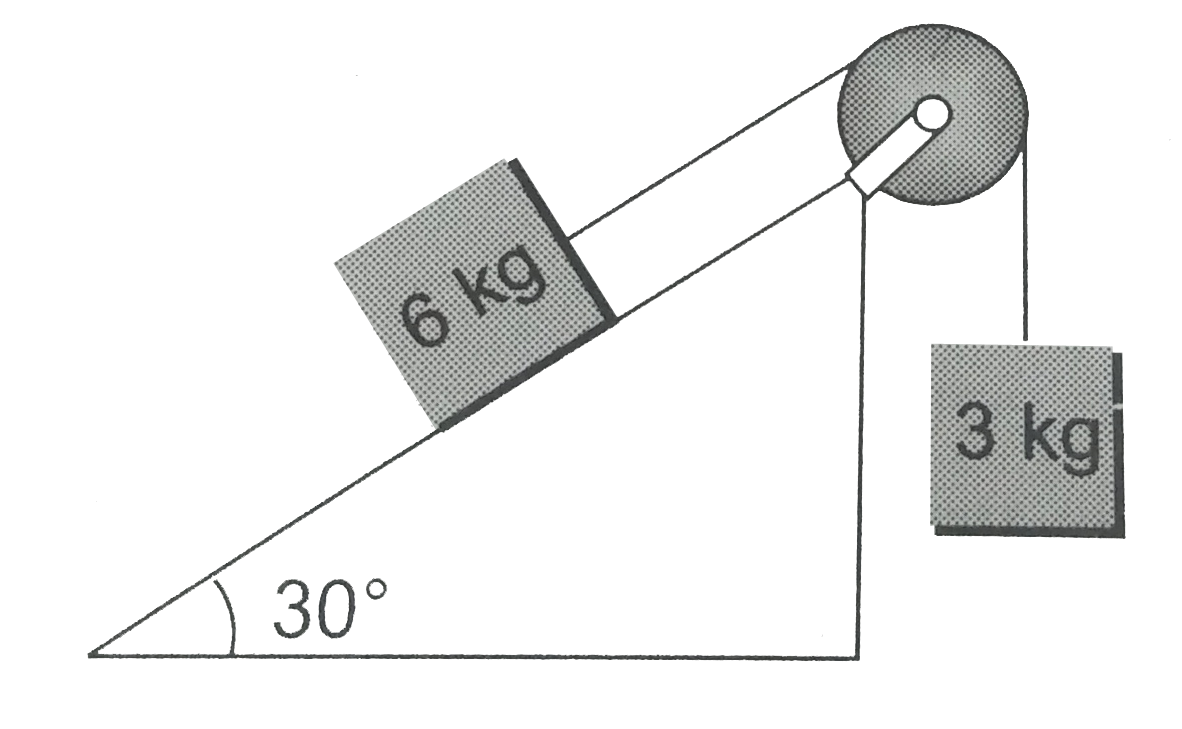
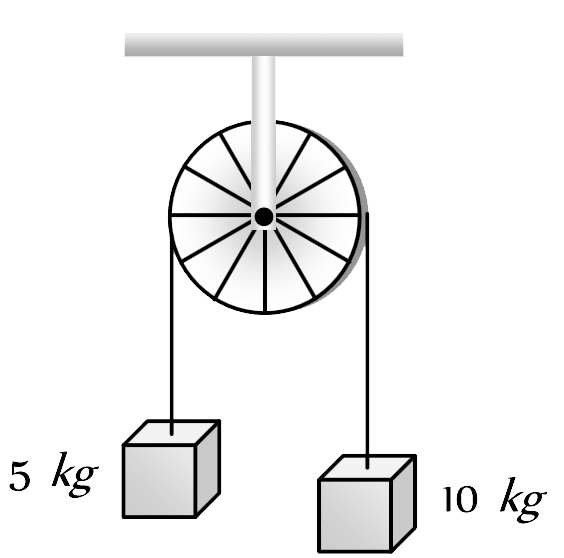
USS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
A
g
B
g/2
C
g/3
D
g/4
Video Solution
Text Solution
The correct Answer is:C
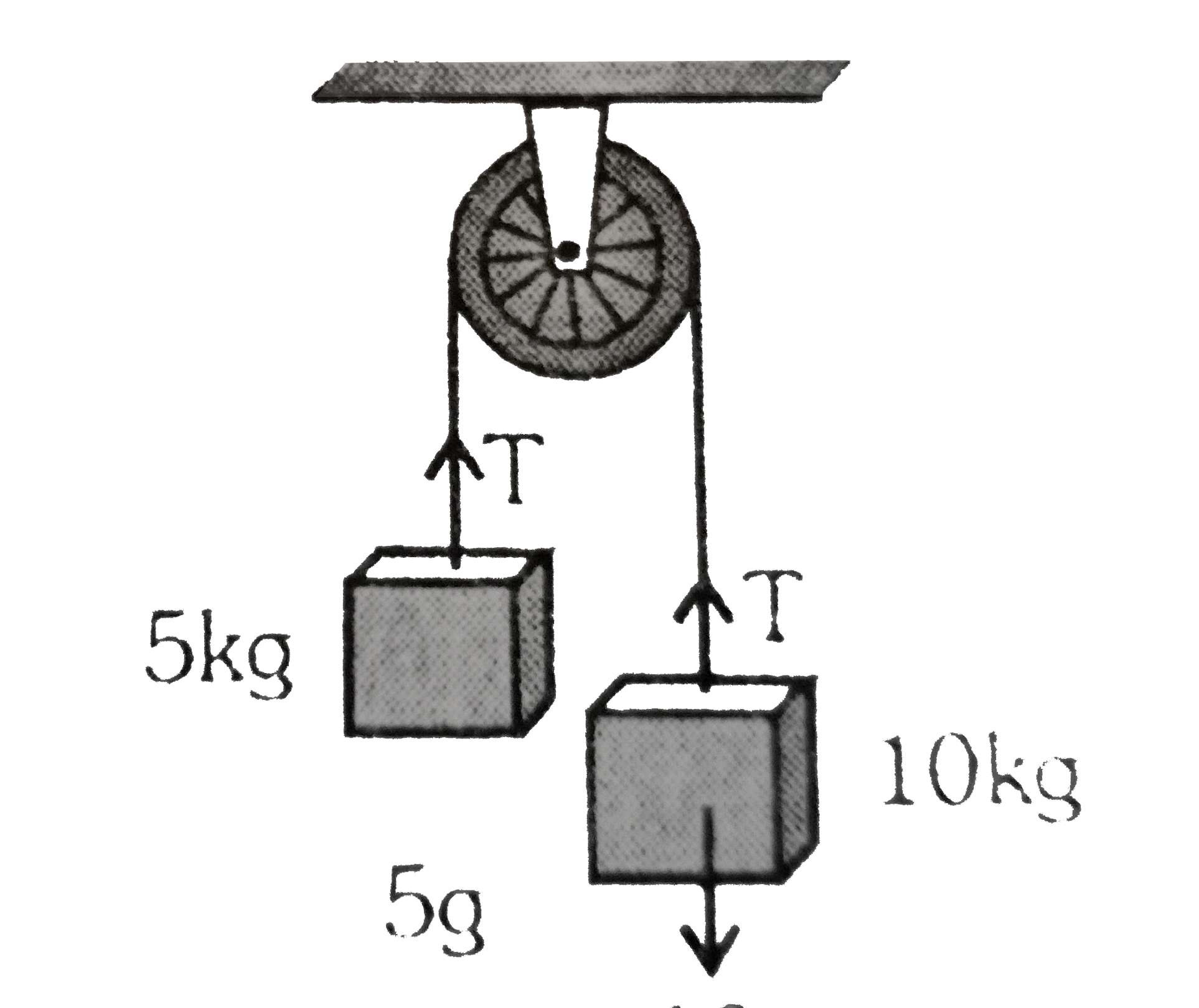
10g−T=10a
T-5g=5a
Solving a=g3
|
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-II
Explore 112 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:SWOE
Explore 44 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
Similar Questions
Knowledge Check
USS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
 AgBg4C4g9D5g9
AgBg4C4g9D5g9Two masses of 8kg and 4kg are connected by a string as shown in figure over a frictionless pulley.The acceleration of the system is
 A4m/s2B2m/s2CzeroD9.8m/s2
A4m/s2B2m/s2CzeroD9.8m/s2Two masses of 8 kg and 4 kg are connected by a string as shown in figure over a frictionless pulley. The acceleration of the system is
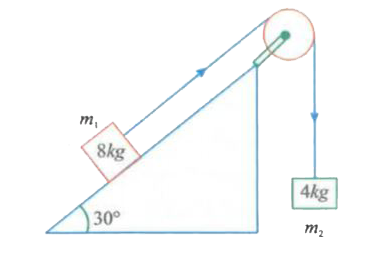 A4m/s2B2m/s2CzeroD9.8m/s2
A4m/s2B2m/s2CzeroD9.8m/s2
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

View SolutionIn the system shown in the figure the acceleration of 1kg mass is
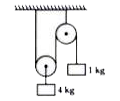
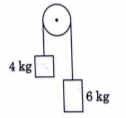
View SolutionTwo bodies of mass 4 kg and tied to the ends of a massless string. the string passes over a pully which is frictionless (see figure). the acceleration of the system in terms of acceleration due to gravity (g) is:
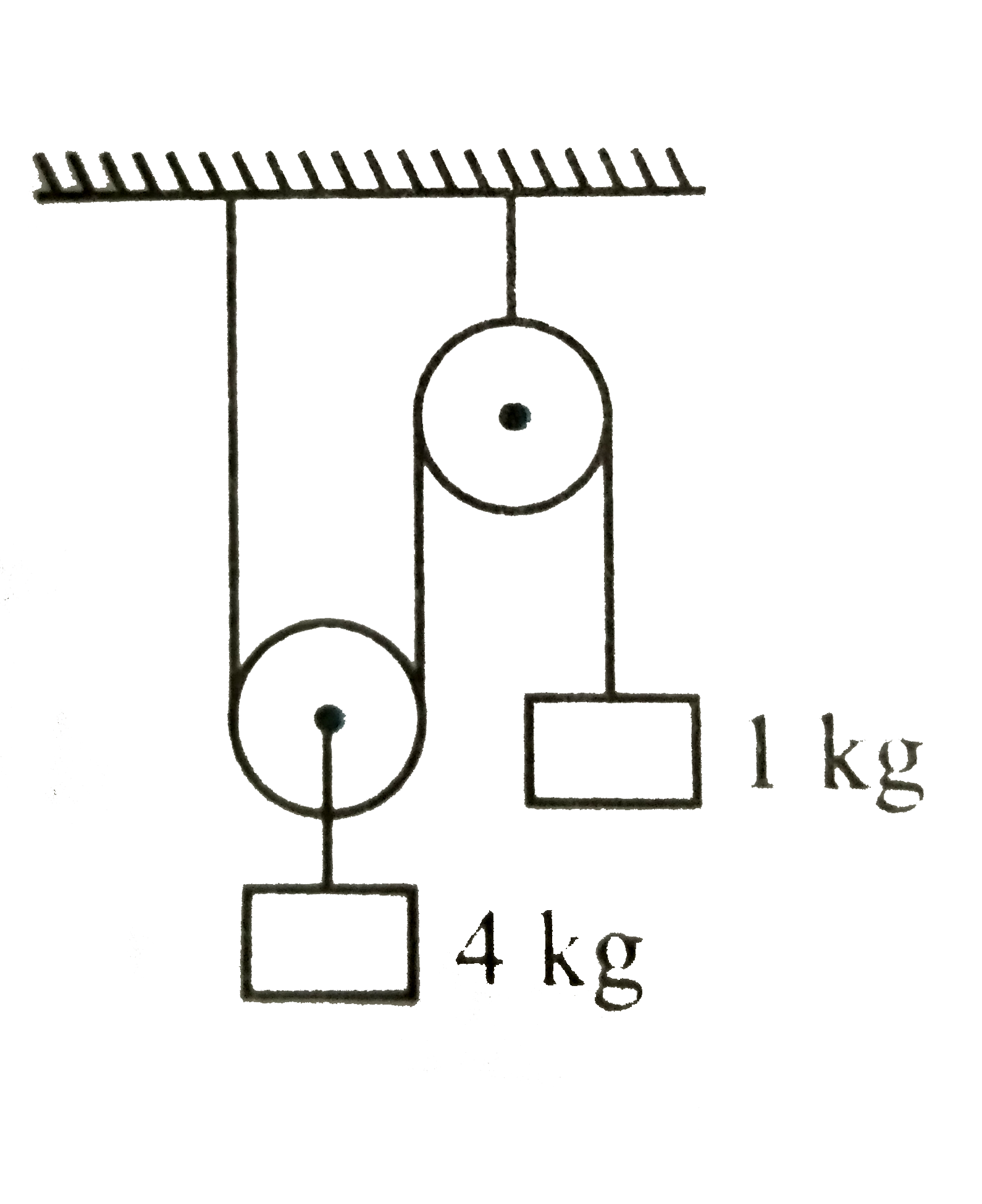
View SolutionIn the system shown in the figure, the acceleration of 1 kg mass is
View SolutionTwo Block A and B of masses 10kg and 6kg respectively are connected through pulley as shown in figure. Find acceleration of block A.
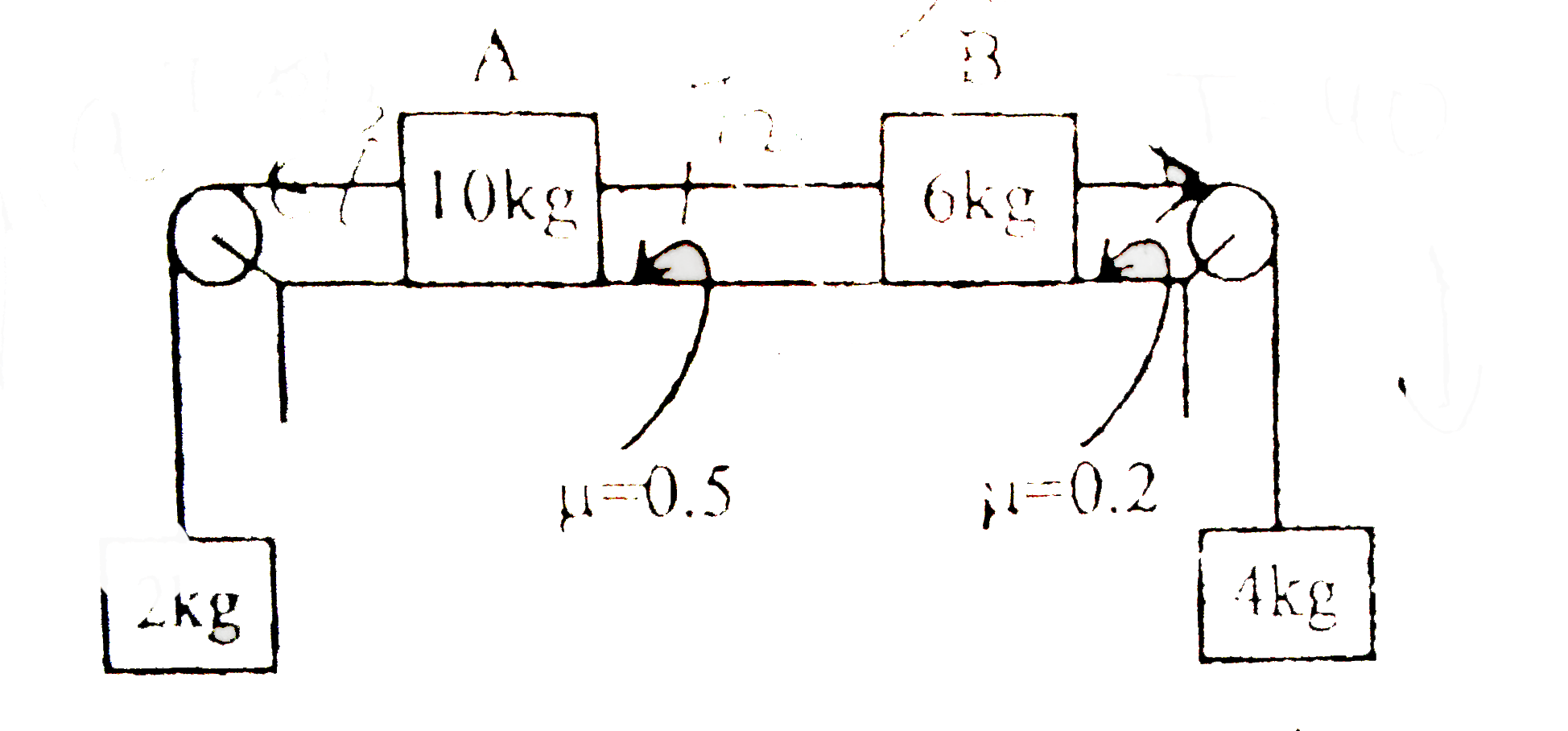
View Solution