A homogeneous rod of length L is acted upon by two forces F1andF2 applied to its ends and directed opposite to each other. With what force F will the rod be stretched at the cross section at a distance l from the end where F1 is applied?
To solve the problem, we need to determine the force F that will stretch the rod at a cross-section located at a distance l from the end where the force F1 is applied. We will follow these steps:
Step 1: Understand the forces acting on the rod
We have a homogeneous rod of length L with two forces F1 and F2 applied at its ends, directed opposite to each other. We assume F2>F1.
Step 2: Define the mass per unit length
Let the mass per unit length of the rod be λ (in kg/m). The total mass of the rod can be expressed as:
Mass of the rod=λ⋅L
Step 3: Write the equation of motion for the entire rod
The net force acting on the rod is given by:
Fnet=F2−F1
According to Newton's second law, this net force is equal to the mass of the rod multiplied by its acceleration A0:
F2−F1=λ⋅L⋅A0(Equation 1)
Step 4: Analyze the section of the rod
Now, consider a section of the rod from the end where F1 is applied to a distance l. The forces acting on this section are F1 at one end and an unknown force F at the other end. The acceleration of this section is also A0.
Step 5: Write the equation of motion for the section of the rod
The net force acting on this section can be expressed as:
F−F1=λ⋅l⋅A0(Equation 2)
Step 6: Relate the two equations
We can now relate Equation 1 and Equation 2. From Equation 1, we have:
A0=F2−F1λ⋅L
Substituting this expression for A0 into Equation 2 gives:
F−F1=λ⋅l⋅(F2−F1λ⋅L)
This simplifies to:
F−F1=lL(F2−F1)
Step 7: Solve for the force F
Rearranging the above equation to solve for F:
F=F1+lL(F2−F1)
This is the expression for the force F that will stretch the rod at the cross-section at a distance l from the end where F1 is applied.
Final Answer
F=F1+lL(F2−F1)
---
We have a homogeneous rod of length L with two forces F1 and F2 applied at its ends, directed opposite to each other. We assume F2>F1.
Let the mass per unit length of the rod be λ (in kg/m). The total mass of the rod can be expressed as:
Mass of the rod=λ⋅L
The net force acting on the rod is given by:
Fnet=F2−F1
According to Newton's second law, this net force is equal to the mass of the rod multiplied by its acceleration A0:
F2−F1=λ⋅L⋅A0(Equation 1)
Now, consider a section of the rod from the end where F1 is applied to a distance l. The forces acting on this section are F1 at one end and an unknown force F at the other end. The acceleration of this section is also A0.
The net force acting on this section can be expressed as:
F−F1=λ⋅l⋅A0(Equation 2)
We can now relate Equation 1 and Equation 2. From Equation 1, we have:
A0=F2−F1λ⋅L
Substituting this expression for A0 into Equation 2 gives:
F−F1=λ⋅l⋅(F2−F1λ⋅L)
This simplifies to:
F−F1=lL(F2−F1)
Rearranging the above equation to solve for F:
F=F1+lL(F2−F1)
This is the expression for the force F that will stretch the rod at the cross-section at a distance l from the end where F1 is applied.
F=F1+lL(F2−F1)
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.3
Explore 19 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.4
Explore 13 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.1
Explore 11 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
A uniform rope of length L is pulled by a constant force F. What is the tension in the rope at a distance l from the end where it is applied?
View SolutionA uniform rope of length L is pulled by a constant force F. What is the tension in the ropww at a distance l from the end where it is applied?
View Solution
Knowledge Check
Two forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
A√F21−F22B√F21+F22C√(F1+F2)DF1+F2Two forces F1 and F2 are acting on a rod abc as shown in figure.
 Aif F1=F2 then τa=τb=τc ( for both forces)Bif F1=F2 then τa=τc≠τb ( for both forces)Cif F1≠F2 then τa≠τb≠τc ( for both forces)Dif F1≠F2 then τa=τc≠τb ( for both forces)
Aif F1=F2 then τa=τb=τc ( for both forces)Bif F1=F2 then τa=τc≠τb ( for both forces)Cif F1≠F2 then τa≠τb≠τc ( for both forces)Dif F1≠F2 then τa=τc≠τb ( for both forces)A body is acted upon by two forces of manitudes F1=√2NandF2=3N which are inclined at 45∘ to each other. There magnitude of resultant force acting on the body is
A17 NB11 NC√17ND√11N
A uniform rope of length of length L is pulled by a force F on a smooth surface. Find tension in the rope at a distance x from the end where force is applied.
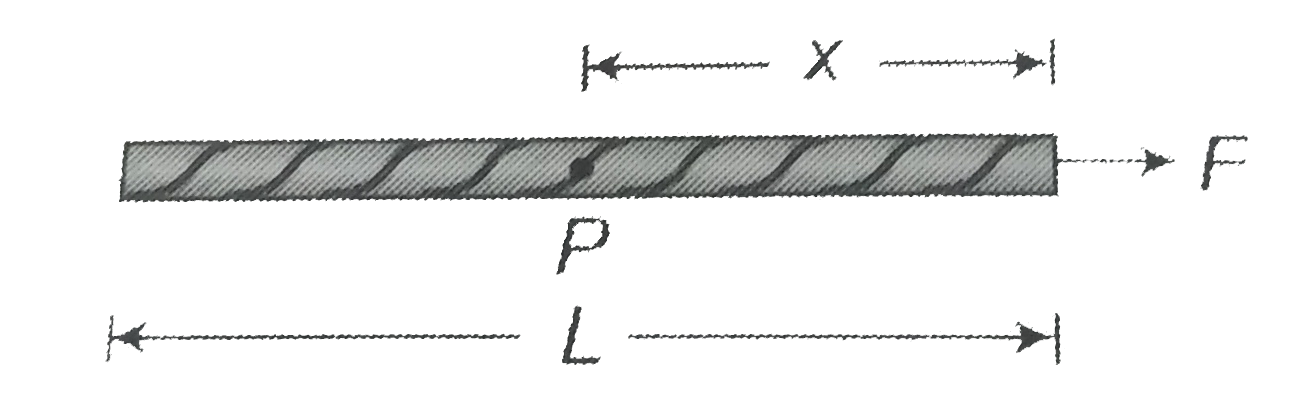
View SolutionA uniform rope of mass M and length L, on which a force F is applied at one end, then find stress in the ropw at a distance x form the end where force is applied?
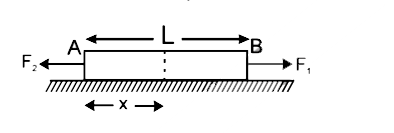
View SolutionTwo forces F1 and F2(F2>F1) are applied at the free ends of uniform rod kept on a horizontal frictionless surface. Find tension in rod at a distance x from end ‘A’,
View SolutionA uniform rod of mass m and length is acted upon by the forces F1 and F2 Find that:
a. linear-and angular acceleration of the rod.
b. value of x for which the point P does not accelerate.

View SolutionA rod of length L and mass M is acted on by two unequal forces F1 and F2(<F)as shown in the figure.
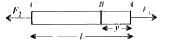
The tension in the rod at a distance y from the end A is given by
View Solution

