A small cubical block is placed on a triangular block M so that they touch each other along a smooth inclined contact plane as shown in fig. The inclined surface makes an angle θ with the horizontal. A force F is to be appled on the block m in horizontal direction so that the two bodies move without slipping against each other assuming the floor to be smooth also. determine the
(a) normal force with which m and M press against each other.
(b) magnitude of external force F. Express your answer in terms of m, M,θ,and g.

When there is no sliding at any contact surface, we may take complete system as a single body.
Considering motion of the system
From FBD of m
F=(M+m)a …(i)
Ncosθ=mg …(ii)
and F−Nsinθ=ma …(iii)
From eq. (ii)N=mgcosθ
Solving Eqs, (i), (ii) and (iii) we get
F=mgM(m+M)tanθ.

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.3
Explore 19 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.4
Explore 13 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Exercise 6.1
Explore 11 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
Similar Questions
A small cubical block is placed on a triangular block M so that ,they touch each other along a smooth inclined contact plane as shown. The, inclined surface makes an angle θ With the horizontal. A hqrizontal force F is to be applied on the block mi so that the two bodies move without slipping against each other. Assuming the floor to be smooth also, determine the

(a) normal force with which m and M press against each other and
(b) the magnitude of external force F. Express your answer in terms of m, M, θ and g.
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View Solution
Knowledge Check
A block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
AmgBmgcosθCmgcosθDmgtanθ
A block is placed on a smooth wedge of inclination angle θ with the horizontal. What minimum acceleration should be given to the wedge in the horizontal direction so that the block starts moving up along the incline?A>gcotθB>>anθC>gsinθD>gcosθA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1Dμmgθ
A block of mas m is placed on a triangular block of mas m, which in tunis placed on a horizontal surface as shown in figure. Assuming frictionless surfaces find the velocity of the triangular block when the smaller block reaches the bottom end.
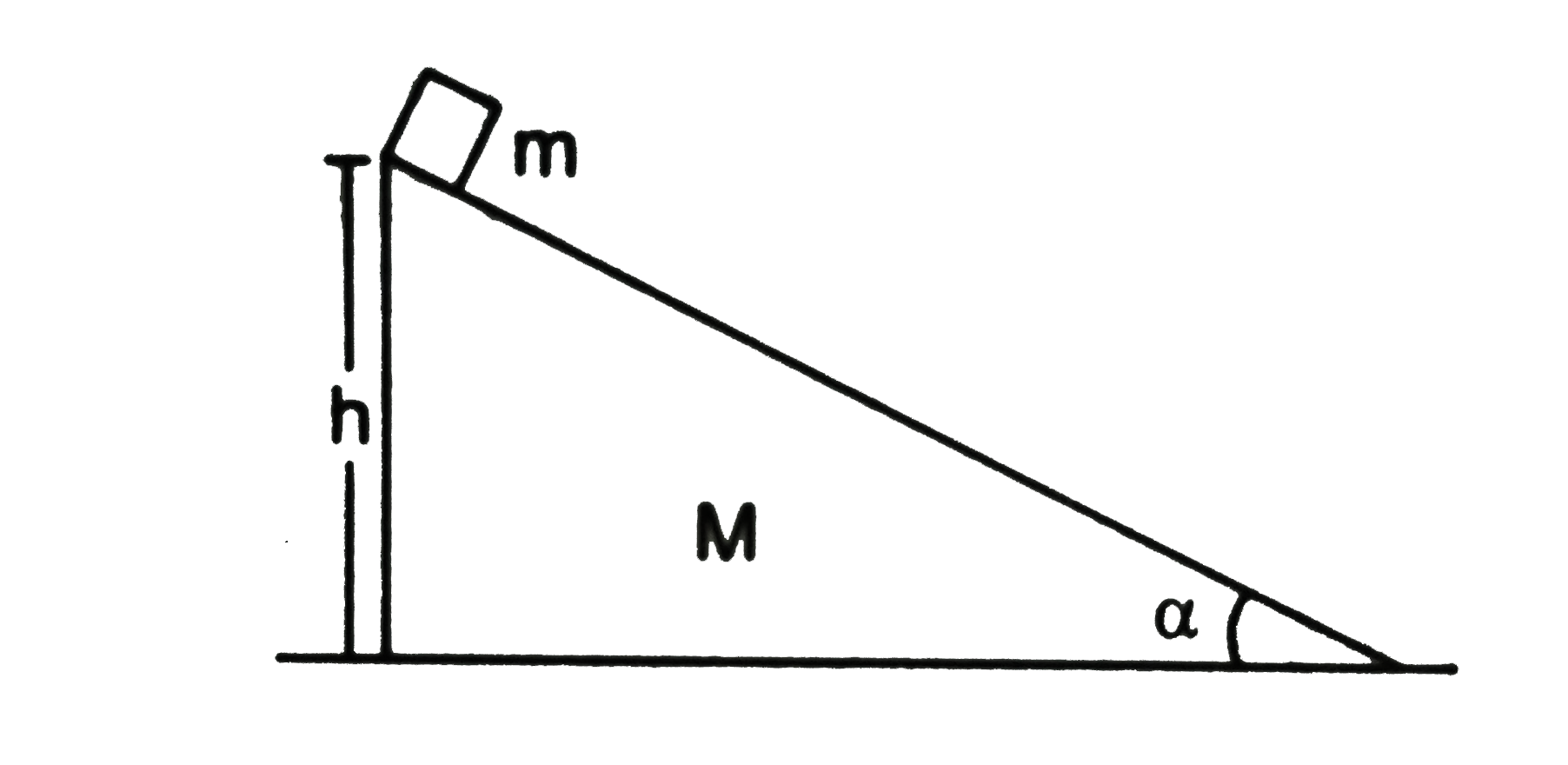
View SolutionA bar of mass m is placed on a triangular block of mass M as shown in figure The friction coefficient between the two surface is μ and ground is smooth find the minimum and maximum horizontal force F required to be applied on block so that the bar will not slip on the inclined surface of block

View SolutionFind the magnitude of the horizontal force F required to keep the block of mass m stationary on the smooth inclined plane as shown in the figure.

View SolutionA block is at rest on an inclined plane making an angle α with the horizontal. As the angle of the incline is increased the block start slipping when the angle of inclination becomes θ then coefficient of friction is equal to
View SolutionStatement I: A block of mass m is placed on a smooth inclined plane of inclinaton θ with the horizontal. The force exerted by the plane on the block has a magnitude mgcosθ.
Statement II: Normal reaction always acts perpendicular to the contact surface.
View Solution

