Two particles, each of mass m, are connected by a light string of length 2L as shown in A continuous force F is applied at the mid point of the string (x=0) at right angles to the initial position of the string. Show that acceleration of m in the direction at right angles to F is given by
ax=F2mx√L2−x2
where x is the perpendicular distance of one of the particles from the line of action of F. Discuss the situation when x=L
Let the mid point of the string O be displaced by y downwards along y- axis, so that at a given instant each string makes an angle θ with the y- axis as shown in
For motion of point C,
F−2Tcosθ=0×ay i.e., T=F/(2cosθ)....(i)
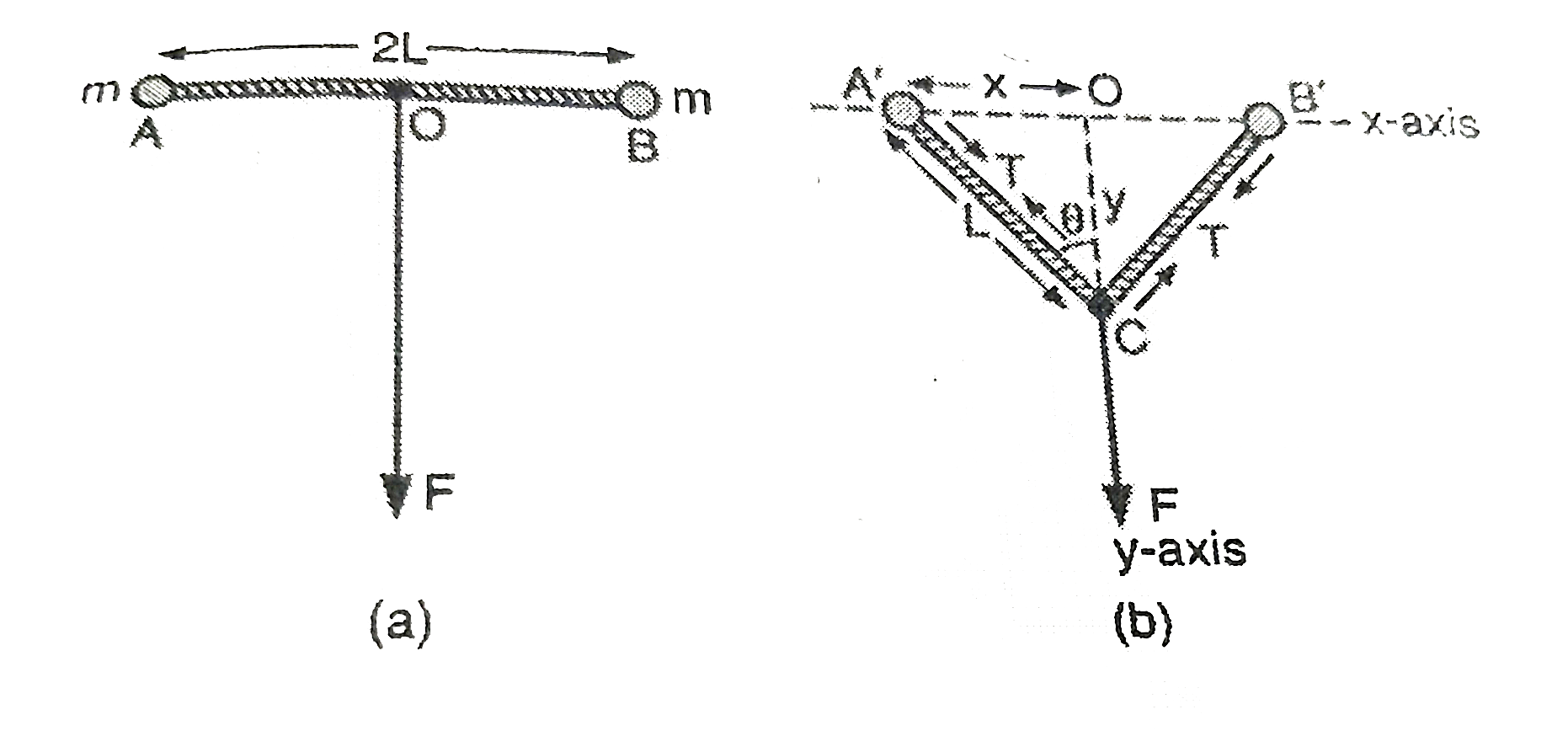
Now consider the motion of mass m at A towards B or vice-versa. Then as component of T in the direction of motion will be Tcos(90∘−θ)=Tsinthetha , so if ax is the acceleration of m along x-axis, then from F=ma
Tsinθ=maxorax=Tsinθ/m ....(ii)
Substituting the value of T from Eqn (i) in (ii)
ax=F2cosθ×sinθm=F2mtanθ=F2mx√L2−x2
This is the required result From this, it is clear that if x=L,ax=∞ i.e, this situation cannot be realised in pratice as when F is applied, the mid point of string will be depressed in the y direction and so x cannot remain equal to L.
Note: (i) Acceleration of particle in the direction of force will be,
ay=Tcosθm=F2m=constant
(ii) As particles move towards each other x or θ will decrease and so also the acceleration ax and for x=0,(θ=0∘)ax=0
Topper's Solved these Questions
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Problem for practice
Explore 30 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Objective Questions
Explore 134 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- BASIC MATHEMATICSBook:GRB PUBLICATIONChapter:BASIC MATHEMATICSExercise:Problems For Practice
Explore 35 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
Similar Questions
Two particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x
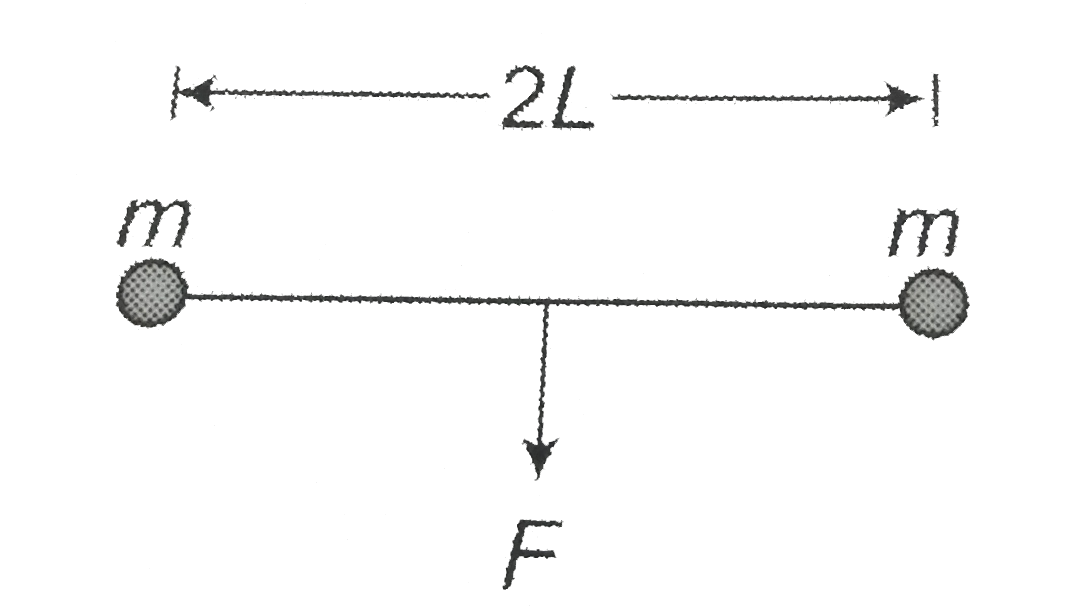
View SolutionTwo particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x

View Solution
Knowledge Check
Two small sphere each of mass m connected by a string of length 2l are kept on a smooth horizontal surface. A vertical force F is applied at the middle of the string. What is maximum value of F for which the sphere do not lose contact with the surface?
 A2mgBmgC3mg2D4mg
A2mgBmgC3mg2D4mgAn object of mass 10kg is connected to the lower end of a massless string of length 4m hanging from the ceiling. If a force F is applied horizontally at the mid-point of the string, the top half of the string makes an angle of 45∘ with the vertical , then the magnitude of F is
A75NB90NC100ND70 NAn object of mass m is tied to a string of length l and a variable force F is applied on it which brings the string gradually at angle θ with the vertical. Find the work done by the force F.
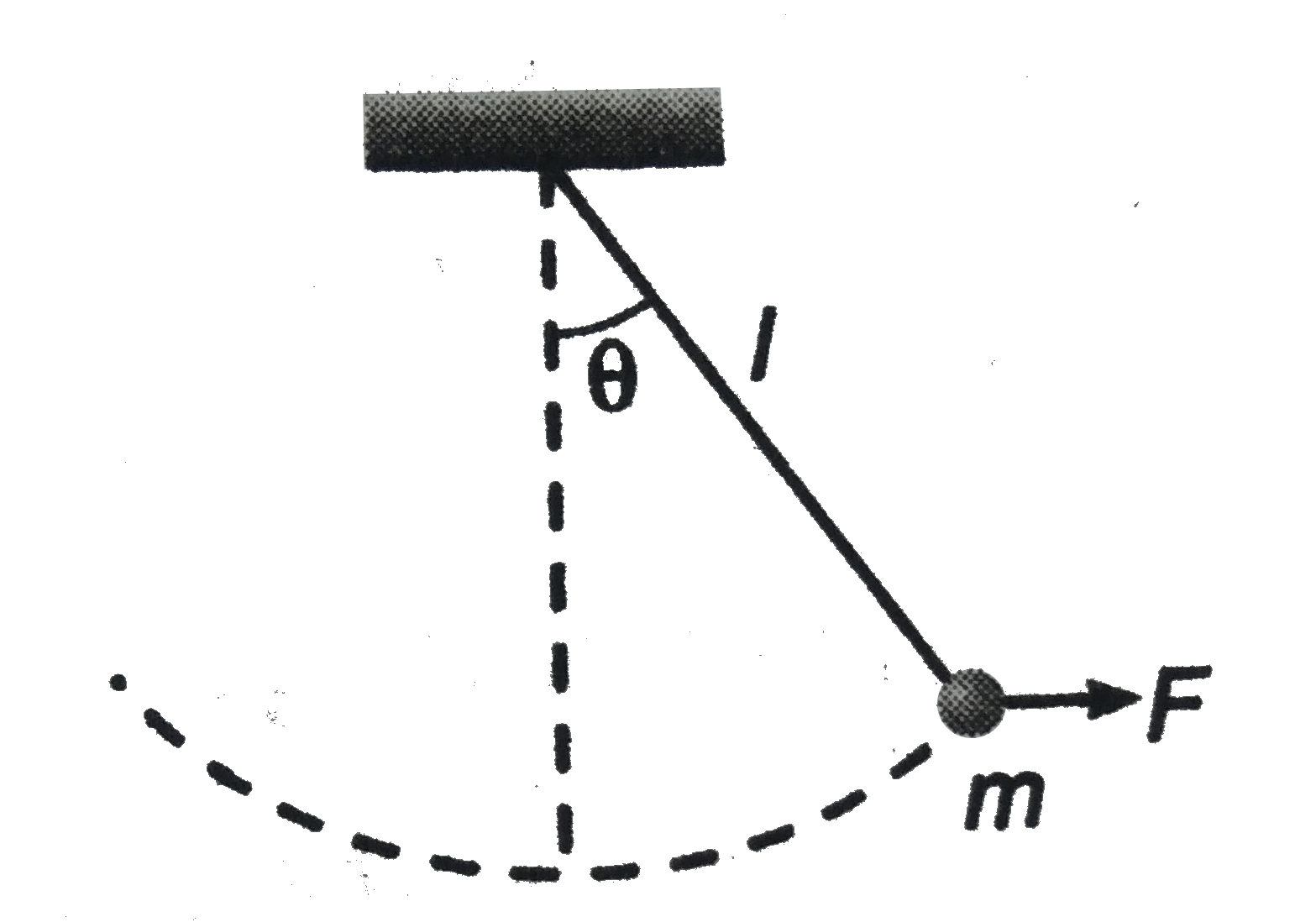 . Amgl(1+cosθ)Bmgl(1−cosθ)Cmgl(1−cosθ)Dmgl(1+cosθ)
. Amgl(1+cosθ)Bmgl(1−cosθ)Cmgl(1−cosθ)Dmgl(1+cosθ)
Two particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View SolutionTwo masses M and m are connected by a weightless string. They are pulled by a force F on a frictionless horizontal surface. The tension in the string will be
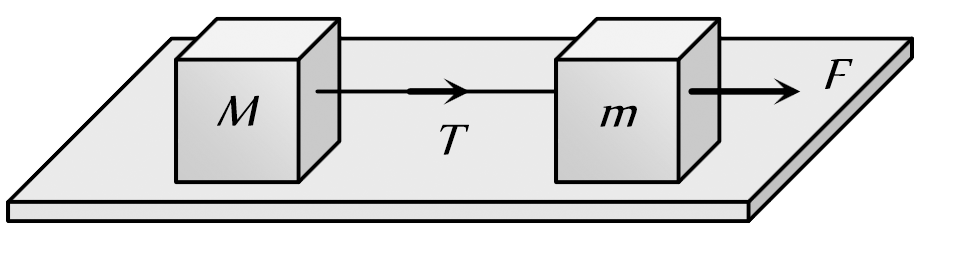
View SolutionTwo particles of masses m1 and m2 are connected with a rigid rod of length l. If a force F acts perpendicular to the rod then (a1&a2 are instantaneous of m1&m2)

View Solution

