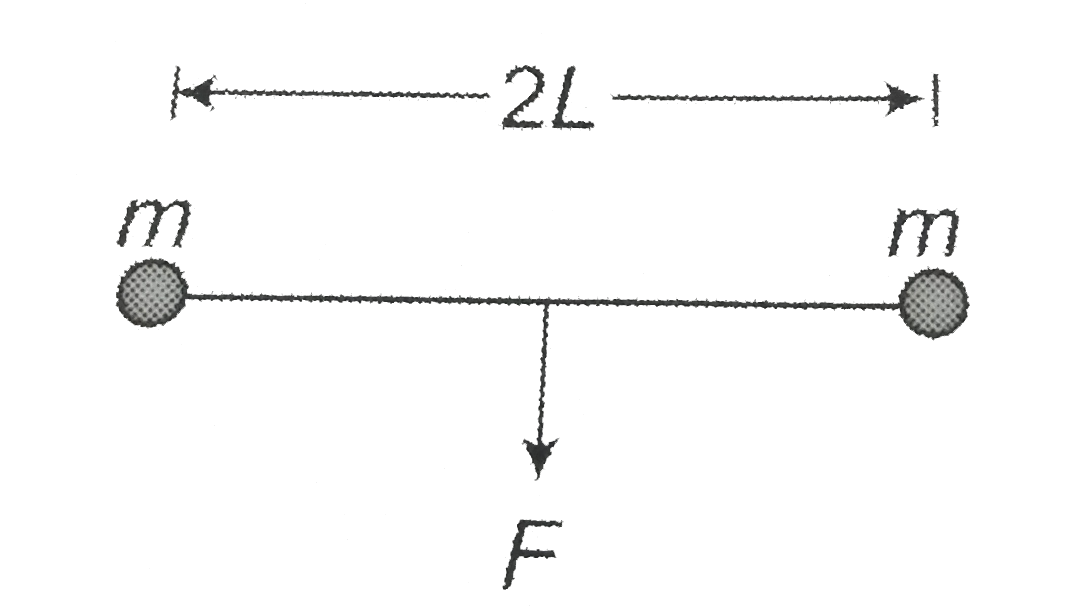
Two particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x
When the separation between particles is 2x
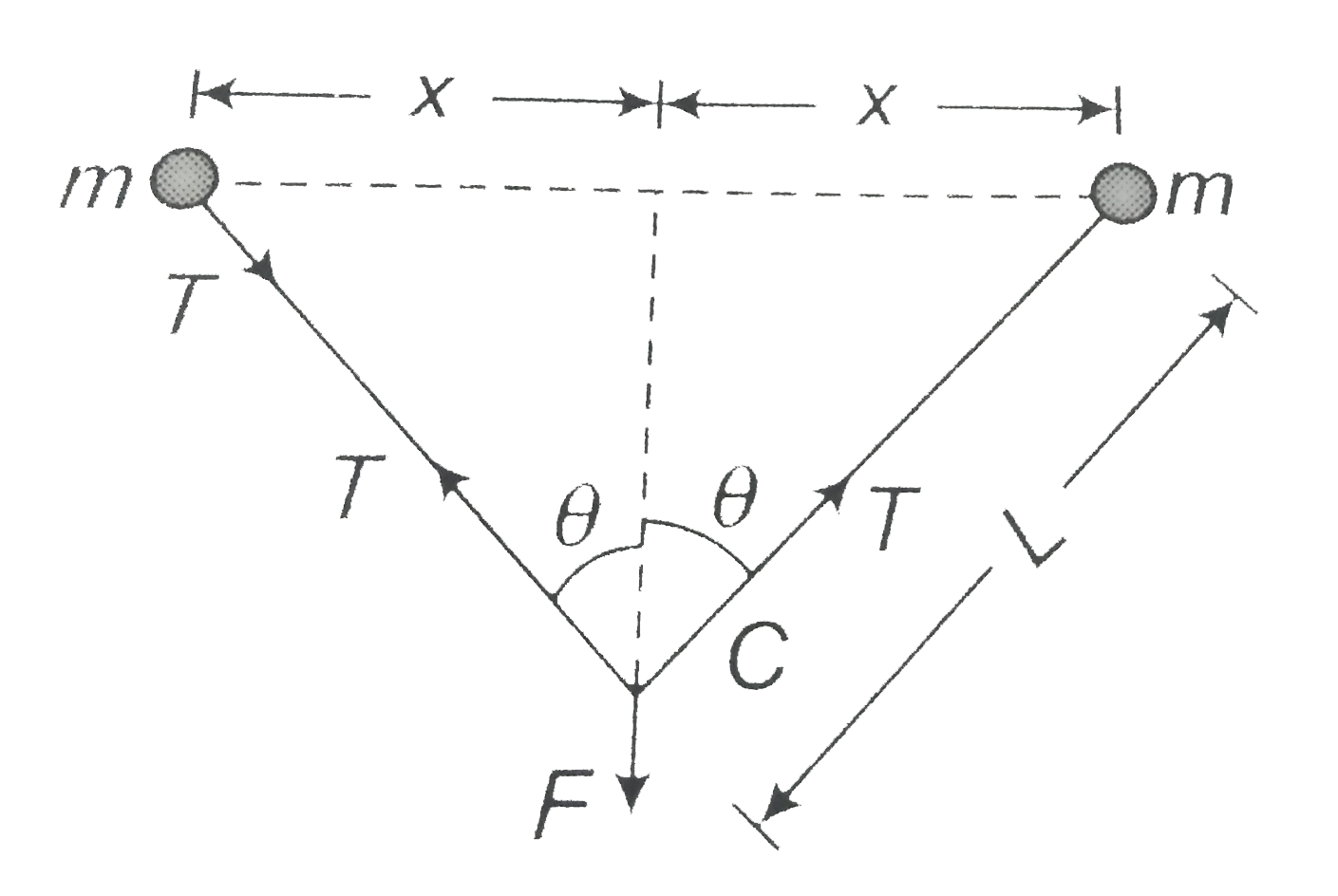 Point C:
Point C:
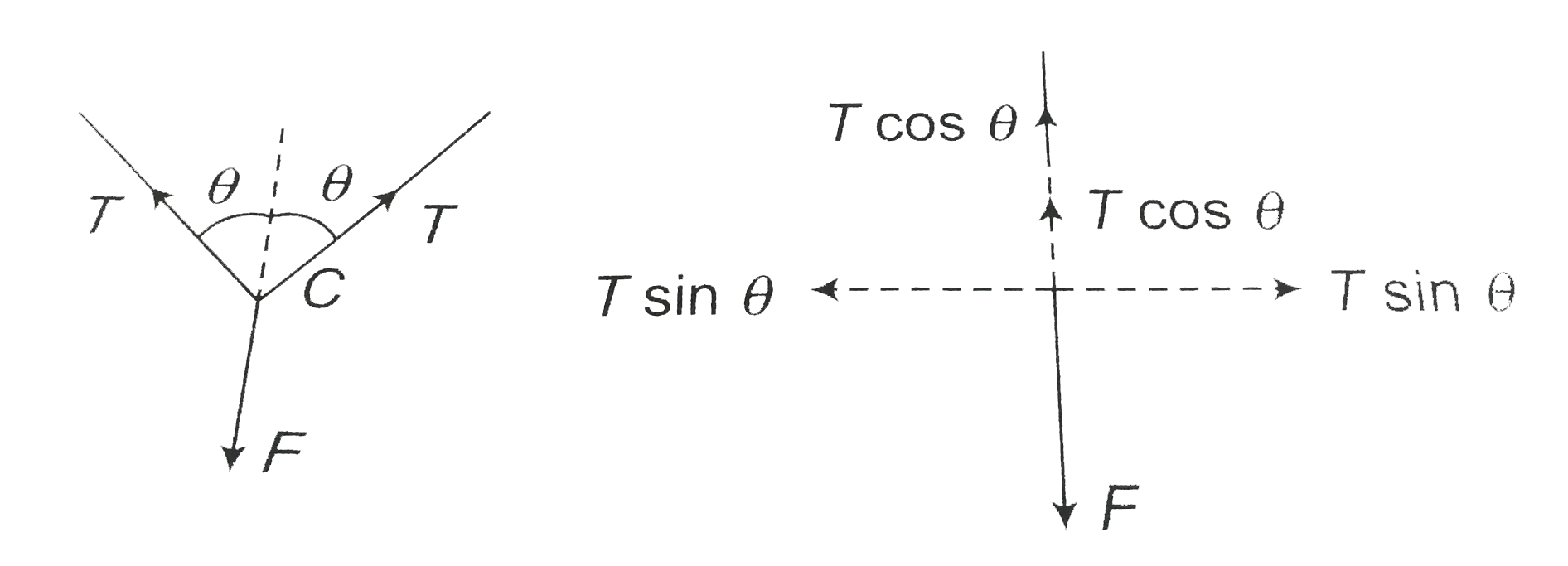
2Tcosθ=F
T=F2cosθ
Particle:
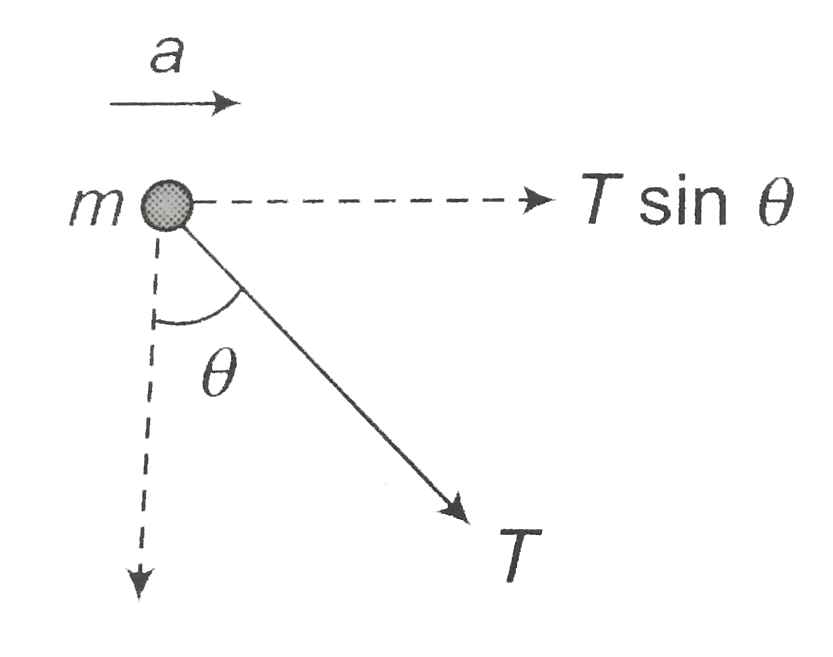
Tsinθ=ma
F2cosθsinθ=ma
Acceleration of particle
a=F2mtanθ=F2m×x√L2−x2
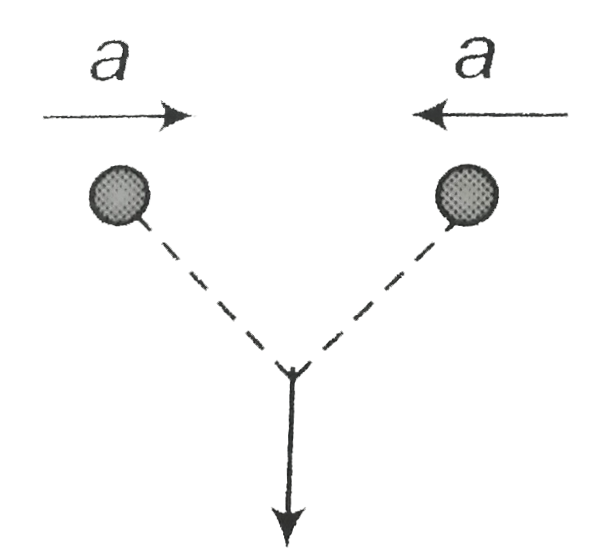 Acceleration of approach h=a+a=2a
Acceleration of approach h=a+a=2a
=Fm×x√L2−x2
Topper's Solved these Questions
Similar Questions
Two particles, each of mass m, are connected by a light string of length 2L as shown in A continuous force F is applied at the mid point of the string (x=0) at right angles to the initial position of the string. Show that acceleration of m in the direction at right angles to F is given by
ax=F2mx√L2−x2
where x is the perpendicular distance of one of the particles from the line of action of F. Discuss the situation when x=L
View SolutionTwo particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x

View Solution
Knowledge Check
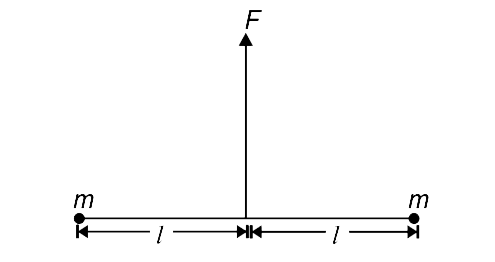
An object of mass 10kg is connected to the lower end of a massless string of length 4m hanging from the ceiling. If a force F is applied horizontally at the mid-point of the string, the top half of the string makes an angle of 45∘ with the vertical , then the magnitude of F is
A75NB90NC100ND70 NA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are
 AmgandTBmg,T,mv2rdirected in wardsCmg,T,mv2rdirected outewardsDmv2ronly
AmgandTBmg,T,mv2rdirected in wardsCmg,T,mv2rdirected outewardsDmv2ronly
Two particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

View SolutionTwo small balls, each of mass m are placed on a smooth table, connected with a light string of length 2l, as shown in the figure. The midpoint of the string is pulled along y direction by applying a constant force F. Find the relative speed of the two particles when they are about to collide. If the two masses collide and stick to each other, how much kinetic energy is lost.
View SolutionA constant force F=m_2g/sisappliedontheblockofmassm_1asshown∈figure.Thestr∈gandthep≤––––yarelightandthesurfaceofthetab≤issm∞th.F∈dtheae≤rationofm_1
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View SolutionA uniform rod of mass m and length 2L on a smooth horizontal surface. A particle of mass m is connected to a string of length L whose other end is connected to the end ‘A’ of the rod. Initially the string is held taut perpendicular to the rod and the particle is given a velocity v0 parallel to the initial position of the rod.
(a) Calculate the acceleration of the centre of the rod immediately after the particle is projected.
(b) The particle strikes the centre of the rod and sticks to it. Calculate the angular speed of the rod after this.

View SolutionTwo point masses, each of mass 'm' are connected to the end of spring. If force F is applied on one of the mass, then find the acceleration of this mass if the acceleration of other mass is a ?

View Solution