A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
m2gm1+m2
m1gm1+m2
g
m2gm1
The correct Answer is:A
To find the acceleration of the system consisting of two blocks connected by a string over a frictionless pulley, we can follow these steps:
Step 1: Identify the Forces Acting on Each Block
- For block m1 on the table, the only force acting on it horizontally is the tension T in the string.
- For block m2 hanging vertically, the forces acting on it are its weight m2g (downward) and the tension T (upward).
Step 2: Write the Equations of Motion
- For block m1 (on the table):
T=m1a(1)
- For block m2 (hanging):
m2g−T=m2a(2)
Step 3: Solve the Equations Simultaneously
- From equation (1), we can express T in terms of a:
T=m1a
- Substitute this expression for T into equation (2):
m2g−m1a=m2a
Step 4: Rearrange the Equation
- Rearranging the equation gives:
m2g=m1a+m2a
- Factor out a from the right side:
m2g=(m1+m2)a
Step 5: Solve for Acceleration a
- Now, we can solve for a:
a=m2gm1+m2
Final Result
Thus, the acceleration of the system is:
a=m2gm1+m2
---
- For block m1 on the table, the only force acting on it horizontally is the tension T in the string.
- For block m2 hanging vertically, the forces acting on it are its weight m2g (downward) and the tension T (upward).
- For block m1 (on the table):
T=m1a(1)
- For block m2 (hanging):
m2g−T=m2a(2)
- From equation (1), we can express T in terms of a:
T=m1a
- Substitute this expression for T into equation (2):
m2g−m1a=m2a
- Rearranging the equation gives:
m2g=m1a+m2a
- Factor out a from the right side:
m2g=(m1+m2)a
- Now, we can solve for a:
a=m2gm1+m2
Thus, the acceleration of the system is:
a=m2gm1+m2
Topper's Solved these Questions
Similar Questions
A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View SolutionA block of mass m1 rests on a rough horizontal plane with which its coefficient of friction is μ. A light string attached to this block passes over a light frictionless pulley and carries another block of mass m2 as shown in figure-2.213. When the system is just about to move, find the value of μ in terms of m1m2 and α. Also find the tension in the string.
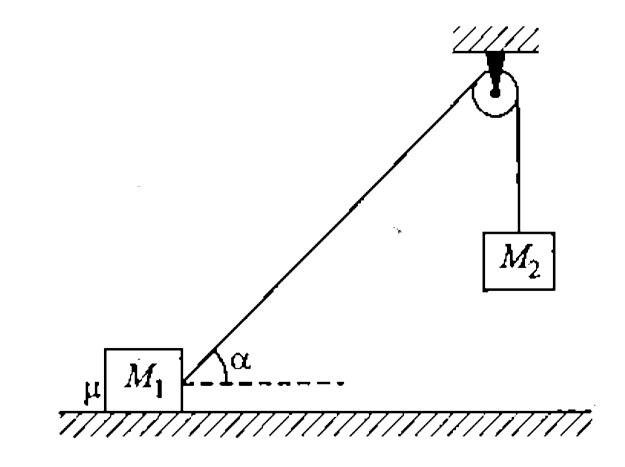
View Solution
Knowledge Check
A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pully at the edge of the table and from its other end another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table is H. When the block A is sliding on the table, the tension in the string is
Am1m2(1+μk)g(m1+m2)Bm1m2(1−μk)g(m1)+m2C(m2+μkm1)g(m1+m2)D(m2−μkm1)g(m1+m2)A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of knetic friction between the block and table is μk . When the block A is sliding on the table, the tension in the string is.
A(m2+μkm1)gm1+m2B(m2−μkm1)gm1+m2Cm1m2(1+μk)g(m1+m2)Dm1m2(1−μk)g(m1+m2)A block of mass m1 rests on a rough horizontal plane with coefficient of friction as μ. A light strin attached to this block passes over a light frictionless pulley and carries another block of mass m2 as shown in figure. If the system is just about to move, then find the value of μ.
 Am2cosθm1−m2sinαBm1sinαm1−m2sinαCm2cosαm1+μ2sinαDm1sinαm1+m2sinα
Am2cosθm1−m2sinαBm1sinαm1−m2sinαCm2cosαm1+μ2sinαDm1sinαm1+m2sinα
A block A of mass 5√4m rests on a rough horizontal plane relative to which its coefficient of friction is μA light string attached to this block passes over a light frictionless pulley and another block B of mass m hangs from it. It is observed that the block A just slips when the string makes an angle of 60∘ with the horizontal .
Find the coefficient of static friction between the block A and the plane. If the same force acting through the sting is applied to the block A in the horizontal direction, find the acceleration of the block A.
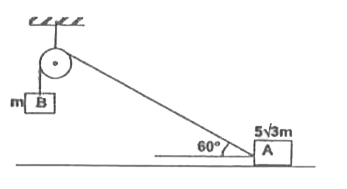
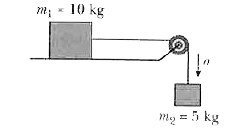
View SolutionA body of mass 10 kg is placed on the horizontal smooth table (see given figure). A string is tied with it which passes over a frictionless pulley. The other end of the string is tied with a body of mass 5 kg. When the bodies move, the acceleration produced in them, is
View SolutionA block A of mass 7 kg is placed on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 3 kg at the other end. The acceleration of the system is (given g=10ms−2)

View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is

View SolutionThe block of mass m is at rest. Find the tension in the string A .

View Solution