A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
We can draw free body diagrams for each individual part of the system. When the nail fixed on the table gets removed, the system of two bodies moves with an acceleration (a), as shown in figure
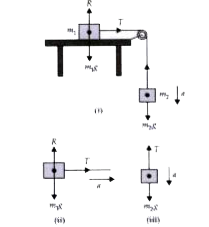
Equations of motion can be written as
m2g−T=m2a
T=m1a......(ii)
R=m1g.....(iii)
Adding (i) and (ii) we get
m2g=(m2+m1)aora=m2g(m2+m1)
Putting the given values , we get
a=8×10(8+12)=4ms−2
Topper's Solved these Questions
- FORCE AND LAWS OF MOTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - OLYMPIAD /HOTS CORNER
20 Videos
- FORCE AND LAWS OF MOTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - EXERCISE (LONG ANSWER TYPE)
9 Videos
- FOOTSTEPS TOWARDS NEETBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS NEETEXERCISE - Multiple Choice Question
45 Videos
- GRAVITATION BOOK - MTG IIT JEE FOUNDATIONCHAPTER - GRAVITATION EXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View SolutionA block of mass m1 rests on a rough horizontal plane with which its coefficient of friction is μ. A light string attached to this block passes over a light frictionless pulley and carries another block of mass m2 as shown in figure-2.213. When the system is just about to move, find the value of μ in terms of m1m2 and α. Also find the tension in the string.
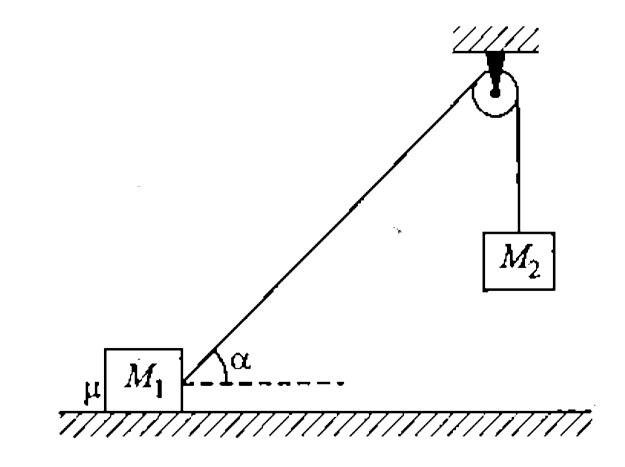
View Solution
Knowledge Check
A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pully at the edge of the table and from its other end another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table is H. When the block A is sliding on the table, the tension in the string is
Am1m2(1+μk)g(m1+m2)Bm1m2(1−μk)g(m1)+m2C(m2+μkm1)g(m1+m2)D(m2−μkm1)g(m1+m2)A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block B of mass m2 is suspended. The coefficient of knetic friction between the block and table is μk . When the block A is sliding on the table, the tension in the string is.
A(m2+μkm1)gm1+m2B(m2−μkm1)gm1+m2Cm1m2(1+μk)g(m1+m2)Dm1m2(1−μk)g(m1+m2)A block of mass m1 rests on a rough horizontal plane with coefficient of friction as μ. A light strin attached to this block passes over a light frictionless pulley and carries another block of mass m2 as shown in figure. If the system is just about to move, then find the value of μ.
 Am2cosθm1−m2sinαBm1sinαm1−m2sinαCm2cosαm1+μ2sinαDm1sinαm1+m2sinα
Am2cosθm1−m2sinαBm1sinαm1−m2sinαCm2cosαm1+μ2sinαDm1sinαm1+m2sinα
A block A of mass 5√4m rests on a rough horizontal plane relative to which its coefficient of friction is μA light string attached to this block passes over a light frictionless pulley and another block B of mass m hangs from it. It is observed that the block A just slips when the string makes an angle of 60∘ with the horizontal .
Find the coefficient of static friction between the block A and the plane. If the same force acting through the sting is applied to the block A in the horizontal direction, find the acceleration of the block A.
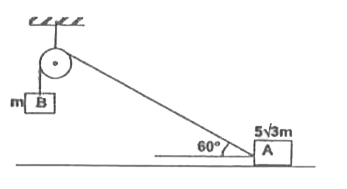
View SolutionA body of mass 10 kg is placed on the horizontal smooth table (see given figure). A string is tied with it which passes over a frictionless pulley. The other end of the string is tied with a body of mass 5 kg. When the bodies move, the acceleration produced in them, is
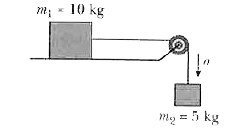
View SolutionA block A of mass 7 kg is placed on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 3 kg at the other end. The acceleration of the system is (given g=10ms−2)

View SolutionThe block of mass m is at rest. Find the tension in the string A .

View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is

View Solution
