Question

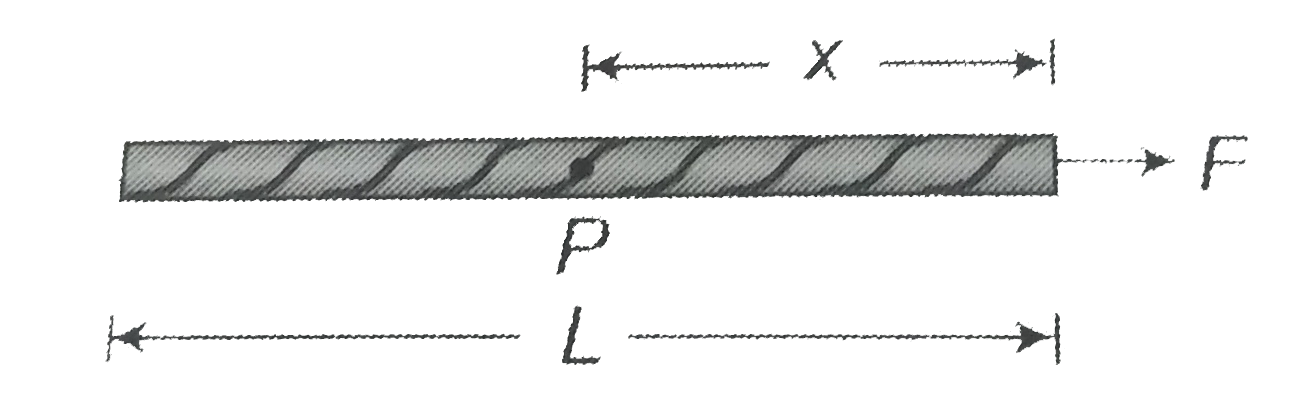
A string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is

Options

A. Zero
B. F should be equal to the weight of A and B
C. F(L-x)/L
D. F(L-x)M

Answer

C

Explanation

To solve the problem of finding the tension in a string of length $$L$$ and mass $$M$$ when a force $$F$$ is applied at one end, we can follow these steps:

1. Understanding the System:
- We have a string of length \( L \) and mass \( M \) lying on a horizontal table.
- A force \( F \) is applied at one end of the string, causing tension throughout the string.

2. Identifying the Distance:
- We need to find the tension at a distance \( x \) from the end where the force is applied.
- The length of the string that is not considered for tension calculation is \( L - x \).

3. Calculating the Mass of the Segment:
- The mass per unit length of the string is given by \( \frac{M}{L} \).
- The mass of the segment of the string from the point where the force is applied to the point \( x \) is:
\( M' = \frac{M}{L} \cdot (L - x) \)

4. Finding the Acceleration:
- The entire string accelerates due to the applied force \( F \).
- The total mass of the string is \( M \), so the acceleration \( a \) of the string can be calculated using Newton's second law:
\( a = \frac{F}{M} \)

5. Applying Newton's Second Law to the Segment:
- The tension \( T \) at distance \( x \) must support the mass \( M' \) of the segment of the string that is being accelerated.
- According to Newton's second law:
\( T = M' \cdot a \)
- Substituting for \( M' \) and \( a \):
\( T = \left(\frac{M}{L} \cdot (L - x)\right) \cdot \left(\frac{F}{M}\right) \)

6. Simplifying the Expression:
- The mass \( M \) cancels out:
\( T = \frac{F \cdot (L - x)}{L} \)

7. Final Result:
- Therefore, the tension in the string at a distance \( x \) from the end where the force is applied is:
\( T = \frac{F \cdot (L - x)}{L} \)