A Body moving radially away from a planet of mas M, when at distance r from planet, explodes in such a way that two of its many fragments move in mutually prependicular circular orbits around the planet what will be
(i). Then velocity in circular orbits?
(ii). Maximum distance between the two fragments before collision and
(iii). Magnitude of their relative velocity just before they collide?
The correct Answer is:(a) √GMr ; (b) r√2; (c ) √2GMr
(i) Centripetal force is provided by gravitational field.
m1v2r=GMmr2⇒v=√GMr
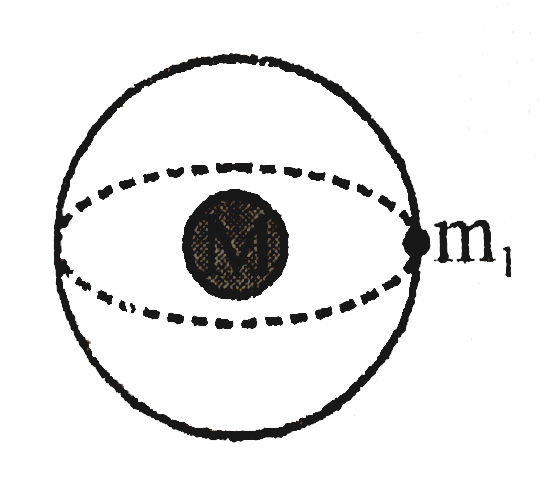
(ii) Maximum distance =√2r
(iii) Relative velocity just before collision
Mag. of relative velocity =√2v=√2GMr
Topper's Solved these Questions
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -4 Section - A
Explore 16 Videos
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -4 Section - B
Explore 6 Videos
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -2 [Matrix Type]
Explore 1 Video
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)
Explore 8 Videos
- HEAT TRANSFERBook:BANSALChapter:HEAT TRANSFERExercise:Exercise
Explore 89 Videos
Similar Questions
A body moving radially away from a planet of mass M, when at distance r from planet, explodes in such a way that two of its many fragments move in mutually perpendicular circular orbits around the planet. What will be
View SolutionIf the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, its areal velocity is :
View Solution
Knowledge Check
A body of mass m is moving in a circular orbit of radius R about a planet of mass M. At some instant, it splits into two equal masses. The first mass moves in a circular orbit of radius R2. And the other mass, in a circular orbit of radius 3R2. The difference between the final and initial total energies is :
A−GMm2RBGMm2RC−GMm6RD+GMm6RTwo satellites X and Y are moving in circular orbits of radii R and 2R respectively, around the same planet. What is the ratio of their critical velocities ?
A√2:1B√3:1C1:1√2D1:2A satellite can be in a geostationary orbit around earth at a distance r from the centrer. If the angular velocity of earth about its axis doubles, a satellite can now be in a geostationary orbit around if its distance from the centre is
Ar2Br2√2Cr(4)1/3Dr(2)1/3
Assuming that a planet goes round the sun in a circular orbit of radius 0.5AU determine the angle of maximum elongation for the planet and its distance from the earth when elongation is measured.
View SolutionA body is moving in a low circular orbit about a planet of mass M and radius R. The radius of the orbit can be taken to be R itself. Then the ratio of the speed of this body in the orbit to the escape velocity from the planet is :
View SolutionA planet of mass m is revolving around the sun in an elliptical orbit. The minimum and maximum distances of the planet from the sun are s1 and s2. Derive the relation between time period of the planet in terms of s1 and s2.
View SolutionA satellite is put in an orbit just above the earth's atmosphere with a velocity √1.5 times the velocity for a circular orbit at the that height. The initial velocity imparted is horizontal. What would be the maximum distance of the satellite from the earth, when it is in the orbit.
View SolutionA planet moving in a circular orbit around the sun at a distance, 4times theaverage distance of the earth from the sun will complete one revolution in
View Solution

