Imagine a frictionless tunnel along a chord of earth having length equal to radius of earth R. Particle is thrown from surface of earth inside it along its length at a velocity $\sqrt{\frac{3 g R}{4}}$ where is acceleration due to gravity on surface of earth. Find the time (in sec) taken by particle to cross the tunnel. Take $g = 10 m / s^{2}, π = 3.14$ and $R = 6400 k m$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $837.33 sec$

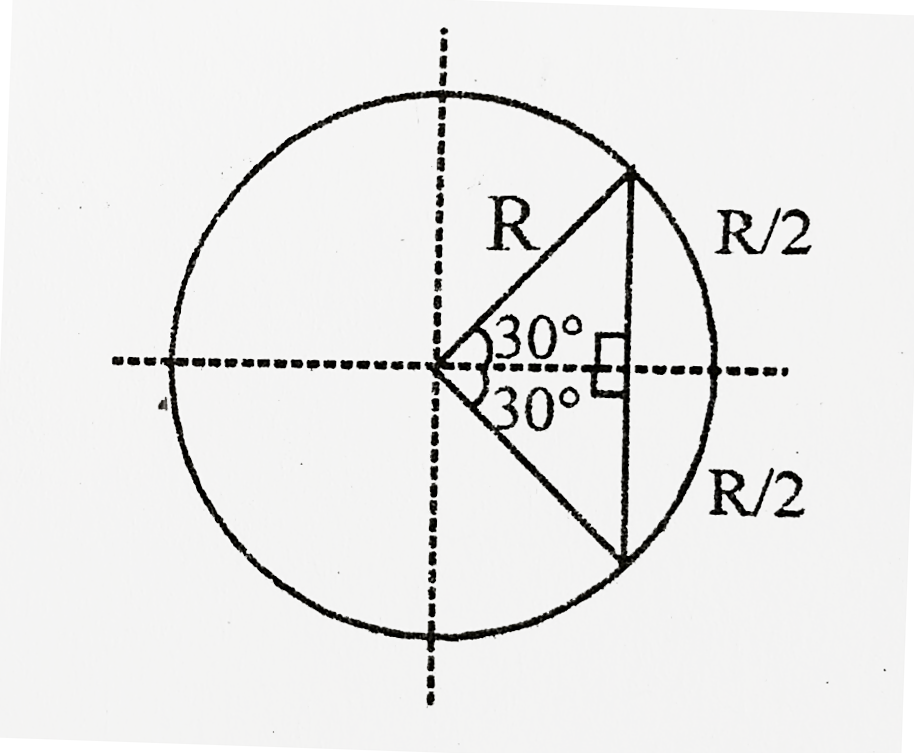
The particle will perform SHM $(w = \sqrt{\frac{G M}{R^{3}}} = \sqrt{\frac{g}{R}})$
$= w \sqrt{A^{2} - \frac{R^{2}}{4}} = \sqrt{\frac{3 g R}{4}}$
$= \sqrt{\frac{g}{R}} \sqrt{A^{2} - \frac{R^{2}}{4}} = \sqrt{\frac{3 g R}{4}}$
$= A^{2} - \frac{R^{2}}{4} = \frac{3}{4} R^{2}$
$A^{2} = R^{2}$
$A = R$
$t = \frac{π}{3 w} = \frac{π}{3} \sqrt{\frac{R}{g}}$
$= \frac{3.14}{3} \times 800 \Rightarrow 837.33 sec$ .

|

Updated on:21/07/2023

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is projected vertically upwards with a velocity $\sqrt{g R}$ , where $R$ denotes the radius of the earth and $g$ the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
A $\frac{R}{2}$
B $R$
C $2 R$
D $\frac{5 R}{4}$
Question 2 - Select One
When a falling meteor is at a distance above the earth's surface 3 times the earth's radius, the acceleration due to gravity at that point is, (where g is acceleration due to gravity on the surface of the earth)
Ag/16
Bg/4
C16 g
Dg/9
Question 3 - Select One
A hole is bored along a diameter of the earth and a particle is dropped into it. If R is the radius of the earth and g is the acceleration due to gravity at the surface of the earth, then the time period of oscillation of the particle is
A $2 π \sqrt{\frac{R}{g}}$
B $2 π \sqrt{\frac{R}{2 g}}$
C $2 π \sqrt{\frac{2 R}{g}}$
Dnone of these

BANSAL-GRAVITATION-EXERCISE -3 [Miscellaneous Exercise]

Home
Ask Doubt
Profile