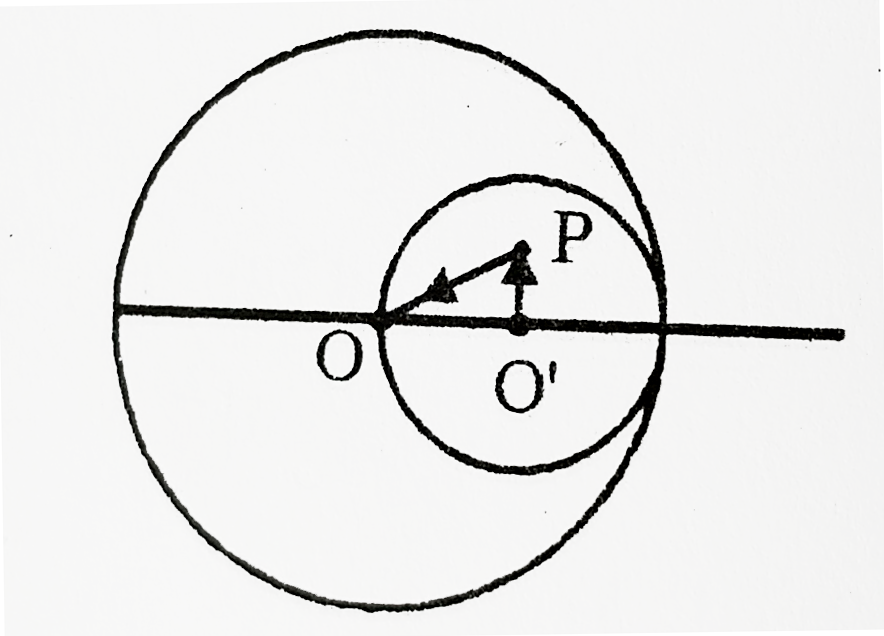
A sphere of radius has its centre at the origin. It has a uniform mass density except that there is a spherical hole of radius whose centre is at as in fig (a) find gravitational field at points on the axis for (ii) Show that the gravitational field inside the hole is uniform, find its magnitude and direction.

The correct Answer is:
From the principal of superpostion field may be consider due to a solid sphere of (Radius R) positive mass and solid sphere of (Radius R/2) having nagative mass.
(i)
(ii) = Field due to sphere (R ) of positive mass + field due to sphere (R/2) of negative mas
Topper's Solved these Questions
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -4 Section - A
Explore 16 Videos
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -4 Section - B
Explore 6 Videos
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -2 [Matrix Type]
Explore 1 Video
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)
Explore 8 Videos
- HEAT TRANSFERBook:BANSALChapter:HEAT TRANSFERExercise:Exercise
Explore 89 Videos
Similar Questions
A current is passing through a cylindrical conductor with a hole (or cavity) inside it. Show that the magnetic field inside the hole is uniform and find its magnitude and direction.
View SolutionInside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength G of the gravitational field inside the cavity.
View Solution
Knowledge Check
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
AE=−23πGρlBE=−43πGρlCE=−43π2GρlDE=−43πGρ2l2A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2Mass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field
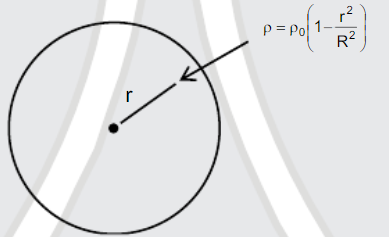 A4π3(Gρ0R)B2π√35(Gρ0R)C8π√527(Gρ0R)D2π√527(Gρ0R)
A4π3(Gρ0R)B2π√35(Gρ0R)C8π√527(Gρ0R)D2π√527(Gρ0R)
A uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.

View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

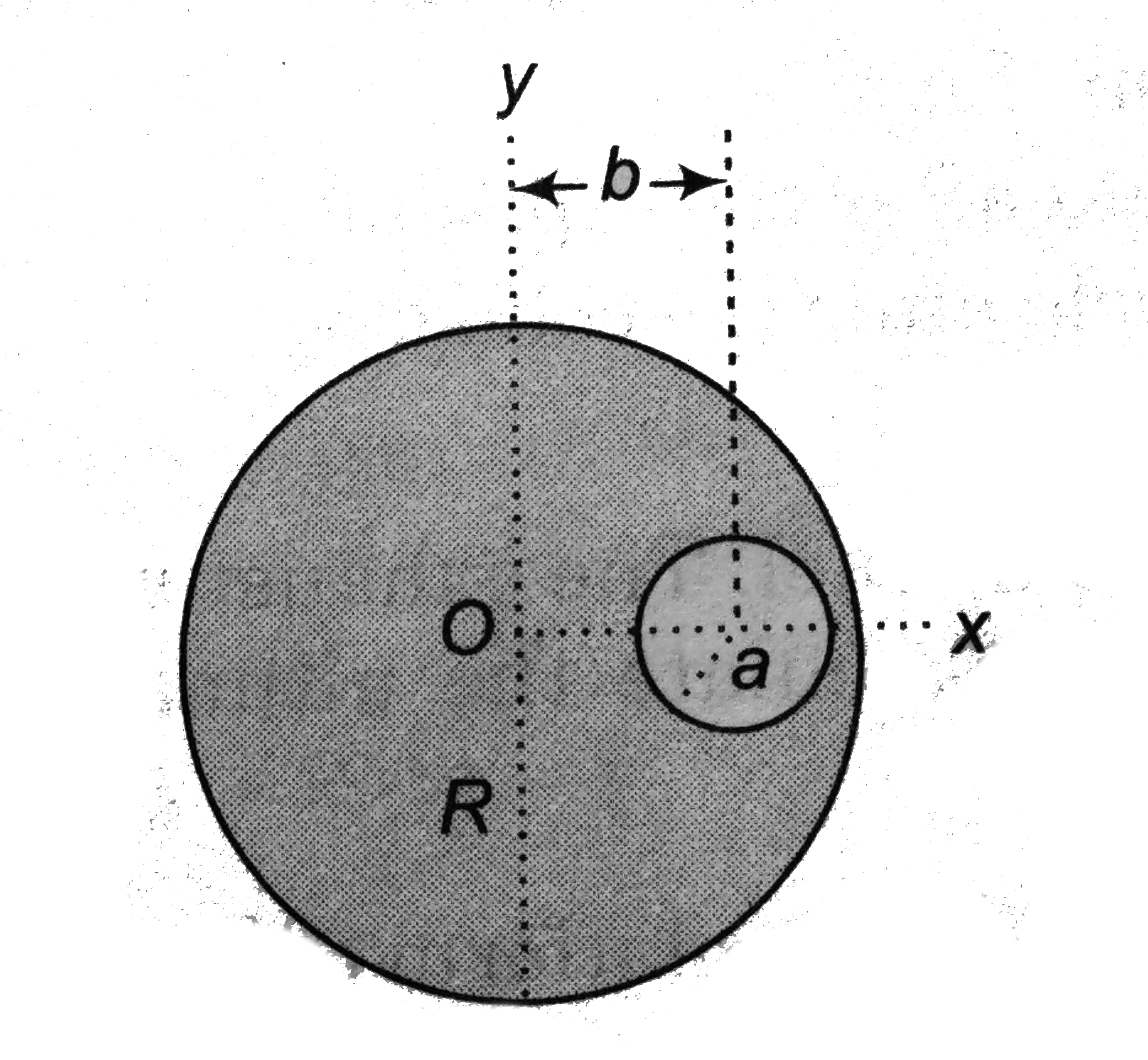
View SolutionThe uniform solid sphere shown in the figure has a spherical hole in it. Find the position of its centre of mass.
View SolutionA sphere of radius 2R has a uniform charge density p. The difference in the electric potential at r = R and r = 0 from the centre is:
View SolutionA spherical cavity is made inside a sphere of density ρ. If its centre lies at a distacne l from the centre of the sphere, show that the gravitational field strength of the field inside the cavatiy is
E=4π3Glρ
View Solution
