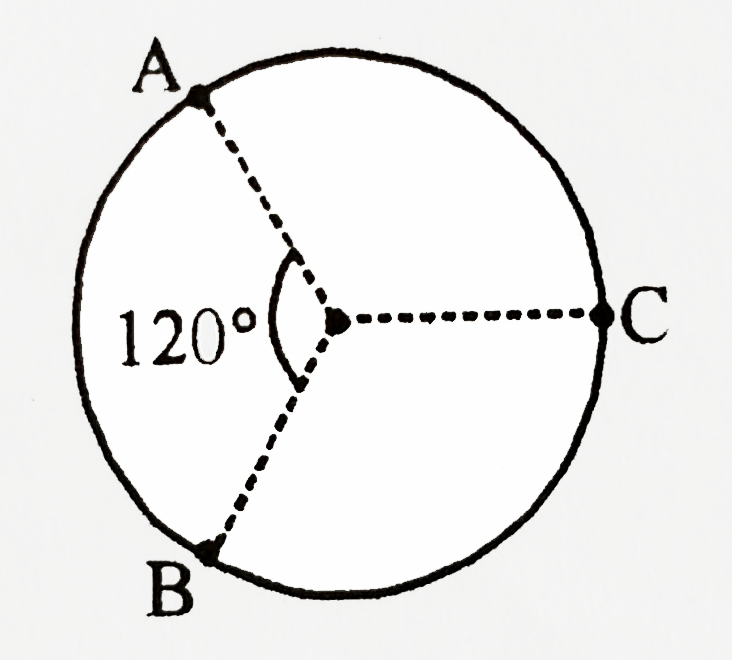
A thin shell of mass m and radius R is fixed. Two particles of same mass m are fixed at point A and B on the shell such that AB subtends an angle of 120∘ at the centre. A particle of mass m is held at point C inside the shell which is on perpendicular bisector of line AB. Find the velocity of mass at C when it reaches the opposite end of the point C on the shell under the influence of gravitational field.
The correct Answer is:[4GmR(1−1√3)]1/2
ACsin120∘=Rsin30∘
AC=√3R
Ui+Ki=Uf+KfAC'=R
Ushell+−Gm2√3R−Gm2√3R+0=−Gm2R−Gm2R+12mv2+Ushell
v=[4GmR(1−1√3)]1/2
Topper's Solved these Questions
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - A
16 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -2 [Matrix Type]
1 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)
8 Videos
- HEAT TRANSFERBOOK - BANSALCHAPTER - HEAT TRANSFEREXERCISE - Exercise
89 Videos
Similar Questions
A spherical shell of mass m and radius R is given then which of the following is incorrect for inside the sheel
View SolutionA particle of mass m is placed at a distance R from centre of a uniformly dense thin ring of mass m rand radius R on a axis passing through its centre and perpendicular to its plane. Find the speed of the particle when it reaches at the centre fo the ring due to their mutual gravitation force.
View Solution
Knowledge Check
A thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
Athe particle will execute S.H.M inside the shellBthe particle will oscillate inside the shell, but the oscillations are not simple harmonicCthe particle will not oscillate, but the speed the particle will go on increasingDnone ot theseA particle of mass m is placed inside a spherical shell, away from its centre. The mass of the shell is M.
AThe particle will move towards the centre.BThe particle will move away from the centre, towards the nearest wall.CThe particle will move towards the centres if m<M, and away from the centre if m>M.DThe particle will remain stationary.The figure shows a spherical shell of mass M. The point a is not at the centre but away from the centre of the shell. If a particle of mass m is placed at A, then
 Ait remains at restBit experiences a net force towards the centreCit experiences a net force away from the centreDNone of the above
Ait remains at restBit experiences a net force towards the centreCit experiences a net force away from the centreDNone of the above
Two particles of masses m and 2m are placed at separation L. Find the M.I. about an axis passing through the center of mass and perpendicular to the line joining the point masses.
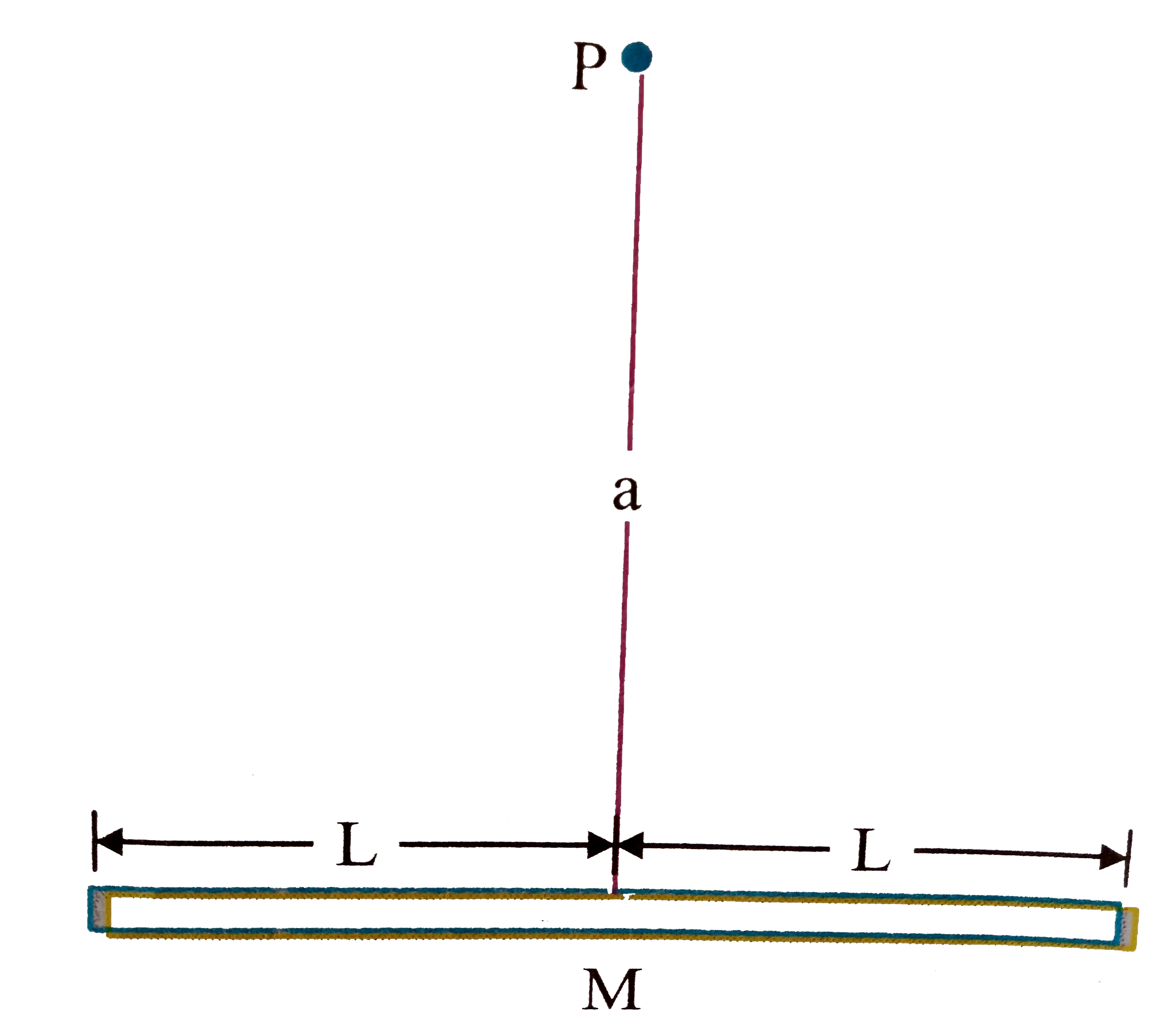
View SolutionMass M is distributed uniformly along a line of length 2L. A particle of mass m is at a point that is at a distance a above the centre of the line on the its perpendicular bisector (Point P in figure). The gravitational force that the line exert on the particle is
View SolutionA particle of mass m is located inside a spherical shell of mass M and radius R. The gravitational force of attraction between them is
View SolutionA particle of mass m oscillates inside a smooth spherical shell of radius R and starts its motion from point B. At given instant the kinetic energy of the particle is K. Then the force applied by particle on the shell at this instant is :−
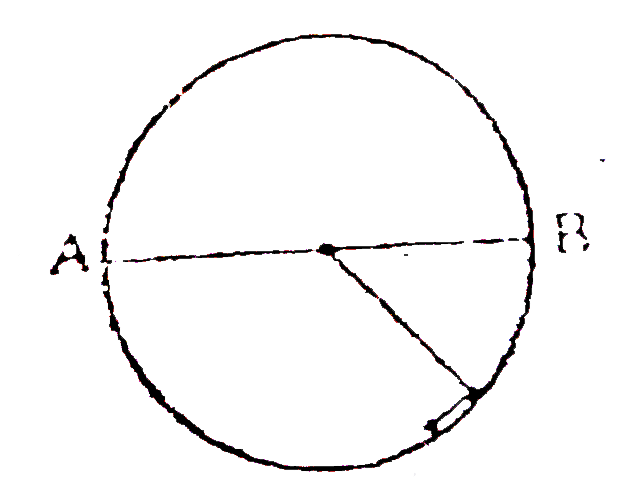
View SolutionA shell of mass M and radius R has point mass m placed at a distance r from its centre. The gravitational potential energy U(r) vs r will be
View Solution
