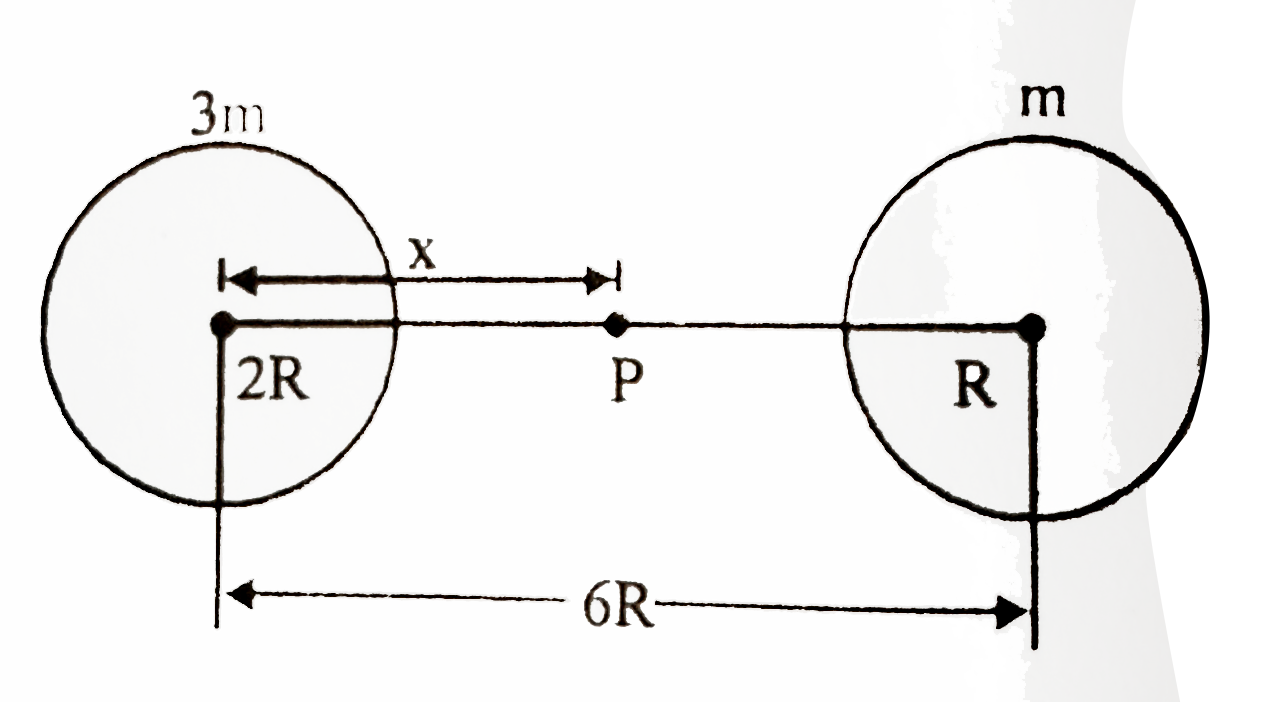
A small body of mass is projected with a velocity just sufficient to make it reach from the surface of a planet ( or radius 2R and mass 3M) to the surface of another planet (or radius R and mass M). The distance between the centres of the two spherical planets is 6R. the distance of the body from the centre of bigger planet is 'x' at any moment. During the journey, find the distance 'x' where the speed of the body is (a) maximum (b) minimum. Assume motion of body along the line joining centres of planets.
The correct Answer is:2R,3R[3−√3]
(b) From minimum velocity of projection to reach other planet body should cross the field of other. If this position velocity of projected body is minimum.
gP=−G(3m)x2+Gm(6R−x2)
0=−3Gmx2+GM(6R−x2)
3x2=1(6R−x2)⇒6R−x=±x√3
x+x√3=6R⇒(√3+1)x√3=6R
x=6√3R(√3+1)⇒x=6√3(√3−1)R2⇒x=3(3−√3)R
Topper's Solved these Questions
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -4 Section - A
Explore 16 Videos
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -4 Section - B
Explore 6 Videos
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -2 [Matrix Type]
Explore 1 Video
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)
Explore 8 Videos
- HEAT TRANSFERBook:BANSALChapter:HEAT TRANSFERExercise:Exercise
Explore 89 Videos
Similar Questions
Knowledge Check
An object is propelled vertically to a maximum height of 4R from the surface of a planet of radius R and mass M. The speed of object when it returns to the surface of the planet is -
A2√2GM5RB√GM2RC√3GM2RD√GM5RA body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
A−GH(M+m)B−GH(M−m)C−GH(mMM+m)D−GH(mMM−m)A body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to hall the escape velocity for that planet. The maximum height attained by the body is
AR/2BR/3CR/5DR/4
A body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to 1/3rd the escape velocity for the planet. The maximum height attained by the body is
View SolutionRatio of the radius of a planet A to that of planet B is r. The ratio of acceleration due to gravity for the two planets is x. The ratio of the escape velocities from the two planets is
View SolutionThe least velocity required to throw a body away from the surface of a planet so that it may not return is (radius of the planet is 6.4×106m,g=9.8m/sec2)
View SolutionA body from the surface of a planet has a escape veloctiy of 8 km/s . If the mass of the body is made twice, then the escape velocity is
View SolutionA particle at a distance r from the centre of a uniform spherical planet of mass M radius R (ltr) has a velocity of magnitude v.
View Solution

