If the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, its areal velocity is :
Lm
4Lm
L2m
2Lm
To find the areal velocity of a planet moving in a circular orbit around the Sun, we can follow these steps:
Step 1: Understand the relationship between angular momentum and areal velocity
The angular momentum L of a planet of mass m moving in a circular orbit of radius r is given by the formula:
L=mr2ω
where ω is the angular velocity of the planet.
Step 2: Define areal velocity
Areal velocity A is defined as the area swept out by the radius vector in a unit time. Mathematically, it is expressed as:
A=dAdt
For a small angle dθ, the area dA swept out by the radius vector in time dt can be approximated as:
dA=12R2dθ
where R is the radius of the circular orbit.
Step 3: Relate dA to dt
To find the areal velocity, we differentiate the area with respect to time:
A=dAdt=12R2dθdt
Here, dθdt is the angular velocity ω.
Step 4: Substitute ω in terms of L
From the angular momentum equation, we can express ω as:
ω=Lmr2
Substituting this into the equation for areal velocity gives:
A=12R2⋅LmR2
Step 5: Simplify the expression
Now, simplifying the expression:
A=12⋅Lm
Thus, the areal velocity A is:
A=L2m
Conclusion
The areal velocity of the planet is given by:
Areal Velocity=L2m
The angular momentum L of a planet of mass m moving in a circular orbit of radius r is given by the formula:
L=mr2ω
where ω is the angular velocity of the planet.
Areal velocity A is defined as the area swept out by the radius vector in a unit time. Mathematically, it is expressed as:
A=dAdt
For a small angle dθ, the area dA swept out by the radius vector in time dt can be approximated as:
dA=12R2dθ
where R is the radius of the circular orbit.
To find the areal velocity, we differentiate the area with respect to time:
A=dAdt=12R2dθdt
Here, dθdt is the angular velocity ω.
From the angular momentum equation, we can express ω as:
ω=Lmr2
Substituting this into the equation for areal velocity gives:
A=12R2⋅LmR2
Now, simplifying the expression:
A=12⋅Lm
Thus, the areal velocity A is:
A=L2m
The areal velocity of the planet is given by:
Areal Velocity=L2m
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a planet of mass m is revolving around the sun in a circular orbit of radius r with time period, T then mass of the sun is
A4π2r3/GTB4π2r3/GT2C4π2r/GTD4π2r3/G2T2A planet of mass m is moving around the sun in an elliptical orbit of semi-major axis a :
AThe total mechanical energy of the planet is varying periodically with timeBThe total energ of the planet is constant and equals −GmMs2a,Ns is mass of sunCTotal mechanical energy of the planet is constant and equals −GmMsa,M2 is mass of sunDDate is insufficient of arrice at a conclusionAll the planets move around the sun in
Acircular pathBrectangular pathCelongated elliptical pathDnone of the above
The areal velocity of the planets revolving around the sun is ………….. .
View SolutionThe motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
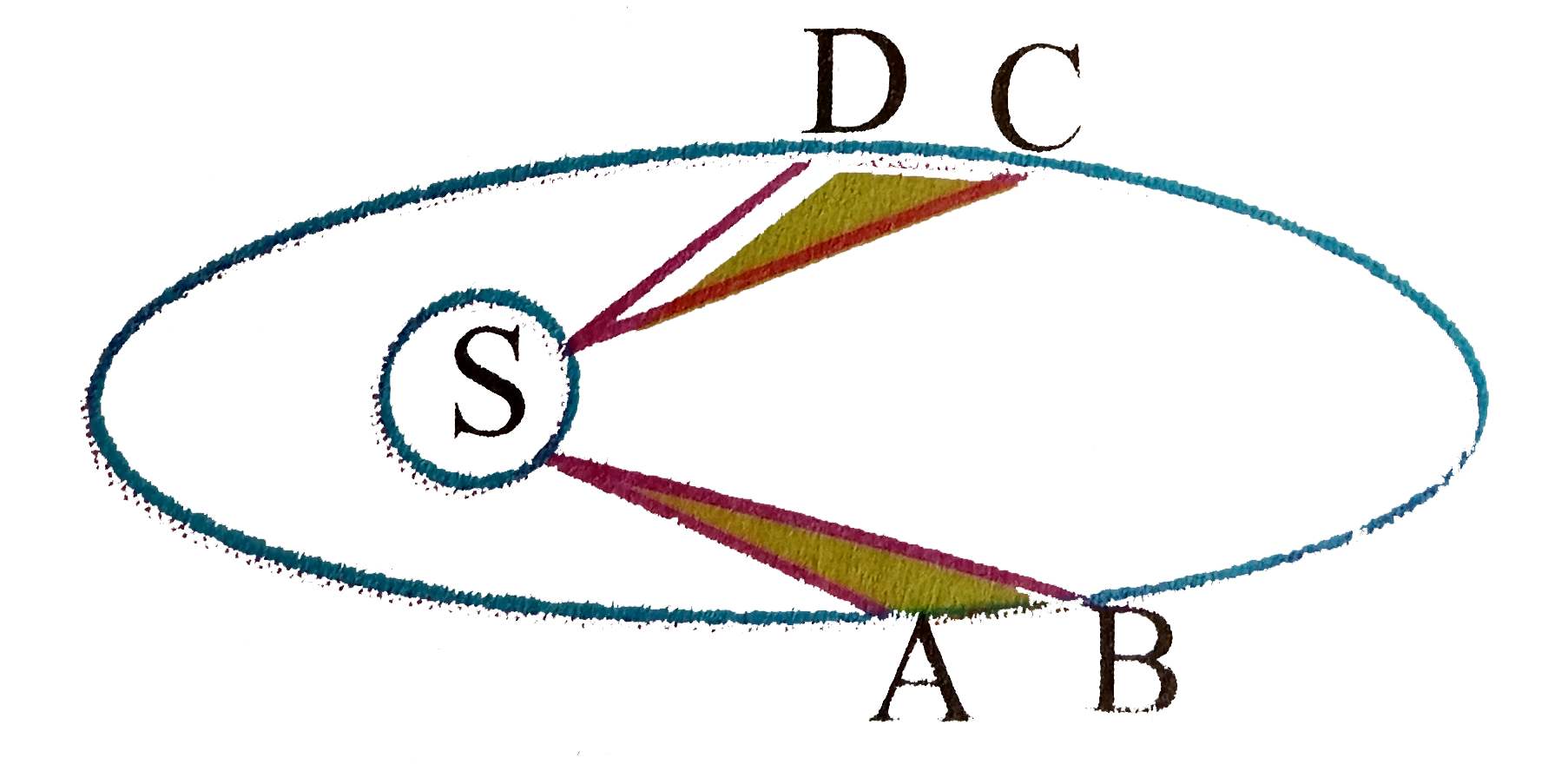
View SolutionThe motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
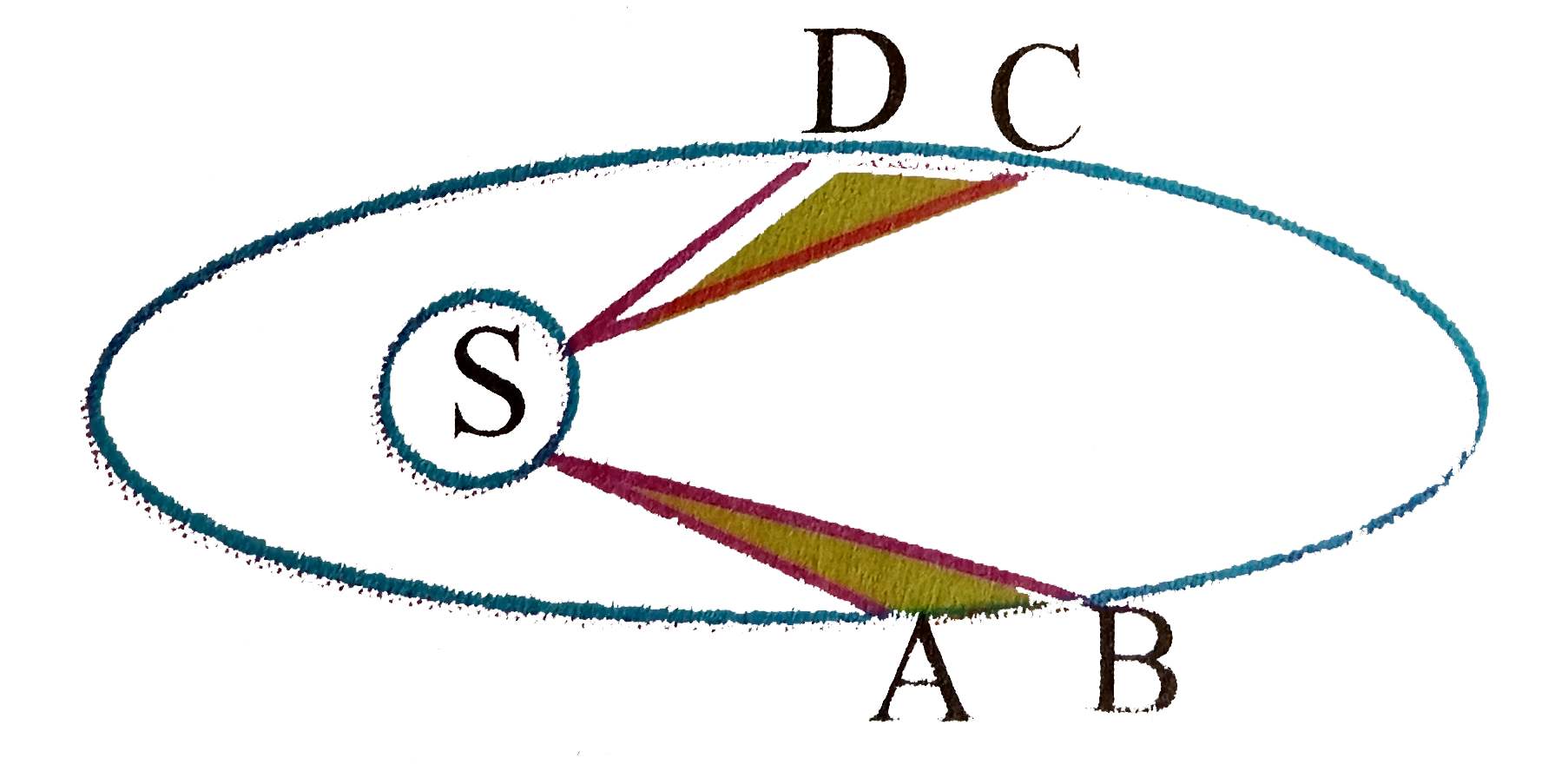
View SolutionAll the planets move around the sun in an _________
View SolutionThe areal velocity of a planet of mass m moving in elliptical orbit around the sun with an angular momentum of L units is equal to
View Solution

