An elastic ball of mass 'm' is suspended from a fixed point by an inextensible string. A small particle of same mass m, moving downwards at an angle of 37∘ with the vertical lits the ball directly with the velocity v0. If the coefficient of restitution is 4/5,
(i) find the velocity of the ball just after the impact.
(ii) determine the impulsive tension(i.e impulse) in the string at the instant of collision.
The particle after striking this ball will rebound with the velocity v exactly in the opposite direction.
Say V is the velocity attained by the ball after collision
Here the linear momentum remains conserved only in the horizontal direction.
mv0sin37∘+0=mV−mvsin37∘
Along common normal, e(v0−0)=(Vsin37∘+v)
V=(37/34)v0 and v=(11/34)v0
Impulsive tension =mv0cos37∘+mvcos37∘
=mv045+m1134v045=mv01817

Topper's Solved these Questions
Similar Questions
A person sitting at a distance of 10m from a point source of sound of power W0 writes down the following equation for the waves received by him.
y=Asin(20πx+7000πt)
(a) Determine the density of the air, if the Bulk modules of air =1.40×105Nm−2
(b) If the largest pressure amplitude tolerable to a human car is 28Pa then determine the maximum power W0 of the second source and the displacement amplitude A of the waves receive by him.
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut. (Take g=10m//s^2 )
View SolutionA ball of mass 1 kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut.
View SolutionA small ball of mass m is connected by an inextensible massless string of length with an another ball of mass M = 4m . They are released with zero tension in the string from a height h as shown in the figure. Find the time when the string becomes taut for the first time after the mass M collides with the ground. Take all collisions to be elastic.
View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
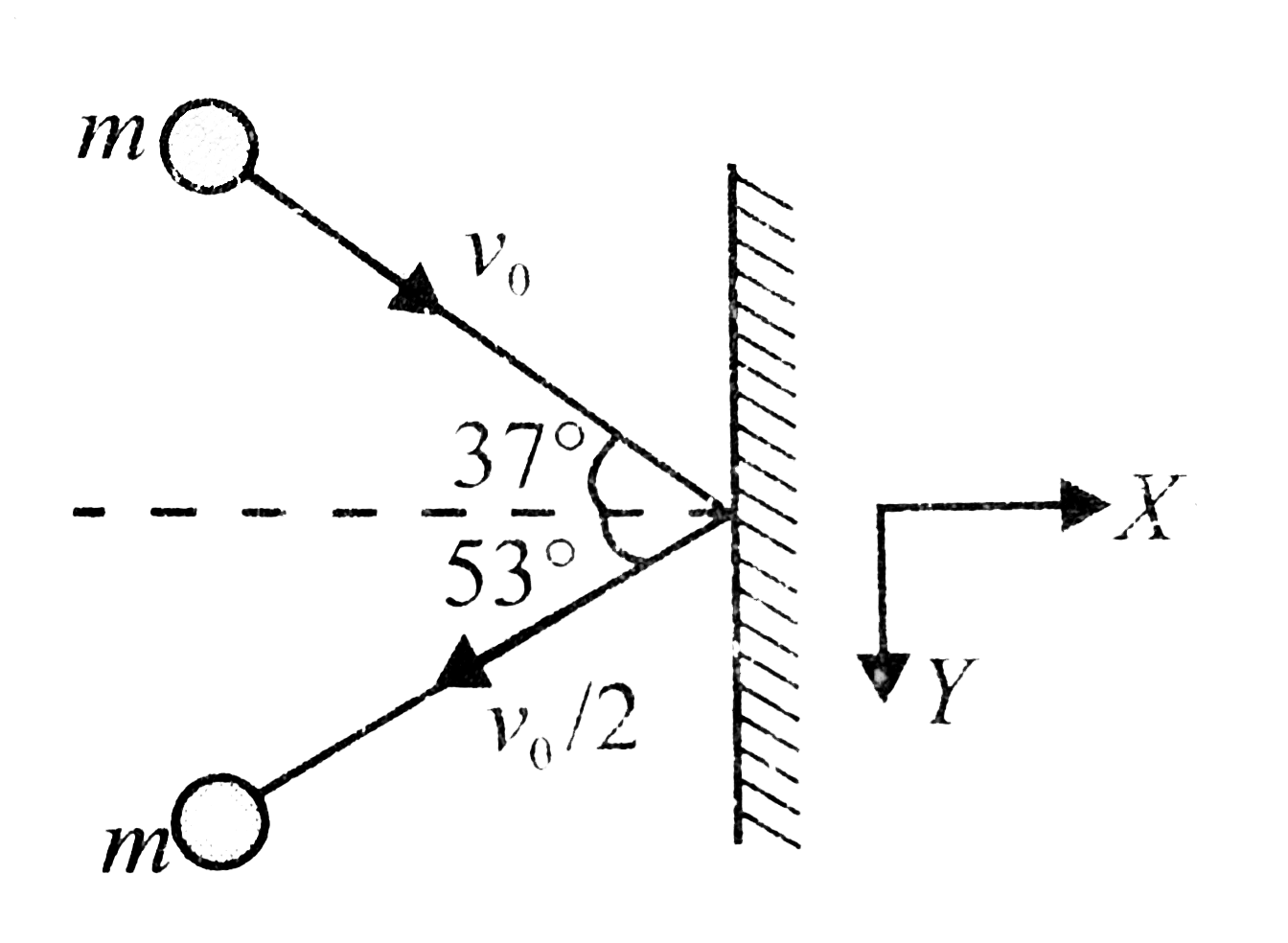
View SolutionAn elastic ball of mass 'm' is suspended from a fixed point 'O' by an inextensible string of length 2m . A small particle of mass m moving downward at angle of 37^(@) with the vertical hits the ball with v_(0) . The coefficient of restitution for collision is 4//5 . the velocity of the particle v_(0) such that ball just comoplete on revolution after the collision.
View SolutionA ball of mass m is attached to the lower end of a vertical string whose upper end is fixed. An identcial ball 'B' moving with a velocity v_(0) = 6 m//s at an angle theta = 45^(@) from vertical collides elastically with the ball 'A' as shown. The verocity of the ball 'B' just after collision is
View SolutionA ball of mass 2m impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impringes be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
View SolutionA ball of mass 1kg strink a heavy platform, elastically, moving upwards with a velocity of 5m/s. The speed of the ball just begore the collision is 10m/s downwards. Then the impulse imparted by the platform on the ball is :-
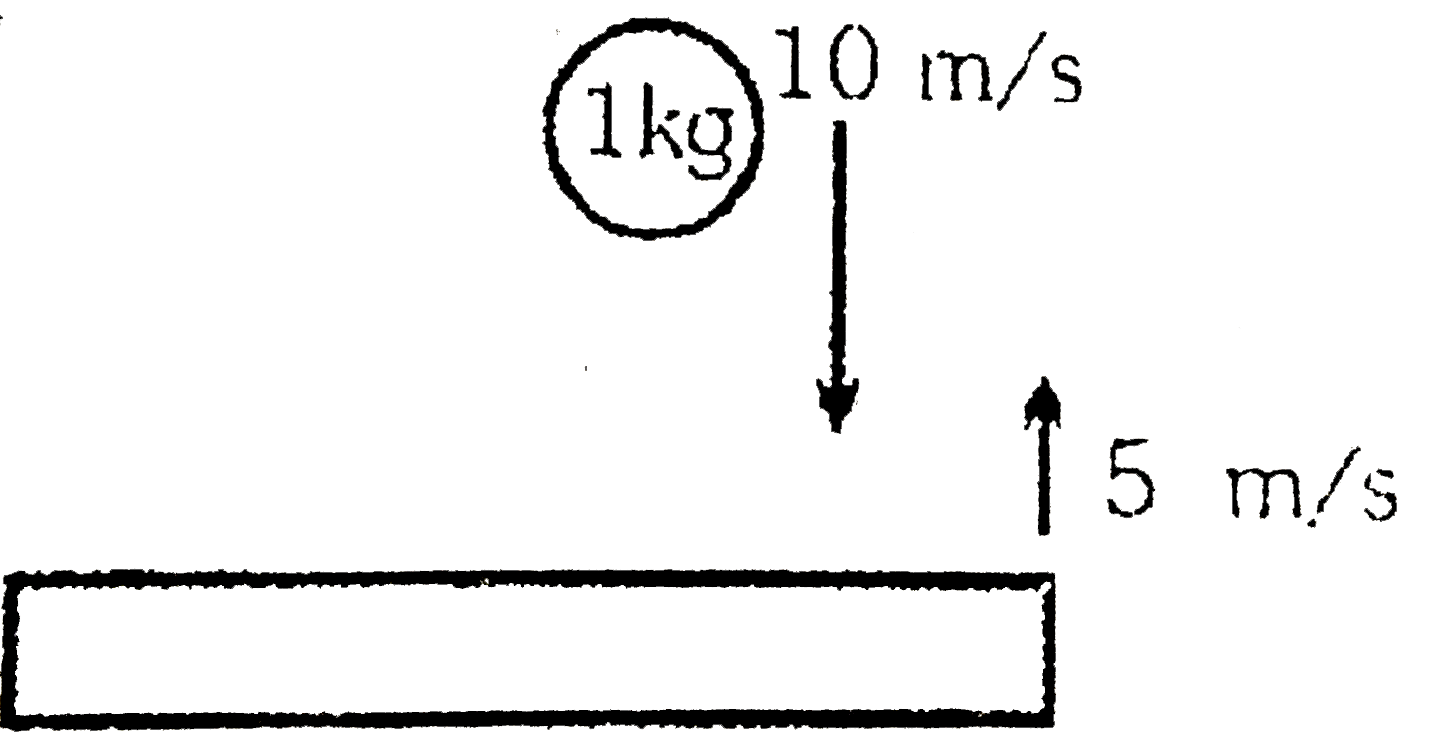
View SolutionTwo small balls A and B are interconnected by an inextensible string of legth L. Mass of ball A =m, mass of ball B = m. the balls are resting on a frictionlesss harixontal surgace , with the distance between them =3L.5 In this position ball A is suddenly given a harizontal velocity v0 perpendicular to the line joining the two balls. (see fig 4E . 18 (a))
(a) Find the speed of ball B houst after the string becomes taut
(b) find the impulse of the tension in string when the string becomes taut.
(c) Find the steady tension in string much after the string has become taut.

View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut. (Take g=10m//s^2 )
View SolutionA small ball of mass m is connected by an inextensible massless string of length with an another ball of mass M=4m. They are released with zero tension in the string from a height h as shown in the figure. Find the time when the string becomes taut for the first time after the mass M collides with the ground. Take all collisions to be elastic.

View SolutionA ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is

View SolutionA ball of mass 2m impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impinges be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
View SolutionA ball of mass 1kg strikes a heavy plarform elastically, moving upwards with a velocity of 5m/s . The speed of the ball just before the collision is 10m/s downwards. Then the impulse imparted by the platform on the ball is

View SolutionA ball of mass 2m impinges directly on a ball of mass m, which is at rest. If the velocity with which the larger ball impringes be equal to the velocity of the smaller mass after impact then the coefficient of restitution :-
View Solution

