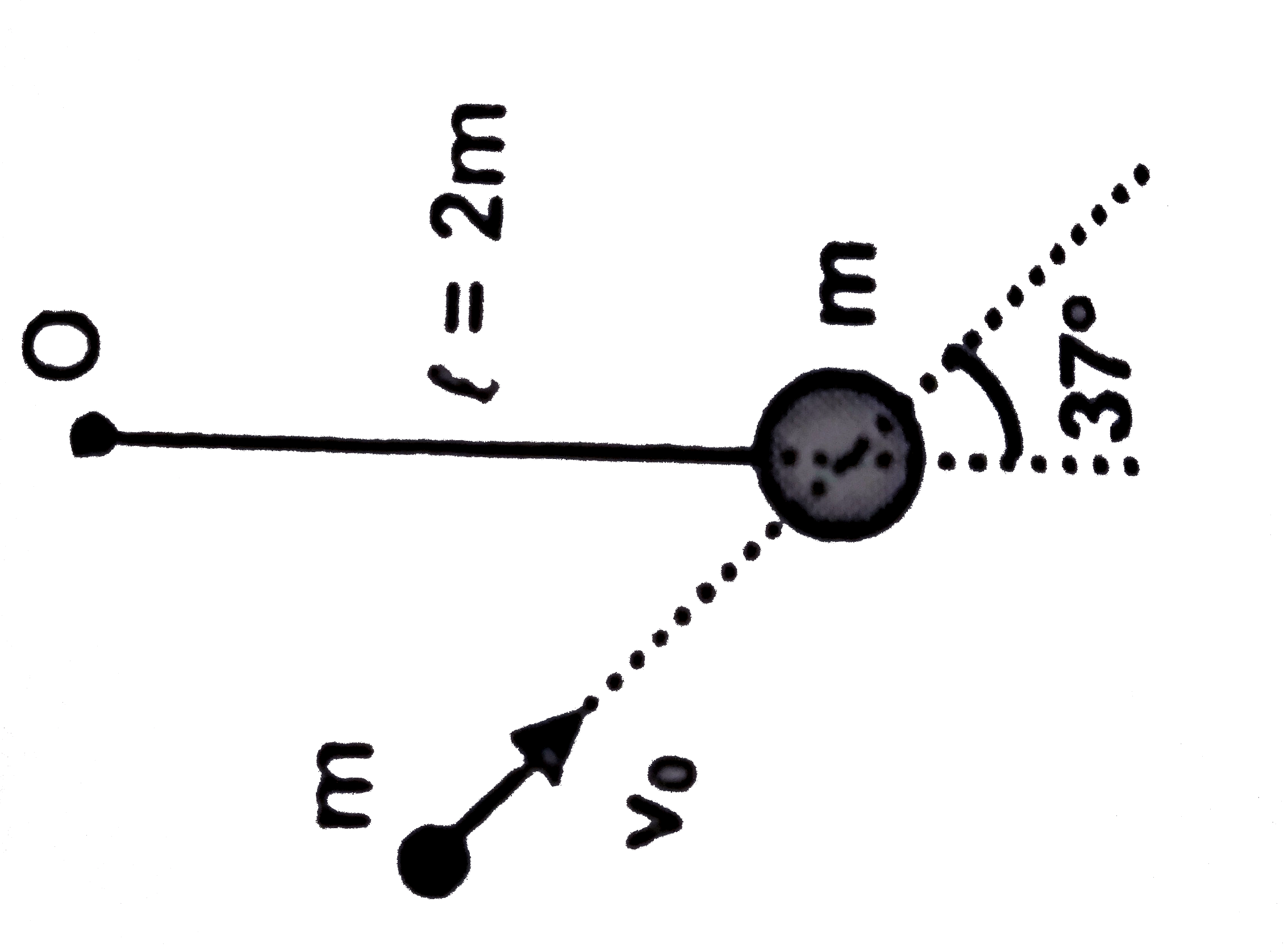
An elastic ball of mass 'm' is suspended from a fixed point 'O' by an inextensible string of length . A small particle of mass m moving downward at angle of with the vertical hits the ball with . The coefficient of restitution for collision is . the velocity of the particle such that ball just comoplete on revolution after the collision.
The correct Answer is:D
and are the velocity after the collision.
....(i)
...(ii)
From (i) and (ii)

Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
An elastic ball of mass 'm' is suspended from a fixed point by an inextensible string. A small particle of same mass m, moving downwards at an angle of 37∘ with the vertical lits the ball directly with the velocity v0. If the coefficient of restitution is 4/5,
(i) find the velocity of the ball just after the impact.
(ii) determine the impulsive tension(i.e impulse) in the string at the instant of collision.
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View Solution
Knowledge Check
A particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
A1BmMCM−mM+mDmM+mA ball of mass 1kg is dropped from a height of 3.2m on smooth inclined plane. The coefficient of restitution for the collision is e=1/2. The ball's velocity become horizontal after the collision.
 Athe angle θ=tan−1(1√2)BThe speed of the ball after the collision =4√2ms−1CThe total loss in kinetic energy during the collision is 8J.DThe ball hits the inclined plane again while travelling vertically downward.
Athe angle θ=tan−1(1√2)BThe speed of the ball after the collision =4√2ms−1CThe total loss in kinetic energy during the collision is 8J.DThe ball hits the inclined plane again while travelling vertically downward.A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1
A particle of mass m moving with a constant velocity v hits another identical stationary particle. If coefficient of restitution is e then ratio of velocities of two particles after collision is
View SolutionA particle of mass m moving with a constant velocity v hits another identical stationary particle. If coefficient of restitution is e then ratio of velocities of two particles after collision is
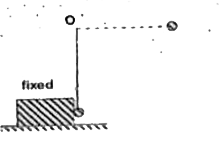
View SolutionA small ball is suspended from a fixed point 'O' by means of a light and inextensible string of length 'l'. The ball is first taken aside such that string becomes horizontal and then released from rest. At the borrom it collides with a fixed obstacle. The co-efficient of restitution is 'e'. Find the maximum angular deflection of the string after nth collision.
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View Solution

