A uniform solid sphere of mass m and radius 'R' is imparted an initial velocity v0 and angular ω0=2v0R and then placed on a rough inclined plane of inclination 'theta' and coefficient of friction μ=2tanθ as shown. The time after which the sphere will start rolling without slipping is

v02gsinθ
v04gsinθ
v06gsinθ
v08gsinθ
The correct Answer is:C
N=mgcosθ
fk=μN=2tanθtmgcosθ=2mgsinθ
fk−mgsinθ=ma
2mgsinθ−mgsinθ=ma
∴a=gsinθ
Now, τcm=Icmα
fkR=25mR2α
2mgsinθ=25mRα
α=5gsinθR
Where the rolling without slipping starts
v=ωR
v0+at=(ω0−αt)R
v0+gsinθt=ω0R−5gsinθt
v0+6gsinθt=2v0
∴=v06gsinθ
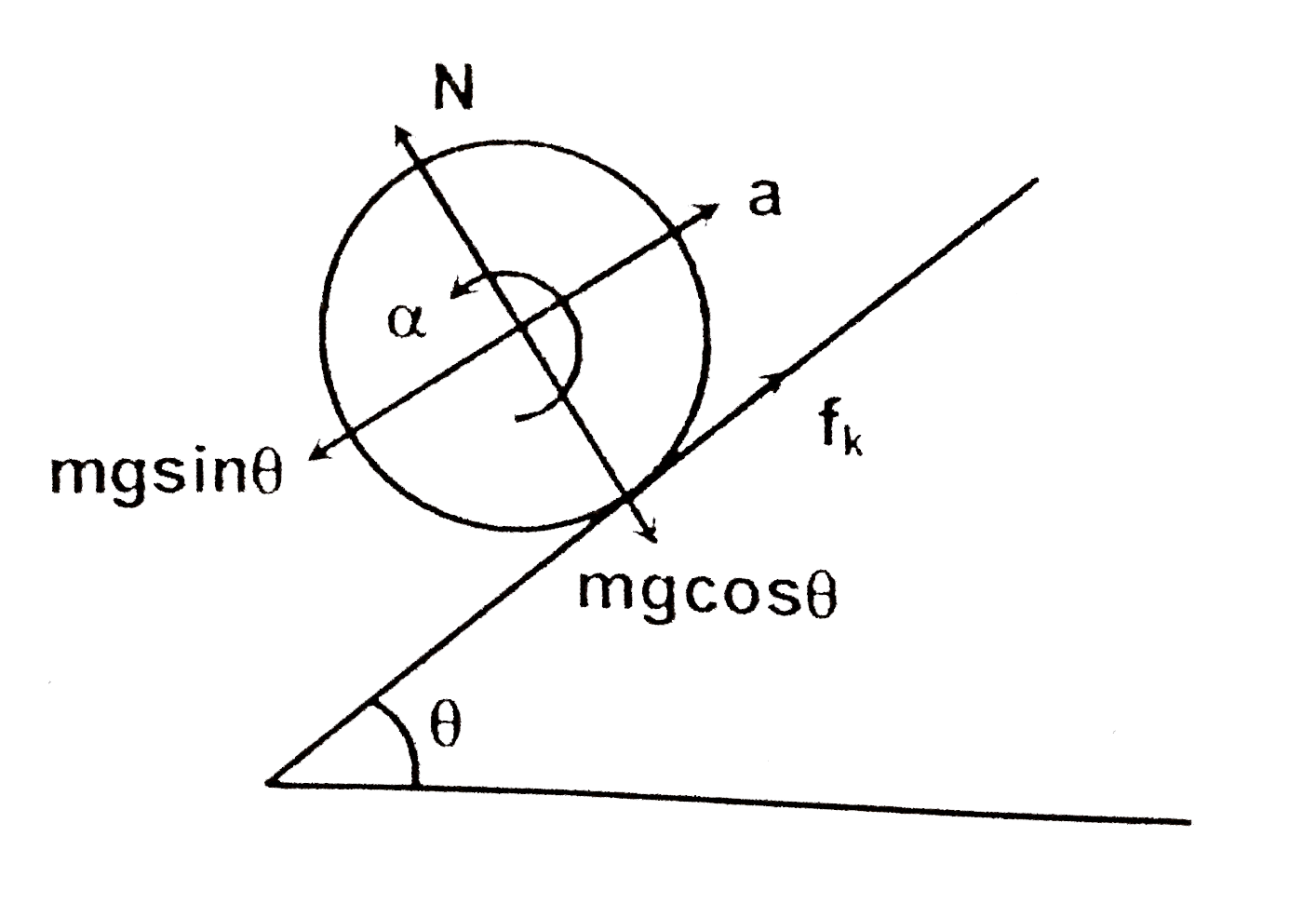
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.

View SolutionA cylinder of mass m radius R is spined to a clockwise angular velocity ωo and then gently placed on an inclined plane for which coefficient of friction μ=tanθ,θ is the angle of inclined plane with the horizontal. The centre of mass of cylinder will remain stationary for time

View Solution
Knowledge Check
A sphere of mass M rolls without slipping on the inclined plane of inclination θ. What should be the minimum coefficient of friction, so that the sphere rolls down without slipping ?
A2/5tanθB2/7tanθC5/7tanθDtanθA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
AFriction opposes its translationBFriction supports rotation motionCOn decreasing θ, frictional force decreasesDAll of theseA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
Africtional force is always μmgcosθBfriction is a dissipative forceCby decreasing θ, frictional force decreasesDfrictiona opposes translation and supports rotation.
A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
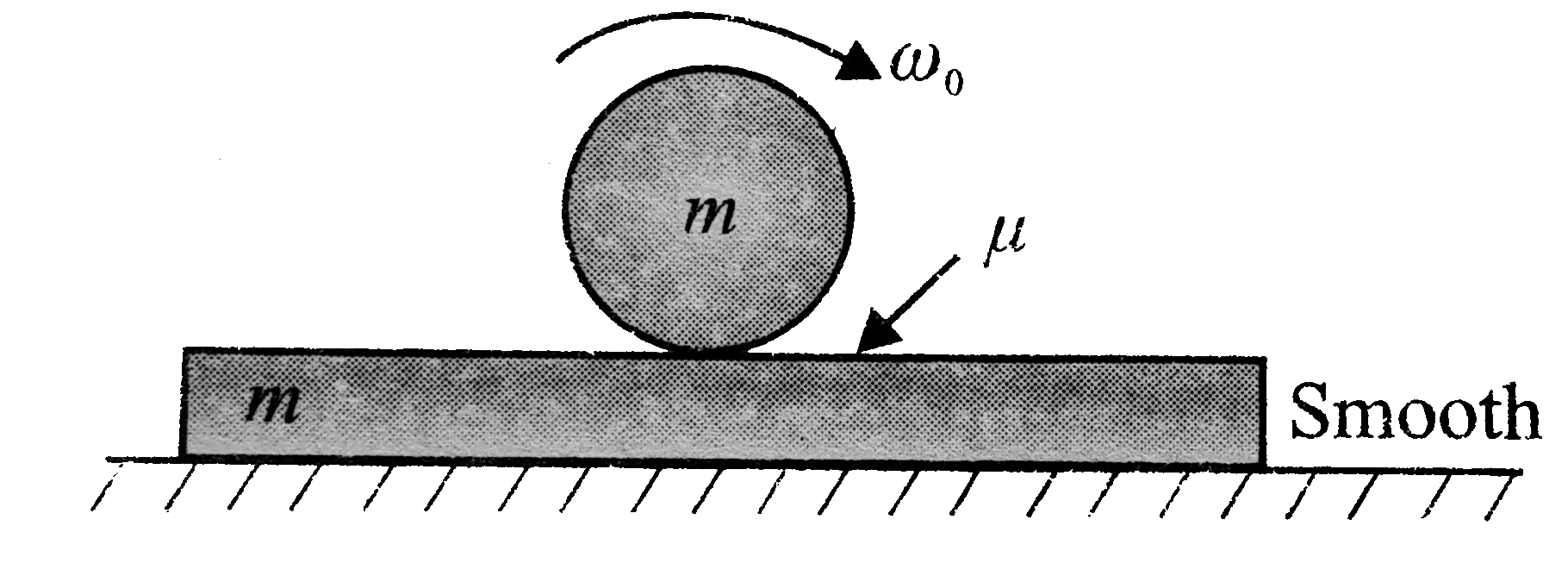
Find the velocity of the sphere after the pure rolling starts
View SolutionA ring of mass M and radius R is released on an inclined as shown. If the coefficient of friction μ<12tanθ, then during a displacement l:
View SolutionA solid cylinder is rolling without slipping on a plane having inclination θ and the coefficient of static friction μs. The relation between θ and μs is
View Solution
