A thin uniform spherical shell of mass m=2kg and radius R=10cm is placed on a rough horizontal surface with a coefficient of friction μ=0.4. A horizontal force 'F' is applied to the spherical shell at a height R/3 ablove the centre as shown. The maximum magnitude of the applied force 'F' for which the spherical shell will be rolling without slipping is (taking g=10m/a2 )
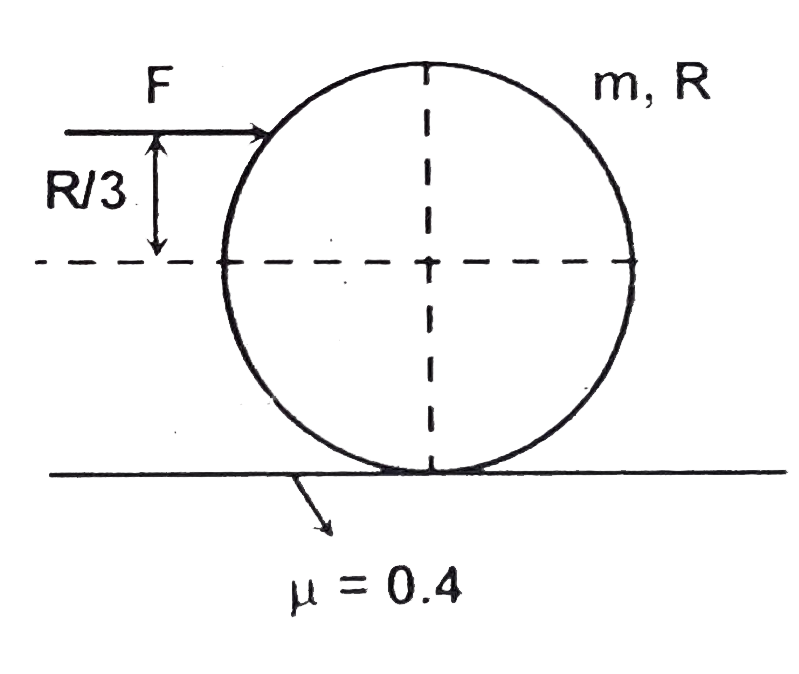
20N
30N
40N
60N
The correct Answer is:C
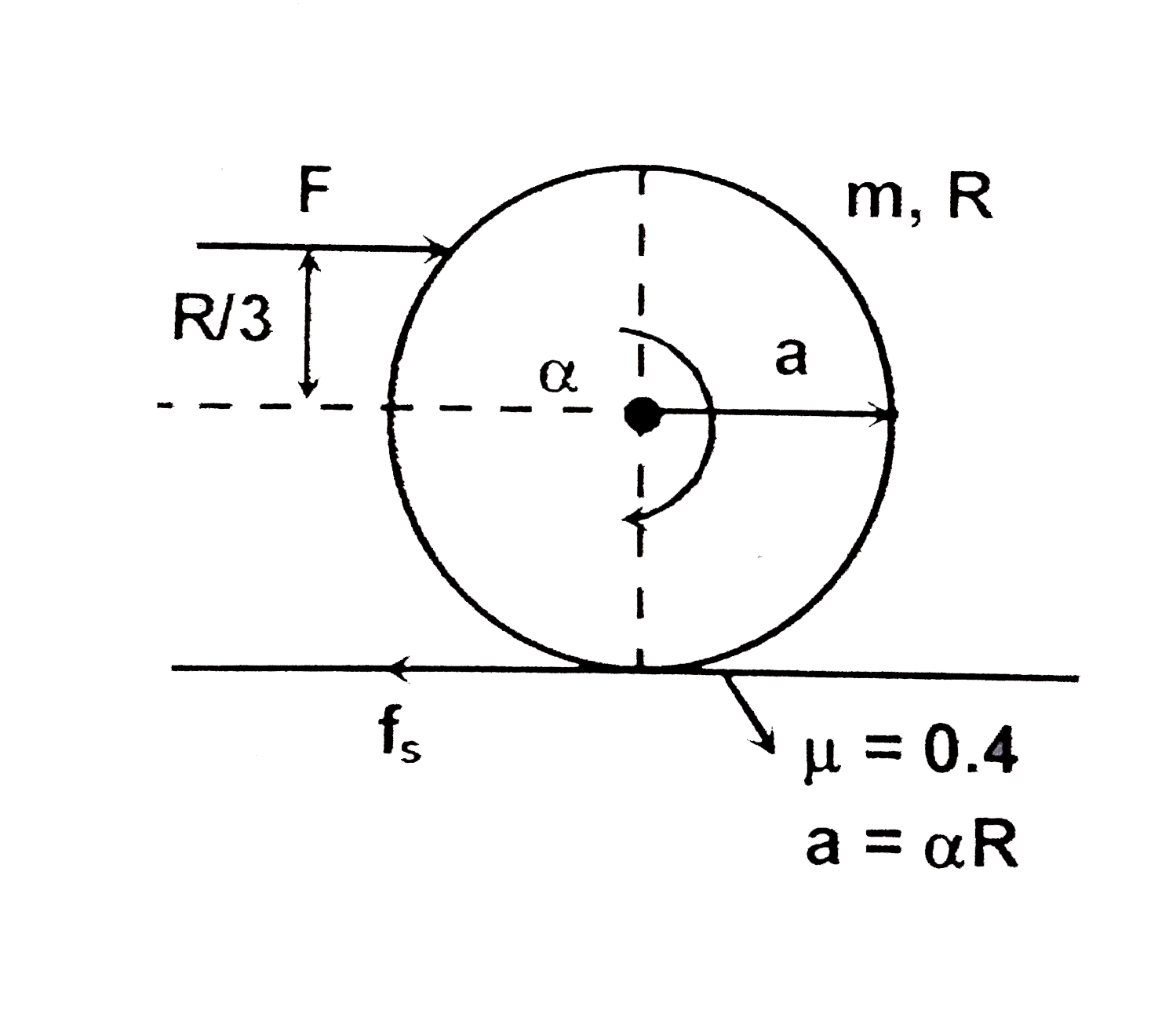
F−fs=ma …..(i)
FR3+fsR=23mR2α
F3+fs=23ma [since, a=Rα] …..(i)
Solving (i) and (ii), we get
4F3=53ma
a=4F5m
Now, from equation (i)
fs=F−ma=F−4F5=F5
Hence, fs≤μN
F/5≤μN
F≤5μmg
∴Fmax=5×0.4×20=40N
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A solid cylindrical roller of mass M and radius R is rolled on a rough horizontal surface by applying a horizontal force F at the top most point. The frictional force between the roller and the surface, is
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View Solution
Knowledge Check
A block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .
 A5.73m/sec2B8.0m/sec2C3.17m/sec2D10.0m/sec2
A5.73m/sec2B8.0m/sec2C3.17m/sec2D10.0m/sec2
A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,AThe maximum possible acceleration of sphere is FMBThe maximum possible acceleration of sphere is 10F7MCThe magnitude of friction force acting on the sphere is zero if h=2R5DThe magnitude of friction force acting on the sphere is zero h=3R4.A block of mass m is placed on a rough horizontal surface. The coefficent of friction between them is μ. An external horizontal force is applied to the block and its magnitude is gradually increased. The force exerted by the block on the surface is R.
AThe magnitude of R gradually increase.BR≤mg√μ2+1.CThe angle made by R with the vertical will gradually increase.DThe angle made by R with the vertical ≤tan−1μ.
A block of mass m is lying on horizontal surface of coefficient of friction μ. A force is applied to the block at an angle θ with the horizontal. The block will move with a minimum force F if
View SolutionA thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
View SolutionA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and 10m/s−2. If a horizontal force of 50N is applied on the block, the frictional force is
View SolutionA massless string is wrapped around a hollow cylinder having mass m and radius r. The cylinder is kept on a rough horizontal surface (coefficient of friction is μ). A constant force F is applied as shown in the figure. In case of pure rolling, the friction force acting on the bottom most point of the cylinder is
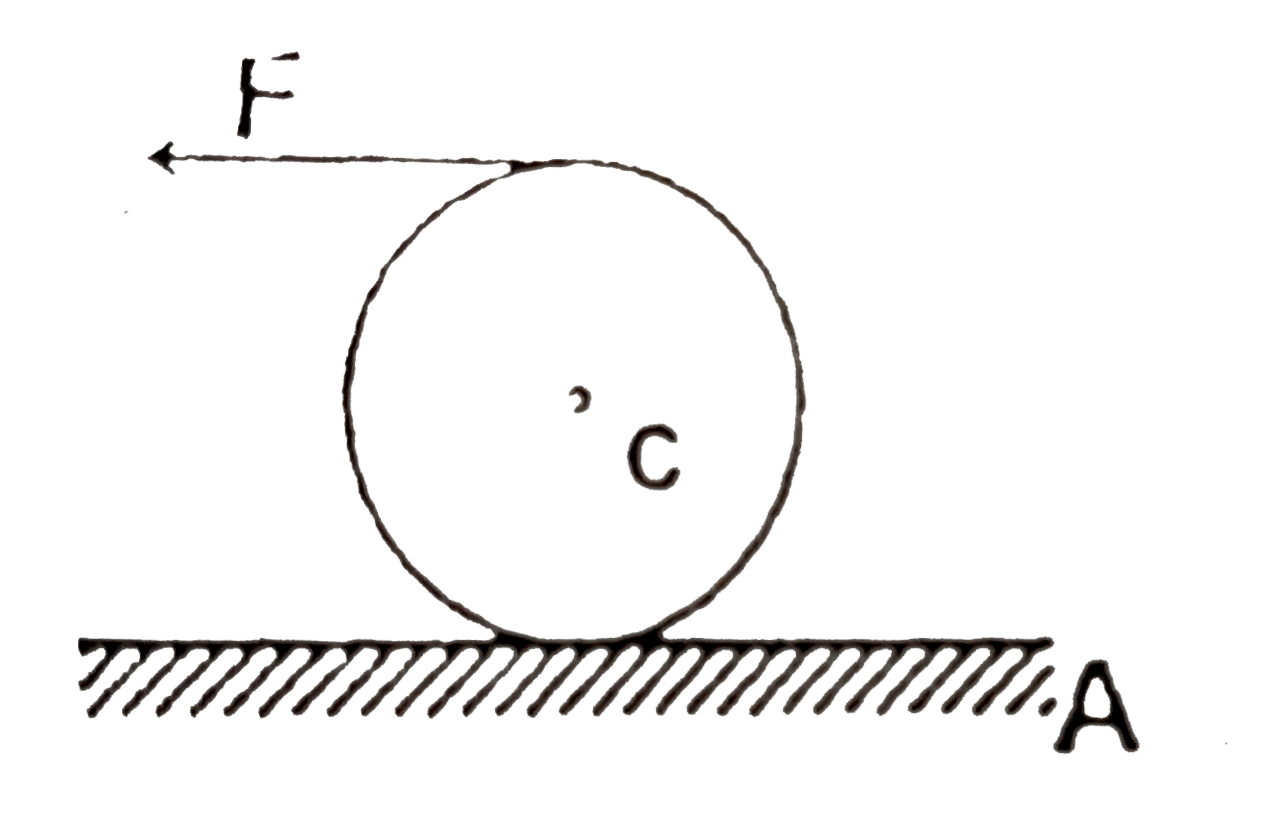
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View Solution
