A glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
The correct Answer is:0.5 m/s, 1.5 m/s
To solve the problem of the collision between two identical glass balls, we will use the principles of conservation of momentum and the coefficient of restitution. Here’s a step-by-step solution:
Step 1: Define the Initial Conditions
- Let the mass of each glass ball be m.
- The initial velocity of the first ball (moving towards the second) is v0=2m/s.
- The second ball is initially at rest, so its initial velocity u2=0m/s.
Step 2: Apply Conservation of Momentum
The conservation of momentum states that the total momentum before the collision is equal to the total momentum after the collision. Thus, we can write:
mv0+mu2=mv1+mv2
Substituting the known values:
m(2)+m(0)=mv1+mv2
Since the masses are identical, we can cancel m from the equation:
2=v1+v2(Equation 1)
Step 3: Use the Coefficient of Restitution
The coefficient of restitution e is defined as the ratio of the relative velocity of separation to the relative velocity of approach. Mathematically, it can be expressed as:
e=v2−v1v0−u2
Substituting the known values:
0.5=v2−v12−0
This simplifies to:
0.5=v2−v12
Multiplying both sides by 2 gives:
v2−v1=1(Equation 2)
Step 4: Solve the Equations Simultaneously
Now we have two equations:
1. v1+v2=2 (Equation 1)
2. v2−v1=1 (Equation 2)
From Equation 2, we can express v2 in terms of v1:
v2=v1+1
Substituting this expression for v2 into Equation 1:
v1+(v1+1)=2
This simplifies to:
2v1+1=2
Subtracting 1 from both sides:
2v1=1
Dividing by 2:
v1=0.5m/s
Step 5: Find v2
Now substituting v1 back into Equation 2 to find v2:
v2=v1+1=0.5+1=1.5m/s
Final Answer
The velocities of the glass balls just after the collision are:
- v1=0.5m/s (first ball)
- v2=1.5m/s (second ball)
- Let the mass of each glass ball be m.
- The initial velocity of the first ball (moving towards the second) is v0=2m/s.
- The second ball is initially at rest, so its initial velocity u2=0m/s.
The conservation of momentum states that the total momentum before the collision is equal to the total momentum after the collision. Thus, we can write:
The coefficient of restitution e is defined as the ratio of the relative velocity of separation to the relative velocity of approach. Mathematically, it can be expressed as:
Now we have two equations:
1. v1+v2=2 (Equation 1)
2. v2−v1=1 (Equation 2)
Now substituting v1 back into Equation 2 to find v2:
The velocities of the glass balls just after the collision are:
- v1=0.5m/s (first ball)
- v2=1.5m/s (second ball)
Topper's Solved these Questions
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - II
Explore 17 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (OBJECTIVE) Level - I
Explore 45 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) Level - I (True/False)
Explore 2 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:ASSERTION REASONING TYPE
Explore 1 Video
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:Comprehension -4
Explore 3 Videos
Similar Questions
A ball of mass 2kg moving with speed 5m/s collides directly with another ball of mass 3kg moving in the same direction with speed 4m/s. The coefficient os restitution is 2/3. Find the velocities of both ball after the collision.
View SolutionBall 1 collides with another identical ball at rest. For what value of coefficient of restitution e, the velocity of second ball becomes two times that of 1 after collision? _____.
View Solution
Knowledge Check
A glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
A√e2a2+b2 at angle tan−1(aeb) to the verticalB√a2+e2b2 at angle tan−1(aeb) to the verticalC√a2+b2e2 at angle tan−1(eab) to the verticalD√a2e2+b2 at angle tan−1(aeb) to the verticalA ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1An elastic ball of mass 'm' is suspended from a fixed point 'O' by an inextensible string of length 2m. A small particle of mass m moving downward at angle of 37∘ with the vertical hits the ball with v0. The coefficient of restitution for collision is 4/5. the velocity of the particle v0 such that ball just comoplete on revolution after the collision.
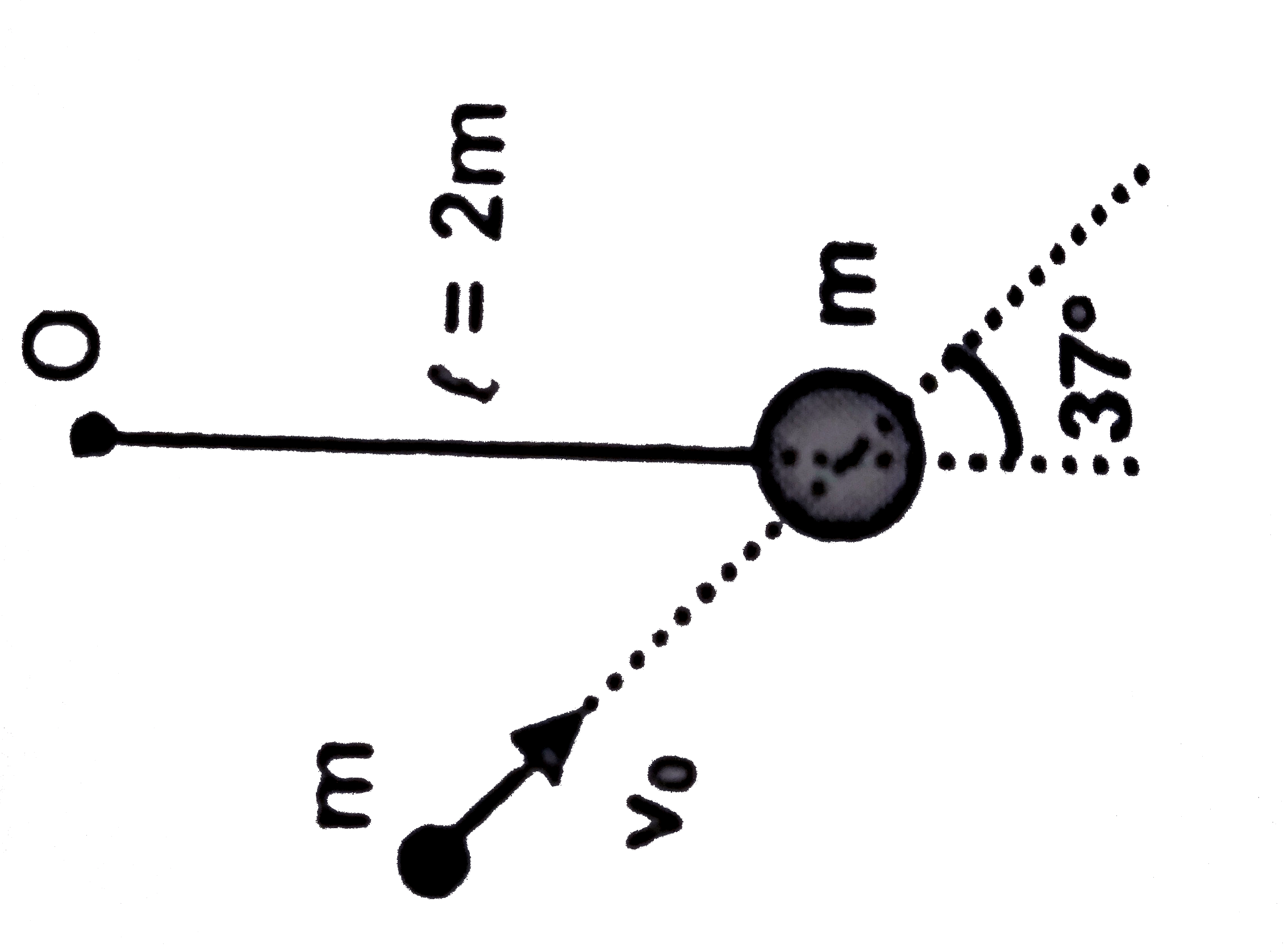 A17027m/sB8527m/sC68027m/sD34027m/s
A17027m/sB8527m/sC68027m/sD34027m/s
(i) A block of mass m moving towards right with a velocity V strikes (head on) another block of mass M which is at rest connected to a spring. The coefficient of restitution for collision between the blocks is e = 0.5.
Find the ratio Mm for which the subsequent compression in the spring is maximum. There is not friction.

Ball A collides head on with another identical ball B at rest. Find the coefficient of restitution if ball B has 80% of the total kinetic energy of the system after collision.
View SolutionA small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.

View SolutionBall 1 collides with an another identical ball 2 at rest as shown in figure. For what value of coefficient of restitution e, the velocity of ball 2 becomes two times that of ball I after collision?

View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View SolutionA ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.
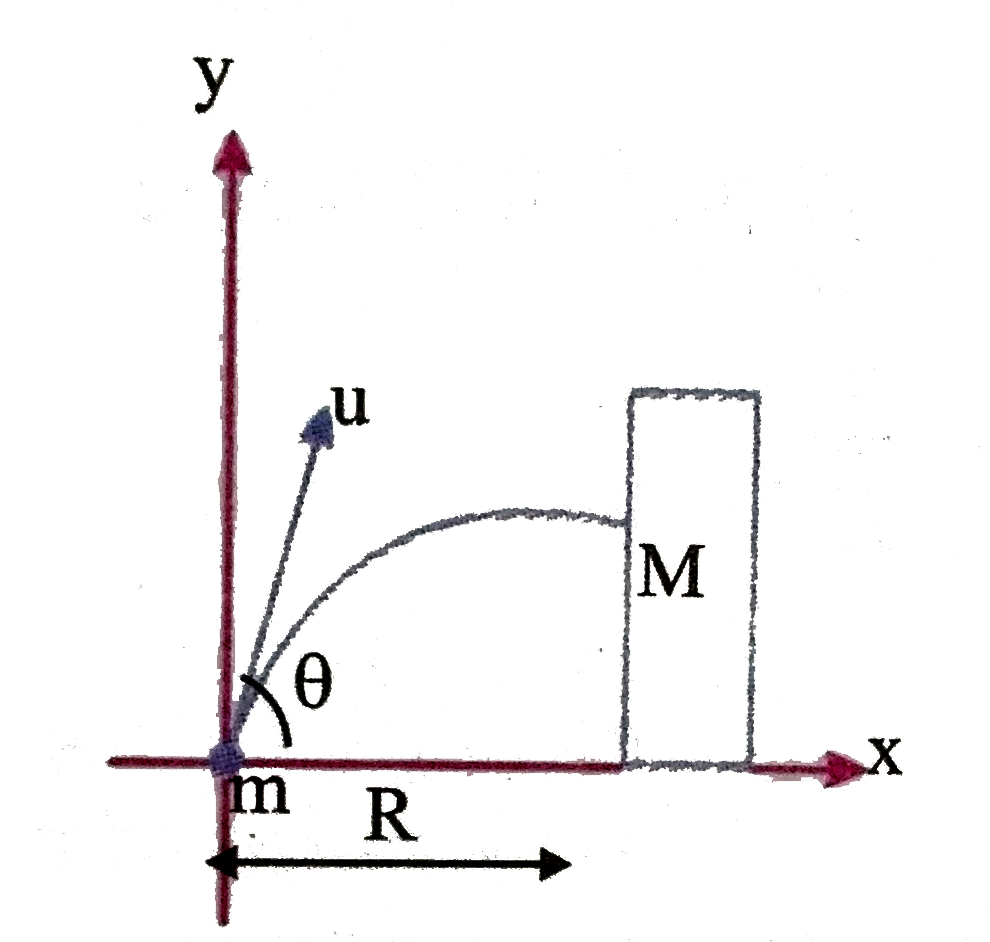
FInd the velocity of the ball after collision
View Solution