A ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.
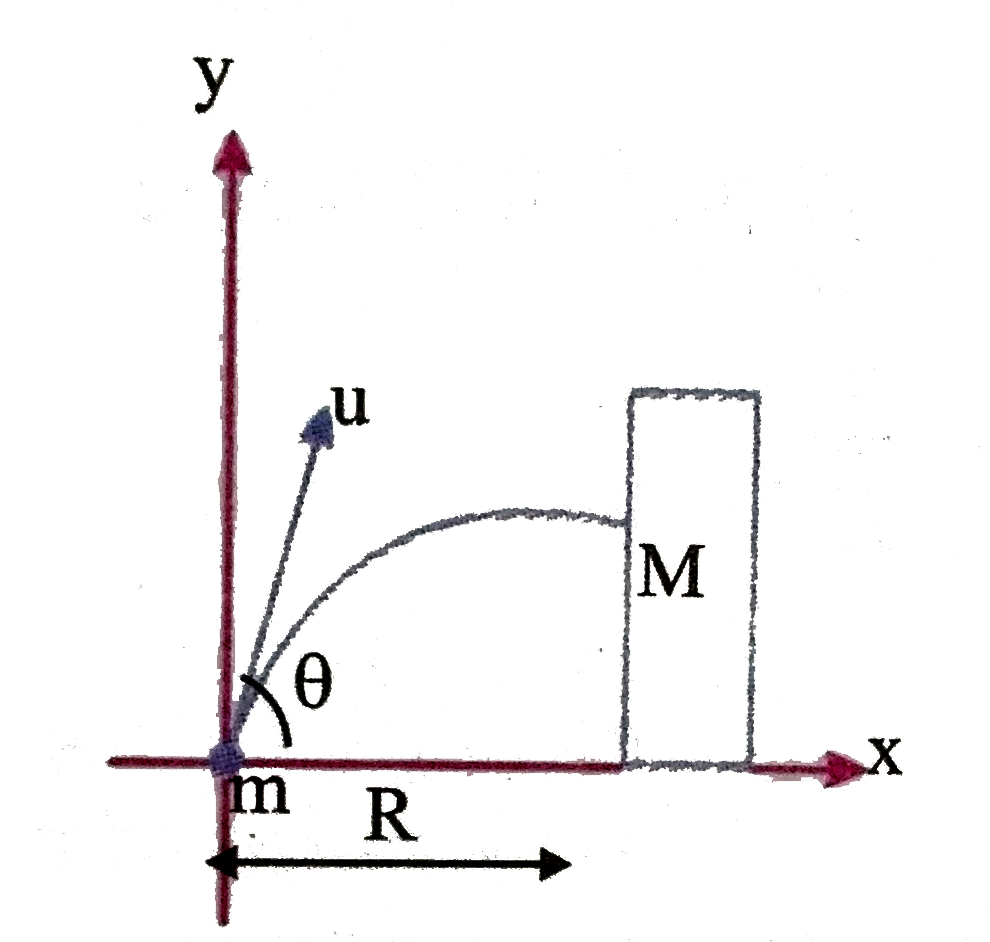
FInd the velocity of the ball after collision
(m−eMM+m)ucosθ
(M−emM+m)ucosθ
(m+eMM+m)usinθ
(m−eMM+m)usinθ
The correct Answer is:A

Recoil velocity of ball after collision v(m−eMM+m)ucosθ
From v1=(M1−eM2M1+m2)+2m2u2m1+m2
R'R=vucosθ=(eM−mM+m),R'=(eM−mM+m)R
The ball hit at a point 'P' at a distance
Δx=R−R'=R(1−(eM−mM+m))
=R(M(1−e)+2mM+m)
Topper's Solved these Questions
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Subjective type Questions
Explore 9 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Level-I (H.W)
Explore 52 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Multiple Answer
Explore 11 Videos
- CIRCULAR MOTIONBook:NARAYNAChapter:CIRCULAR MOTIONExercise:LEVEL II(H.W)
Explore 51 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
Similar Questions
A glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionA body of mass m is projected with a velocity u at an angle θ with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
View Solution
Knowledge Check
A ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.

Find the position at which the ball meets the x-axis from the originA(M(1−e)+2mM+m)RB(m(1−e)+2MM+m)RC(M+m(1−e)M+m)RD(M(1−e)+2m2(M+m))RA ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.

Find the horizontal distance travelled by the ball before collision.Au22sinθcosθgBu2sinθcosθgCu2sinθcosθ2gDu2sinθcosθ4gA ball is projected with initial velocity u at an angle θ to the horizontal. Then horizontal displacement covered by ball as it collides third time to the ground would be, if coefficient of restitution is e :
 A(1+e)u2sin2θgBeu2sin2θgC(1−e)u2sin2θgD(1+e+e2)u2sin2θg
A(1+e)u2sin2θgBeu2sin2θgC(1−e)u2sin2θgD(1+e+e2)u2sin2θg
A small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.

View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionA ball of mass 2kg moving with speed 5m/s collides directly with another ball of mass 3kg moving in the same direction with speed 4m/s. The coefficient os restitution is 2/3. Find the velocities of both ball after the collision.
View SolutionA glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View Solution

