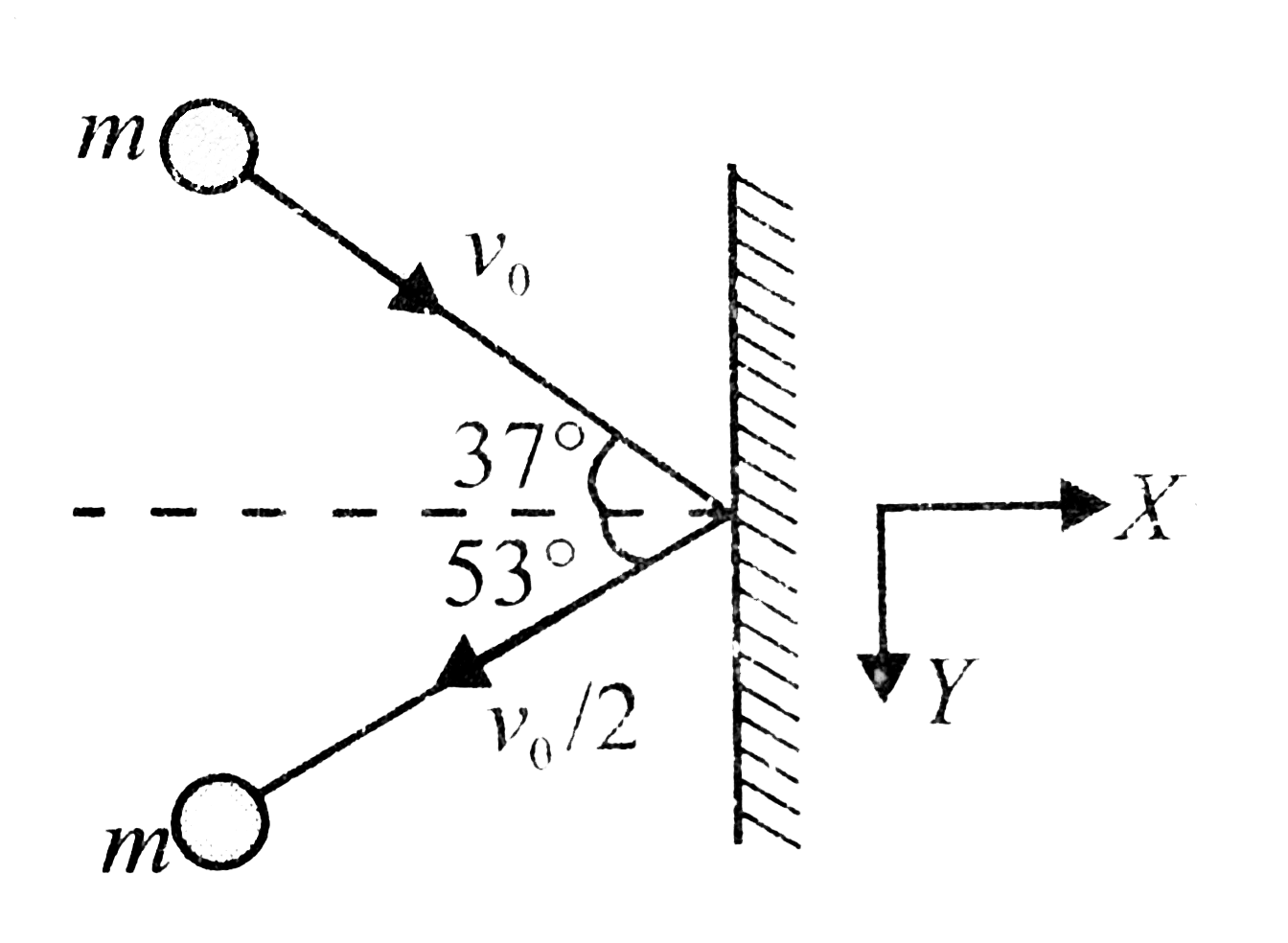
A ball of mass m moving with velocity v0 collides with a wall as shown in Fig. After impact it rebounds with a velocity' (v0)/2The component of impulse acting on the ball along the wall is
mv02ˆj
−mv02ˆj
−mv05ˆj
none of these
The correct Answer is:C
Component of initial momentum along the wall is
Piy=mv0sin37∘ˆj
component of final momentum along the wall is
Piy=(mv0)sin37∘ˆj
Pfy=mv02sin53∘ˆj
So, component of impulse along the wall is Jy=Pfy−Piy
mv02×45−mv01×35ˆj=−mv05ˆj
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
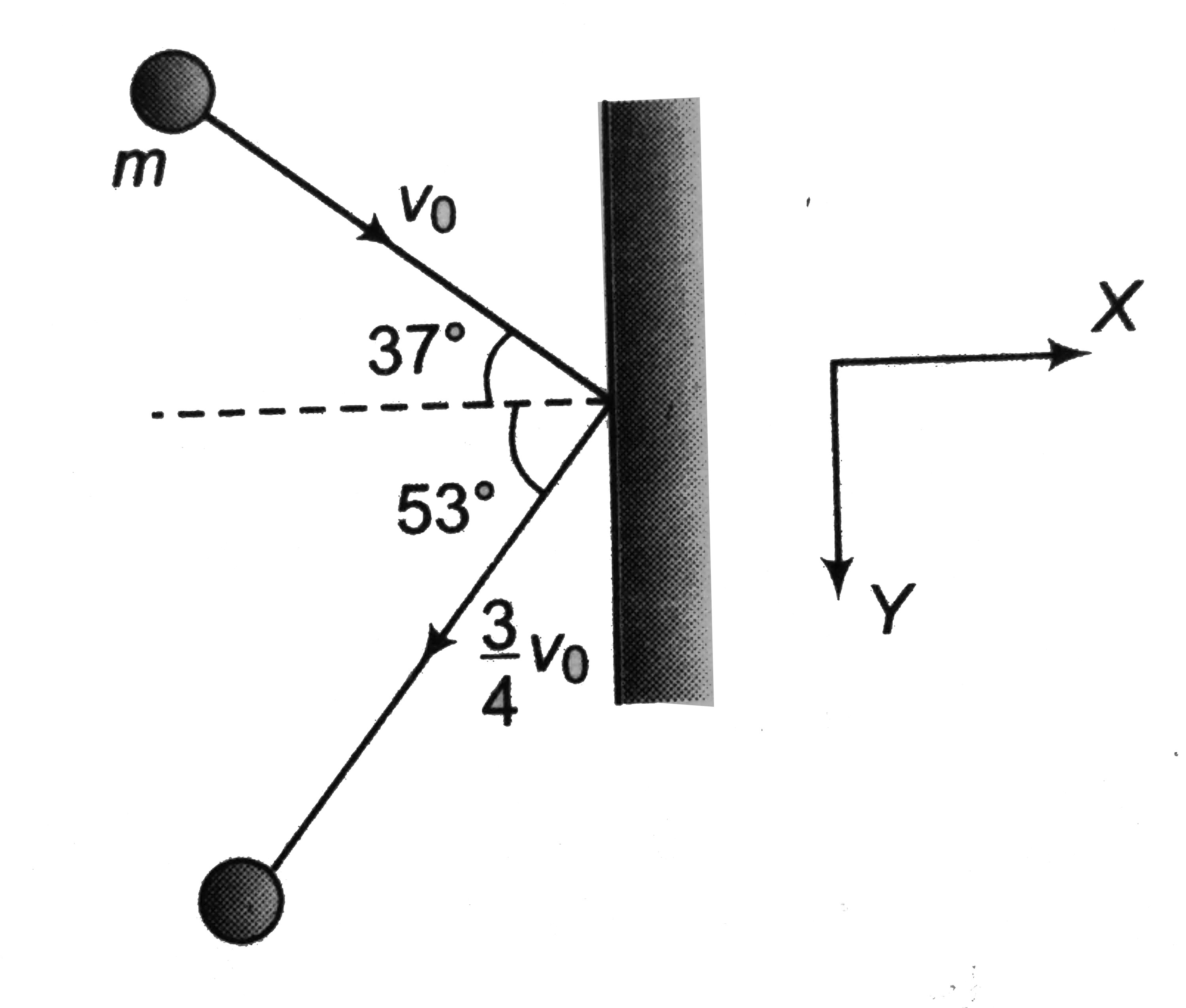
A ball of mass m moving with velocity v0 collides a wall as shown in figure. After impact it rebounds with a velocity 34v0. The impulse acting on ball during impact is
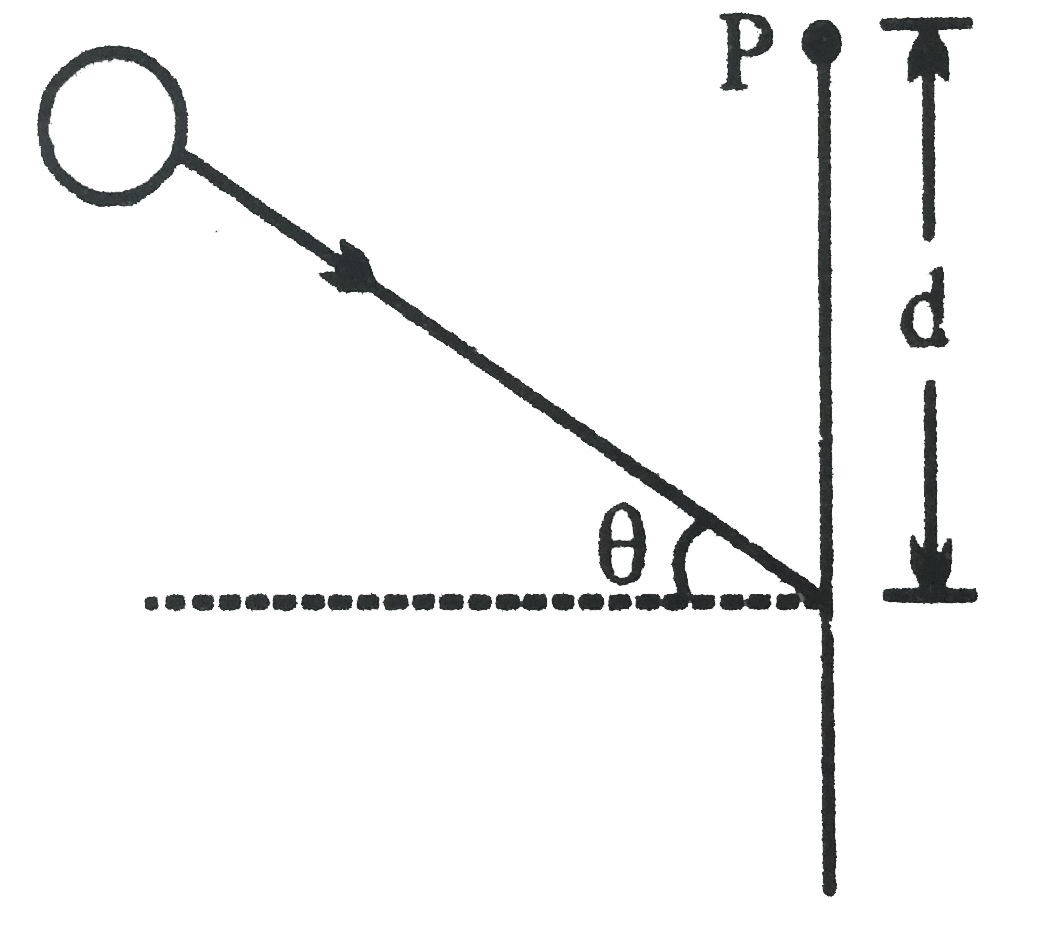
View SolutionA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
 .
.
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

View SolutionA ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball of mass m moving with velocity u collides head-on which the second ball of mass m at rest. If the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball of mass '2m' moving with velocity uˆi collides with another ball of mass 'm' moving with velocity −2uˆi. After the collision, mass 2m moves with velocity u2(ˆi−ˆj). Then the change in kinetic energy of the system ( both balls ) is
View SolutionA molecule of mass m moving at a velocity v impinges elastically on the wall at an angle α with the wall. Then
View SolutionA ball of mass 1 kg moving with a velocity of 0.4 ms−1 collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms1 in a direction making an angle of 90∘ with its initial direction. The momentum of the second ball after the collision will be (in kg ms−1)
View SolutionA ball of mass m1 is moving with velocity 3v. It collides head on elastically with a stationary ball of mass m2 . The velocity of both the balls become v after collision. Then the value of the ratio m2m1 is
View Solution
