A particle strikes a smooth horizontal surface at an angle of 45∘ with a velocity of 100m/s and rebounds. If the coefficient of restitution between the floor and the particle is 0.57 then the angle which the velocity of the particle after it rebounds will make with the floor is
30∘
45∘
60∘
90∘
Along horizontal direction
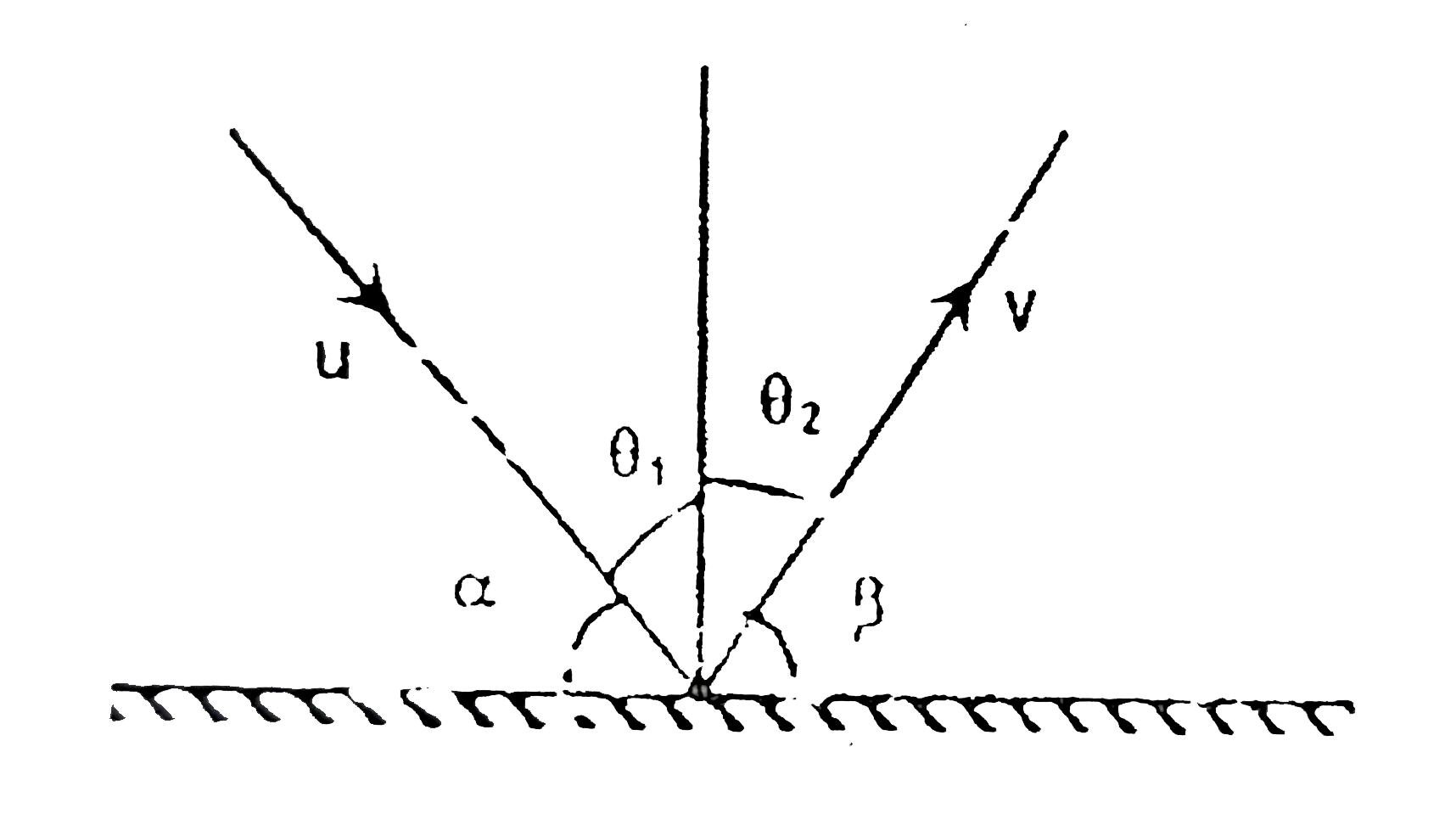
musinθ1=mvsinθ2 ……(1)
Along common normal
eucosθ1=vcosθ2……(2)
Solving Eqs. (1) and (2), θ2=tan−1(10.57tan45∘)=60∘
⇒β=30∘
Topper's Solved these Questions
Similar Questions
A particle strikes a smooth horizontal surface at an angle θ>0 and it rebounds at an angle ϕ as shown

View SolutionA particle is dropped from rest from a height h0 on a horizontal floor. The coefficient of restitution between the floor and particle is e. Maximum height attained by the particle after first rebound is
View Solution
Knowledge Check
A particle of mass, strikes on ground with angle of incidence 45∘, what will be the velocity after reflection if coefficient of restitution e=1√2
A√2v3Bv√3Cv2D√3v2A particle strikes a horizontal smooth floor with a velocity a making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. If the coefficient of restitution between the particle and the floor is e, then
Athe impulse delivered by the floor to the body is μ(1+e)sinθBtanϕ=etanθCv=u√1−(1−e)2sin2θDthe ratio of final kinetic energy to the initial kinetic energy is (cos2θ+e2sin2θ)A particle moving with a velocity of (4ˆi−ˆj ) mis strikes a fixed smooth wall and finally moves with a velocity of (3ˆi+2ˆj) m/s. The coefficient of restitution between the wall and the particle in the collision will be
A73B37C√1317D√1713
A ball strickes a horizontal floor at an angle θ=45∘ with the normal to floor. The coefficient of restitution between the ball and the floor is e=1/2. The function of its kinetic energy lost in the collision is.
View SolutionA ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball long after the collision.
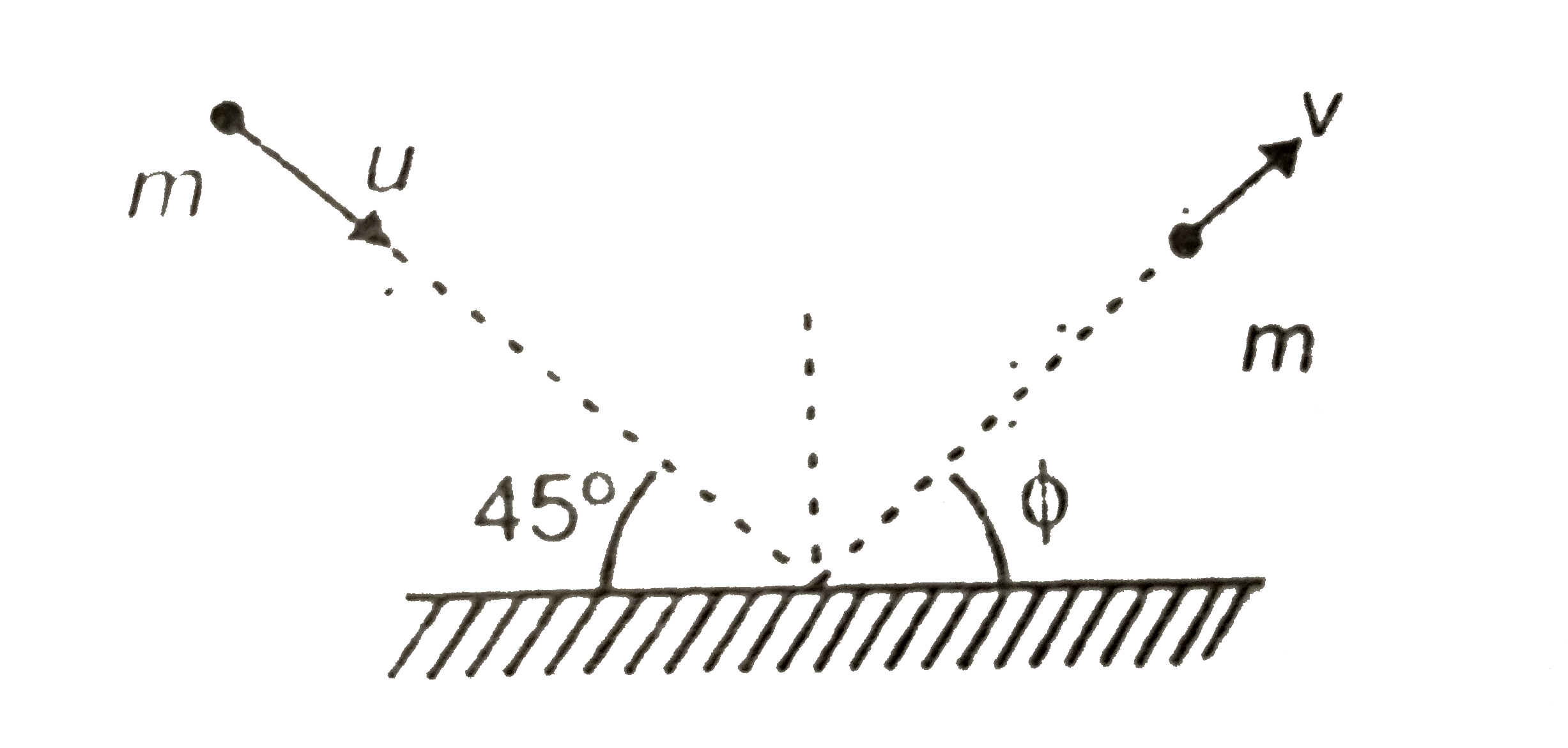
View SolutionA particle of mass m moving with a speed u strikes a smooth horizontal surface at an angle 45∘. The particle rebounds at an angle ϕ with speed v. If coefficient of restituion is 1√3, then angle ϕ is
View SolutionA steel ball strikes a fixed smooth steel plate placed on a horizontal surface at an angle θ with the vertical. If the coefficient of restitution is e, the angle at which the rebound will take place is:
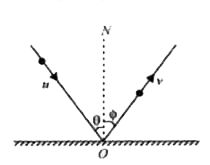
View SolutionA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The angle ϕ is equal to
View Solution

