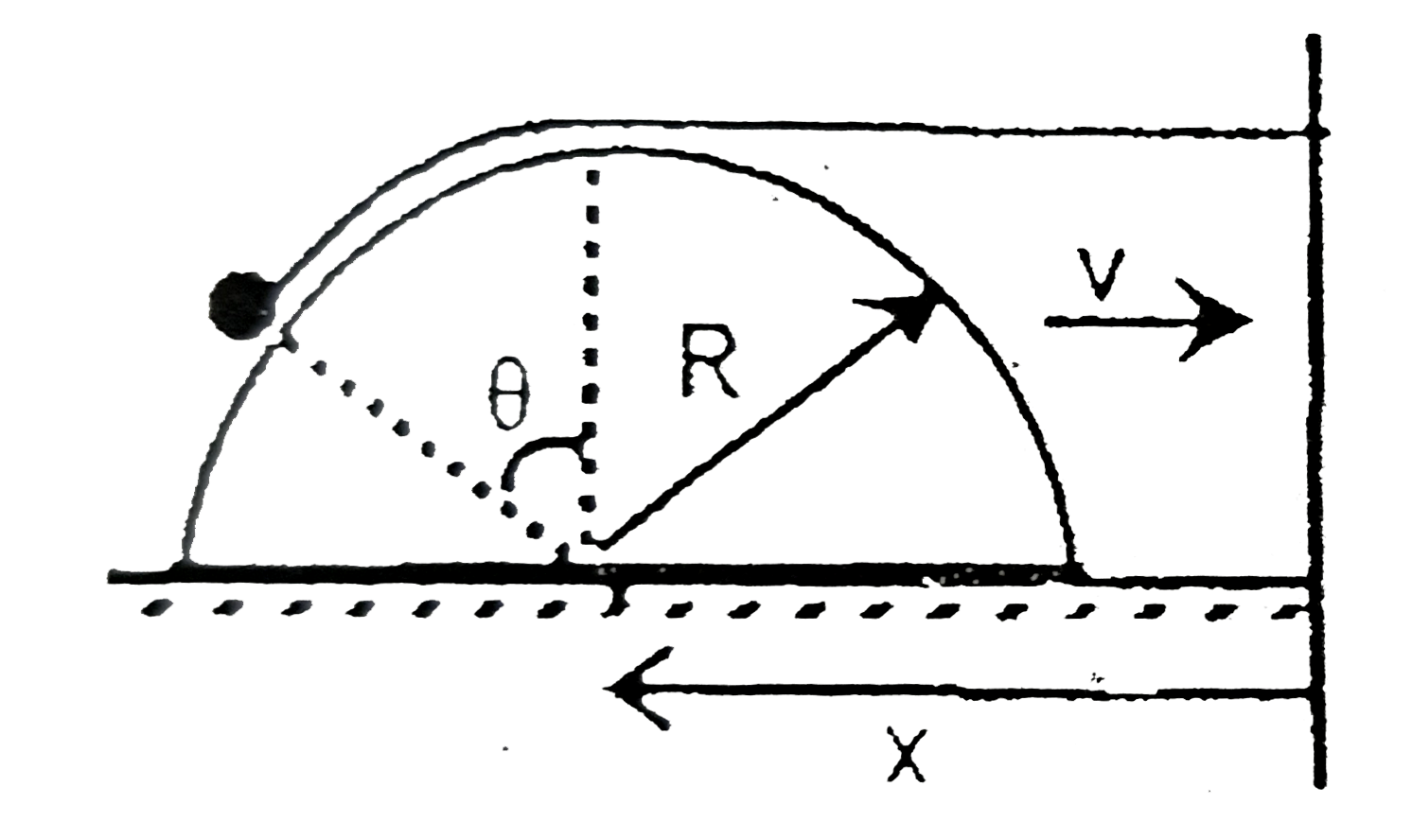
A point objects of mass m is slipping down on a smooth hemispherical body of mass M and radius R. The point object is tied to a wall with an ideal string as shown. At a certain instant, speed of the hemisphere is v and its acceleration is a. Then speed vp and acceleration ap of a particle has value (Assume all the surfaces in contact are frictionless)
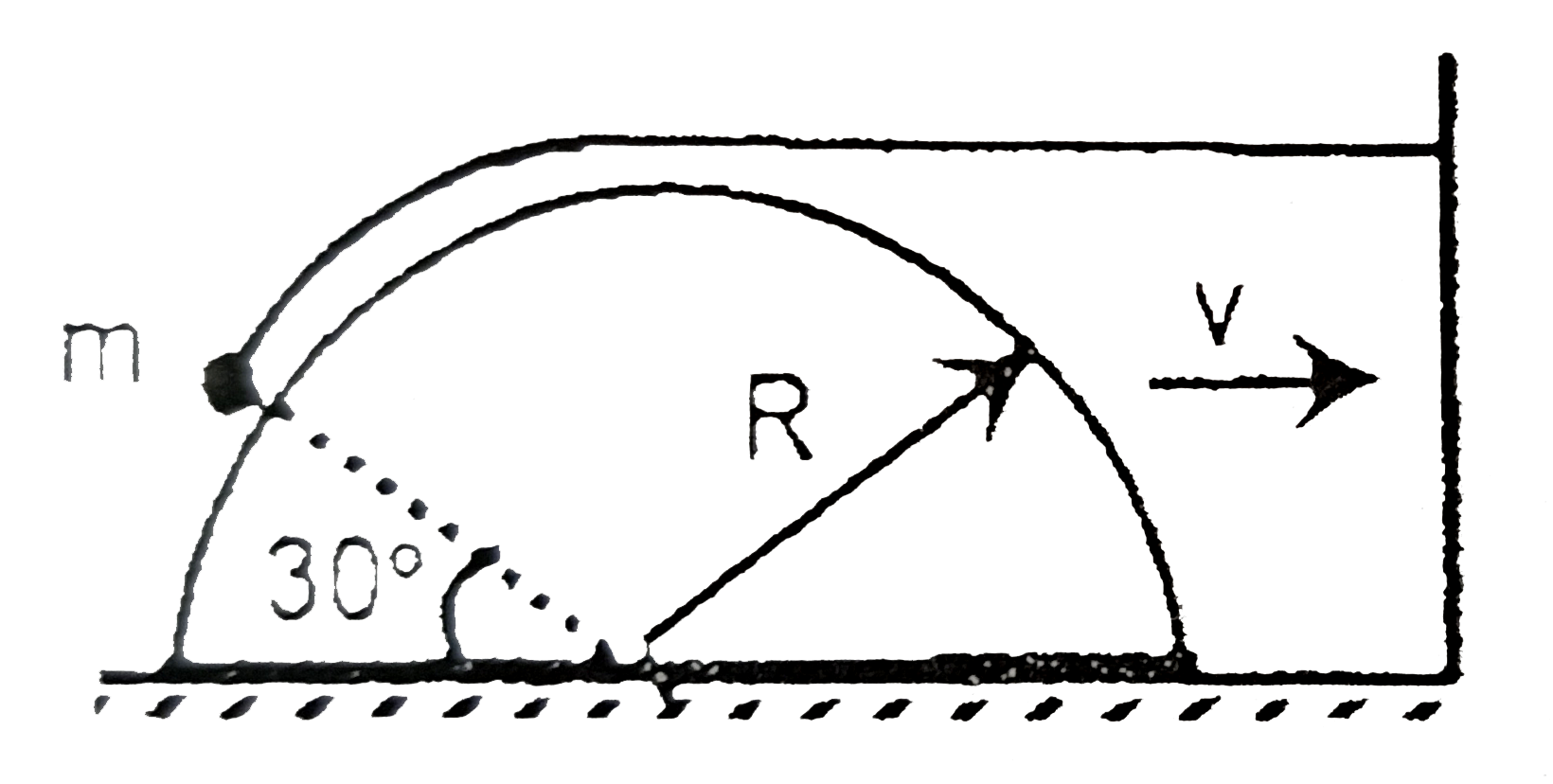
vP=vsin60∘
vP=v
aP=a
aP= ⎷[(v2R)+(a√32)]2+(a2)2
x+Rθ= constant
dxdt+Rdθdt=0
∴ω=dθdt=vR
α=dω/dt=a/R
At θ=60∘,
∴vP=v and aP=
⎷(a√32+v2R)+(a2)2
Topper's Solved these Questions
Similar Questions
An object of mass m is tied to a light string wound around a pulley that has a moment of inertia I and radius R. The wheel bearing is fricrtionless and the string does not slip on the run. Find the tension in the string and the acceleration of the object.
View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View Solution
Knowledge Check
A symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
Av/RBContinuously increasingCDependent on mass MDIndependent of radius (R)A loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
A1/2Mv2B3/2Mv2CMv2D1/2MR2ω2A particle of mass m is going along surface of smooth hemisphere of radius R in verticle plane. At the moment shown its speed is v. Choose correct option(s).
 Amg−Ncosθ=m(gsin2θ−v2Rcosθ)BN−mgcosθ=mv2RCmg−Nsinθ=mv2RDNsinθ=m(gsinθcosθ−v2Rsinθ)
Amg−Ncosθ=m(gsin2θ−v2Rcosθ)BN−mgcosθ=mv2RCmg−Nsinθ=mv2RDNsinθ=m(gsinθcosθ−v2Rsinθ)
A block of mass M is connected with a particle of mass m by a light inextensible string as shown in fig. Assuming all contaction surfaces as smooth, find the acceleration of the wedge after releasing the system.

View SolutionA car of maas M is moving on a horizontal circular path of radius r. At an instant its speed is v and is increasing at a rate a.
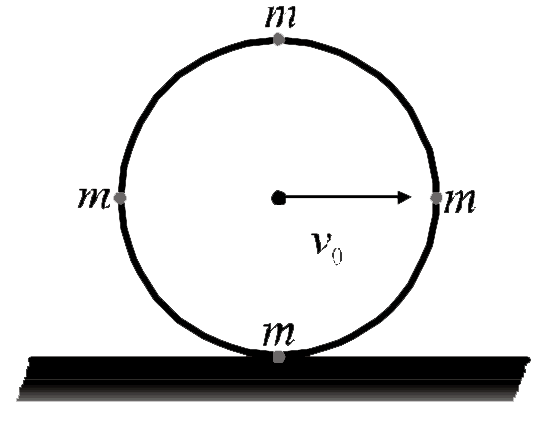
View SolutionA ring of mass m and radius R has four particles each of mass m attached to the ring as shown in figure. The centre of ring has a speed v0. The kinetic energy of the system is
View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?

View SolutionA particle of mass 'm' is moving along a circle of radius 'r'. At some instant, its speed is 'v' and it is gaining speed at a uniform rate'a', then, at the given instant, acceleration of the mparticle is :
View Solution

